Seed Phrases and Entropy

Warning: This post has KaTeX enabled, so if you want to view the rendered math formulas, you’ll have to unfortunately enable JavaScript.

In this post, let’s dive into a topic that is very important for anyone who uses the internet: passwords. We’ll cover what the hell is Entropy, good password practices, and how it relates to Bitcoin “seed phrases”¹.

Entropy

Before we go into passwords, I’ll introduce the concept of Entropy.

Entropy is a measure of the amount of disorder in a system. It has its origins in Thermodynamics, where it’s used to measure the amount of energy in a system that is not available to do work.

The etymology of the word “Entropy” is after the Greek word for “transformation”.

It was given a proper statistical definition by Ludwig Boltzmann in 1870s. while establishing the field of Statistical Dynamics, a field of physics that studies the behavior of large collections of particles.

In the context of Statistical Dynamics, Entropy is a measure of the number of ways a system can be arranged. The more ways a system can be arranged, the higher its Entropy. Specifically, Entropy is a logarithmic measure of the number of system states with significant probability of being occupied:

$$S = -k \cdot \sum_i p_i \ln p_i$$

Where:

• $S$: Entropy.
• $k$: Boltzmann’s constant, a physical constant that relates temperature to energy.
• $p_i$: probability of the system being in state $i$.

In this formula, if all states are equally likely, i.e $p_i = \frac{1}{N}$, where $N$ is the number of states, then the entropy is maximized. You can see this since a probability $p$ is a real number between 0 and 1, and as $N$ approaches infinity, the sum of the logarithms approaches negative infinity. Then, multiplying by $-k$ yields positive infinity.

How the hell Physics came to Passwords?

There’s once a great men called Claude Shannon, who single-handedly founded the field of Information Theory, invented the concept of a Bit, and was the first to think about Boolean algebra in the context of electrical circuits. He laid the foundation for the Digital Revolution.

If you are happy using your smartphone, laptop, or any other digital device, in you high speed fiber internet connection, through a wireless router to send cats pictures to your friends, then you should thank Claude Shannon.

He was trying to find a formula to quantify the amount of information in a message. He wanted three things:

1. The measure should be a function of the probability of the message. Messages that are more likely should have less information.
2. The measure should be additive. The information in a message should be the sum of the information in its parts.
3. The measure should be continuous. Small changes in the message should result in small changes in the measure.

He pretty much found that the formula for Entropy in statistical mechanics was a good measure of information. He called it Entropy to honor Boltzmann’s work. To differentiate it from the Statistical Dynamics’ Entropy, he changed the letter to $H$, in honor of Boltzmann’s $H$-theorem. So the formula for the Entropy of a message is:

$$H(X) = −\Sigma_{x \in X} P(x_i​) \log ​P(x_i​)$$

Where:

• $X$: random discrete variable.
• $H(X)$: Entropy of $X$
• $P(x_i)$: probability of the random variable $X$ taking the value $x_i$. Also known as the probability mass function (PMF) of the discrete random variable $X$.
• $\log$: base 2 logarithm, to measure the Entropy in bits.

In information theory, the Entropy of a random variable is the average level of “information”, “surprise”, or “uncertainty” inherent to the variable’s possible outcomes².

Let’s take the simple example of a fair coin. The Entropy of the random variable $X$ that represents the outcome of a fair coin flip is:

$$H(X) = −\Sigma_{x \in X} P(x_i​) \log ​P(x_i​) = -\left(\frac{1}{2} \log \frac{1}{2} + \frac{1}{2} \log \frac{1}{2}\right) = 1 \text{ bit}$$

So the outcome of a fair coin flip has 1 bit of Entropy. This means that the outcome of a fair coin flip has 1 bit of information, or 1 bit of uncertainty. Once the message is received, that the coin flip was heads or tails, the receiver has 1 bit of information about the outcome.

Alternatively, we only need 1 bit to encode the outcome of a fair coin flip. Hence, there’s a connection between Entropy, search space, and information.

Another good example is the outcome of a fair 6-sided die. The Entropy of the random variable $X$ that represents the outcome of a fair 6-sided die is:

$$H(X) = −\Sigma_{x \in X} P(x_i​) \log ​P(x_i​) = - \sum_{i=1}^6\left(\frac{1}{6} * \log \frac{1}{6} \right) \approx 2.58 \text{ bits}$$

This means that the outcome of a fair 6-sided die has 2.58 bits of Entropy. we need $\operatorname{ceil}(2.58) = 3$ bits to encode the outcome of a fair 6-sided die.

Entropy and Passwords

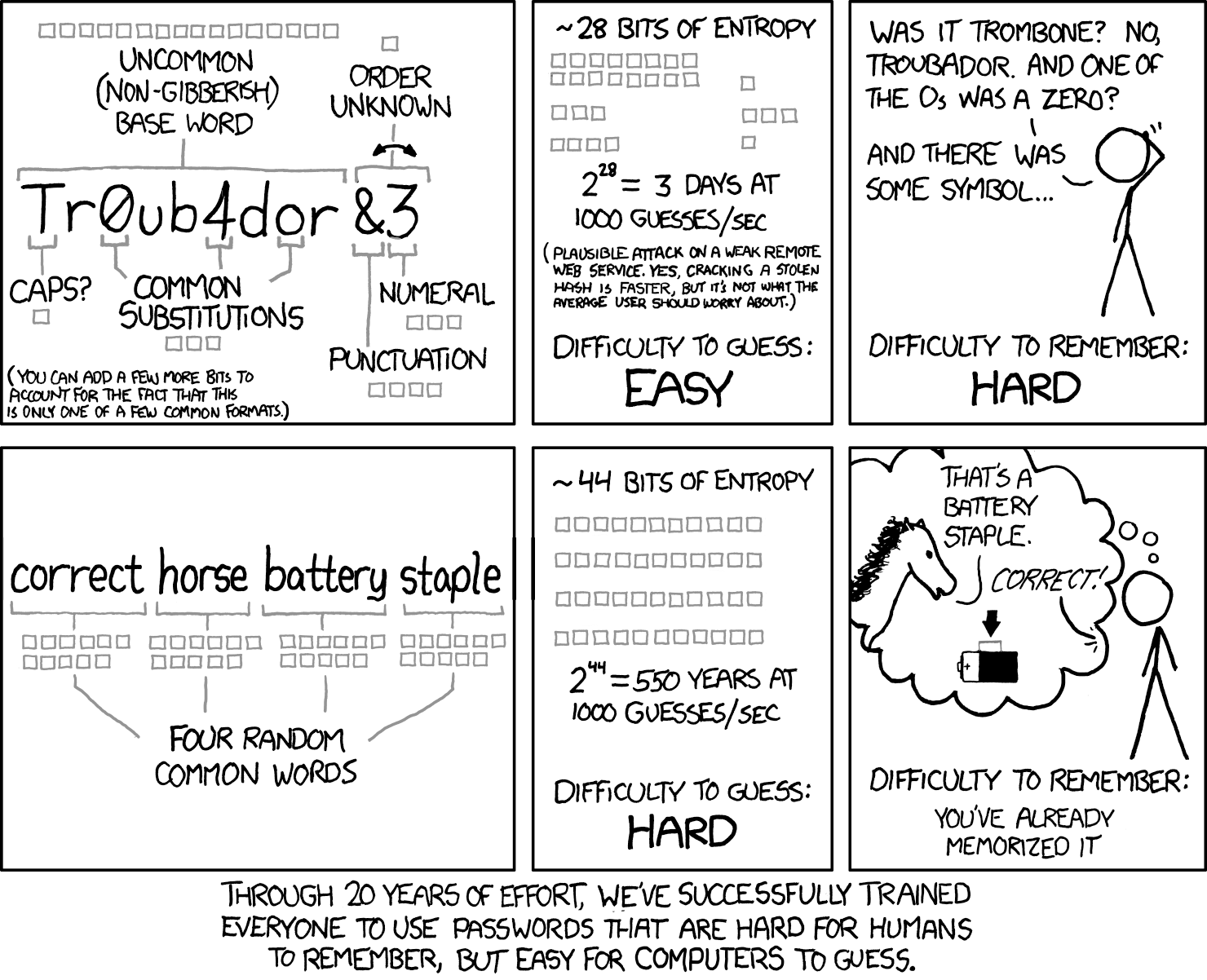
Ok now we come full circle. Let’s talk, finally, about passwords.

In the context of passwords, Entropy is a measure of how unpredictable a password is. The higher the Entropy, the harder it is to guess the password. The Entropy of a password is measured in bits, and it’s calculated using the formula:

$$H = L \cdot \log_2(N)$$

Where:

• $H$: Entropy in bits
• $N$: number of possible characters in the password
• $L$: length of the password
• $\log_2$:​ (N) calculates how many bits are needed to represent each character from the set.

For example, if we have a password with 8 characters and each character can be any of the 26 lowercase letters, the standard english alphabet, the Entropy would be:

$$H = 8 \cdot \log_2(26) \approx 37.6 \text{ bits}$$

This means that an attacker would need to try $2^{37.6} \approx 2.01 \cdot 10^{11}$ combinations³ to guess the password.

If the password were to include uppercase letters, numbers, and symbols (let’s assume 95 possible characters in total), the Entropy for an 8-character password would be:

$$H = 8 \cdot \log_2(95) \approx 52.6 \text{ bits}$$

This means that an attacker would need to try $2^{52.6} \approx 6.8 \cdot 10^{15}$ combinations to guess the password.

This sounds a lot but it’s not that much.

For the calculations below, we’ll assume that the attacker now your dictionary set, i.e. the set of characters you use to create your password, and the password length.

If an attacker get a hold of an NVIDIA RTX 4090, MSRP USD 1,599, which can do 300 GH/s (300,000,000,000 hashes/second), i.e. $3 \cdot 10^{11}$ hashes/second, it would take:

1. 8-length lowercase-only password:

$$\frac{2.01 \cdot 10^{11}}{3 \cdot 10^{11}} \approx 0.67 \text{ seconds}$$

1. 8-length password with uppercase letters, numbers, and symbols:

$$\frac{6.8 \cdot 10^{15}}{3 \cdot 10^{11}} \approx 22114 \text{ seconds} \approx 6.14 \text{ hours}$$

So, the first password would be cracked in less than a second, while the second would take a few hours. This with just one 1.5k USD GPU.

Bitcoin Seed Phrases

Now that we understand Entropy and how it relates to passwords, let’s talk about bitcoin seed phrases¹.

Remember that our private key is a big-fucking number? If not, check my post on cryptographics basics.

BIP-39 specifies how to use easy-to-remember seed phrases to store and recover private keys. The wordlist adheres to the following principles:

1. smart selection of words: the wordlist is created in such a way that it’s enough to type the first four letters to unambiguously identify the word.
2. similar words avoided: word pairs like “build” and “built”, “woman” and “women”, or “quick” and “quickly” not only make remembering the sentence difficult but are also more error prone and more difficult to guess.

Here is a simple 7-word seed phrase: brave sadness grocery churn wet mammal tube. Surprisingly enough, this badboy here gives you $77$ bits of Entropy, while also being easy to remember. This is due to the fact that the wordlist has 2048 words, so each word gives you $\log_2(2048) = 11$ bits of Entropy⁴.

There’s a minor caveat to cover here. The last word in the seed phrase is a checksum, which is used to verify that the phrase is valid.

So, if you have a 12-word seed phrase, you have $11 \cdot 11 = 121$ bits of Entropy. And for a 24-word seed phrase, you have $23 \cdot 11 = 253$ bits of Entropy.

The National Institute of Standards and Technology (NIST) recommends a minimum of 112 bits of Entropy for all things cryptographic. And Bitcoin has a minimum of 128 bits of Entropy.

Depending on your threat model, “Assume that your adversary is capable of a trillion guesses per second”, it can take a few years to crack a 121-bit Entropy seed phrase:

$$\frac{2^{121}}{10^{12}} \approx 2.66 \cdot 10^{24} \text{ seconds} \approx 3.08 \cdot 10^{19} \text{ days} \approx 8.43 \cdot 10^{16} \text{ years}$$

That’s a lot of years. Now for a 253-bit Entropy seed phrase:

$$\frac{2^{253}}{10^{12}} \approx 1.45 \cdot 10^{64} \text{ seconds} \approx 1.68 \cdot 10^{59} \text{ days} \approx 4.59 \cdot 10^{56} \text{ years}$$

That’s another huge number of years.

Seed Phrases and Passwords

You can also use a seed phrase as a password. The bonus point is that you don’t need to use the last word as a checksum, so you get 11 bits of Entropy free, compared to a Bitcoin seed phrase.

Remember the 7-words badboy seed phrase we generated earlier? brave sadness grocery churn wet mammal tube.

It has $66$ bits of Entropy. This would take, assuming “that your adversary is capable of a trillion guesses per second”:

$$\frac{2^{77}}{10^{12}} \approx 1.51 \cdot 10^{11} \text{ seconds} \approx 1.75 \cdot 10^{6} \text{ days} \approx 4.79 \cdot 10^{3} \text{ years}$$

That’s why tons of people use seed phrases as passwords. Even if you know the dictionary set and the length of the password, i.e. the number of words in the seed phrase, it would take a lot of years to crack it.

Conclusion

Entropy is a measure of the amount of disorder in a system. In the context of passwords, it’s a measure of how unpredictable a password is. The higher the Entropy, the harder it is to guess the password.

Bitcoin seed phrases are a great way to store and recover private keys. They are easy to remember and have a high amount of Entropy. You can even use a seed phrase as a password.

Even it your attacker is capable of a trillion guesses per second, like the NSA, it would take them a lot of years to crack even a 7-word seed phrase.

If you want to generate a seed phrase, you can use KeePassXC, which is a great open-source offline password manager that supports seed phrases⁵.

License

This post is licensed under Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International.