Markov Chain Monte Carlo – MCMC

O motor por trás da Estatística Bayesiana

A principal barreira computacional para estatística Bayesiana é o denominador \(P(\text{data})\) da fórmula de Bayes:

\[P(\theta \mid \text{data})=\frac{P(\theta) \cdot P(\text{data} \mid \theta)}{P(\text{data})}\]

Em casos discretos podemos fazer o denominador virar a soma de todos os parâmetros usando a regra da cadeia de probabilidade:

\[P(A,B \mid C)=P(A \mid B,C) \times P(B \mid C)\]

Isto também é chamado de marginalização:

\[P(\text{data})=\sum_{\theta} P(\text{data} \mid \theta) \times P(\theta)\]

Porém no caso de valores contínuos o denominador \(P(\text{data})\) vira uma integral bem grande e complicada de calcular:

\[P(\text{data})=\int_{\theta} P(\text{data} \mid \theta) \times P(\theta)d \theta\]

Em muitos casos essa integral vira intratável (incalculável) e portanto devemos achar outras maneiras de calcular a probabilidade posterior \(P(\theta \mid \text{data})\) de Bayes sem usar o denominador \(P(\text{data})\).

Para quê serve o denominador \(P(\text{data})\)?

Para normalizar a posterior com o intuito de torná-la uma distribuição probabilística válida. Isto quer dizer que a soma de todas as probabilidades dos eventos possíveis da distribuição probabilística devem ser iguais a 1:

• no caso de distribuição probabilística discreta: \(\sum_{\theta} P(\theta \mid \text{data}) = 1\)
• no caso de distribuição probabilística contínua: \(\int_{\theta} P(\theta \mid \text{data})d \theta = 1\)

Se removermos o denominador de Bayes o que temos?

Ao removermos o denominador \((\text{data})\) temos que a posterior \(P(\theta \mid \text{data})\) é proporcional à prior multiplicada pela verossimilhança \(P(\theta) \cdot P(\text{data} \mid \theta)\)¹.

\[P(\theta \mid \text{data}) \propto P(\theta) \cdot P(\text{data} \mid \theta)\]

Este vídeo do YouTube explica muito bem o problema do denominador.

Simulação Montecarlo com correntes Markov – (MCMC)

Aí que entra simulação Montecarlo com correntes Markov (do inglês Markov Chain Monte Carlo – MCMC). MCMC é uma classe ampla de ferramentas computacionais para aproximação de integrais e geração de amostras de uma probabilidade posterior (S. Brooks, Gelman, Jones, & Meng, 2011). MCMC é usada quando não é possível coletar amostras de \(\boldsymbol{\theta}\) direto da distribuição probabilística posterior \(P(\boldsymbol{\theta} \mid \text{data})\). Ao invés disso, nos coletamos amostras de maneira iterativa que a cada passo do processo nós esperamos que a distribuição da qual amostramos \(P^*(\boldsymbol{\theta}^{(*)} \mid \text{data})\) (aqui \(*\) quer dizer simulado) se torna cada vez mais similar à posterior \(P(\boldsymbol{\theta} \mid \text{data})\). Tudo isso é para eliminar o cálculo (muitas vezes impossível) do denominador \(P(\text{data})\).

A ideia é definir uma corrente Markov ergódica (quer dizer que há uma distribuição estacionária única) dos quais o conjunto de estados possíveis é o espaço amostral e a distribuição estacionária é a distribuição a ser aproximada (ou amostrada). Seja \(X_0, X_1, \dots, X_n\) uma simulação da corrente. A corrente Markov converge à distribuição estacionária de qualquer estado inicial \(X_0\) após um número suficiente grande de iterações \(r\), a distribuição do estado \(X_r\) estará similar à distribuição estacionária, então podemos usá-la com amostra. As correntes Markov possuem uma propriedade que a distribuição de probabilidade do próximo estado depende apenas do estado atual e não na sequência de eventos que precederam: \(P(X_{n+1}=x \mid X_{0},X_{1},X_{2},\ldots ,X_{n}) = P(X_{n+1}=x \mid X_{n})\). Essa propriedade é chamada de Markoviana, em homenagem ao matemático Andrei Andreyevich Markov (figura 1). Similarmente, repetindo esse argumento com \(X_r\) como o ponto inicial, podemos usar \(X_{2r}\) como amostra, e assim por diante. Podemos então usar a sequência de estados \(X_r, X_{2r}, X_{3r}, \dots\) como quase amostras independentes da distribuição estacionária da corrente Markov.

Figure 1: Andrei Andreyevich Markov. Figura de https://www.wikipedia.org

A eficácia dessa abordagem depende em:

1. o quão grande \(r\) deve ser para garantir uma amostra adequadamente boa; e

2. poder computacional requerido para cada iteração da corrente Markov.

Além disso, é costumeiro descartarmos as primeiras iterações do algoritmo pois elas costumam não ser representativas da distribuição a ser aproximada. Nas iterações iniciais de algoritmos MCMC geralmente a corrente Markov está em um processo de aquecimento² (warm-up) e seu estado está bem distante do ideal para começarmos uma amostragem fidedigna. Geralmente, recomenda-se que se descarte metade das iterações (Gelman et al., 2013a). Por exemplo: se a corrente Markov possui 4.000 iterações, descartamos as 2.000 primeiras como warm-up.

Método Monte Carlo

Stanislaw Ulam (figura 2), que participou do projeto Manhattan e ao tentar calcular o processo de difusão de neutrons para a bomba de hidrogênio acabou criando uma classe de métodos chamada Monte Carlo.

Figure 2: Stanislaw Ulam. Figura de https://www.wikipedia.org

Métodos de Monte Carlo possuem como conceito subjacente o uso a aleatoriedade para resolver problemas que podem ser determinísticos em princípio. Eles são freqüentemente usados em problemas físicos e matemáticos e são mais úteis quando é difícil ou impossível usar outras abordagens. Os métodos de Monte Carlo são usados principalmente em três classes de problemas: otimização, integração numérica e geração de sorteios a partir de uma distribuição de probabilidade.

A ideia do método veio enquanto jogava paciência durante sua recuperação de uma cirurgia, Ulam pensou em jogar centenas de jogos para estimar estatisticamente a probabilidade de um resultado bem-sucedido. Conforme ele mesmo menciona em Eckhardt (1987):

Os primeiros pensamentos e tentativas que fiz para praticar [o Método de Monte Carlo] foram sugeridos por uma pergunta que me ocorreu em 1946 quando eu estava convalescendo de uma doença e jogando paciência. A questão era quais são as chances de que um jogo de paciência com 52 cartas obtivesse sucesso? Depois de passar muito tempo tentando estimá-los por meio de cálculos combinatórios puros, me perguntei se um método mais prático do que o “pensamento abstrato” não seria expô-lo, digamos, cem vezes e simplesmente observar e contar o número de jogadas bem-sucedidas. Isso já era possível imaginar com o início da nova era de computadores rápidos, e eu imediatamente pensei em problemas de difusão de nêutrons e outras questões de física matemática e, de forma mais geral, como mudar os processos descritos por certas equações diferenciais em uma forma equivalente interpretável como uma sucessão de operações aleatórias. Mais tarde [em 1946], descrevi a ideia para John von Neumann e começamos a planejar cálculos reais.

Por ser secreto, o trabalho de von Neumann e Ulam exigia um codinome. Um colega de von Neumann e Ulam, Nicholas Metropolis (figura 5), sugeriu usar o nome Monte Carlo, que se refere ao Casino Monte Carlo em Mônaco, onde o tio de Ulam (Michał Ulam) pedia dinheiro emprestado a parentes para jogar.

As aplicações do método de Monte Carlo são inúmeras: ciências físicas, engenharia, mudança climática, biologia computacional, computação gráfica, estatística aplicada, inteligência artificial, design e recursos visuais, busca e resgate, finanças e negócios e direito. No escopo desta aula focaremos em estatística aplicada e especificamente no contexto de inferência Bayesiana: fornecer uma amostra aleatória da distribuição posterior.

Simulações – Setup

Estou usando diversos pacotes:

• ggplot2, plotly e ggforce para gráficos.

• gganimate para animações (GIFs).

• MASS para simulações aleatórias de distribuições multivariadas.

• rstan para funções de sumário e métricas de convergência e desempenho de simulações MCMC.

library(ggplot2)
theme_set(theme_minimal())
library(plotly)
library(gganimate)
library(ggforce)
library(MASS)
library(rstan)

Vamos começar com um problema didático de uma distribuição normal multivariada de \(X\) e \(Y\), onde

\[ \begin{bmatrix} X \\ Y \end{bmatrix} \sim \text{Normal Multivariada} \left( \begin{bmatrix} \mu_X \\ \mu_Y \end{bmatrix}, \mathbf{\Sigma} \right) \\ \mathbf{\Sigma} \sim \begin{pmatrix} \sigma^2_{X} & \sigma_{X}\sigma_{Y} \rho \\ \sigma_{X}\sigma_{Y} \rho & \sigma^2_{Y} \end{pmatrix} \]

Se designarmos \(\mu_X = \mu_Y = 0\) e \(\sigma_X = \sigma_Y = 1\) (média 0 e desvio padrão 1 para ambos \(X\) e \(Y\)), temos a seguinte formulação:

\[ \begin{bmatrix} X \\ Y \end{bmatrix} \sim \text{Normal Multivariada} \left( \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \mathbf{\Sigma} \right), \\ \mathbf{\Sigma} \sim \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix}. \]

Só faltando designar um valor de \(\rho\) para a correlação entre \(X\) e \(Y\). Para o nosso exemplo vamos usar correlação de 0.8 (\(\rho = 0.8\)):

\[ \mathbf{\Sigma} \sim \begin{pmatrix} 1 & 0.8 \\ 0.8 & 1 \end{pmatrix}. \]

N <- 1e5
mus  <- c(0, 0)
sigmas <- c(1, 1)
r <- 0.8
Sigma <- diag(sigmas)
Sigma[1, 2] <- r
Sigma[2, 1] <- r
dft <- data.frame(mvrnorm(N, mus, Sigma))

Na figura 3 é possível ver um gráfico de densidade de uma distribuição multivariada normal de duas variáveis normais \(X\) e \(Y\), ambas com média 0 e desvio padrão 1. Sendo que a correlação entre elas é 0.8. E na figura 4 é possível ver uma imagem 3-D interativa da mesma distribuição, fique a vontade em usar seu mouse (dedo ou caneta, dependendo do dispositivo) para movimentar a imagem.

ggplot(dft, aes(X1, X2)) +
  geom_density2d_filled() +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(title = "Multivariada Normal",
       subtitle = expression(list(mu == 0, sigma == 1, rho == 0.8)),
       caption = "10.000 simulações",
       x = expression(X), y = expression(Y)) +
  theme(legend.position = "NULL")

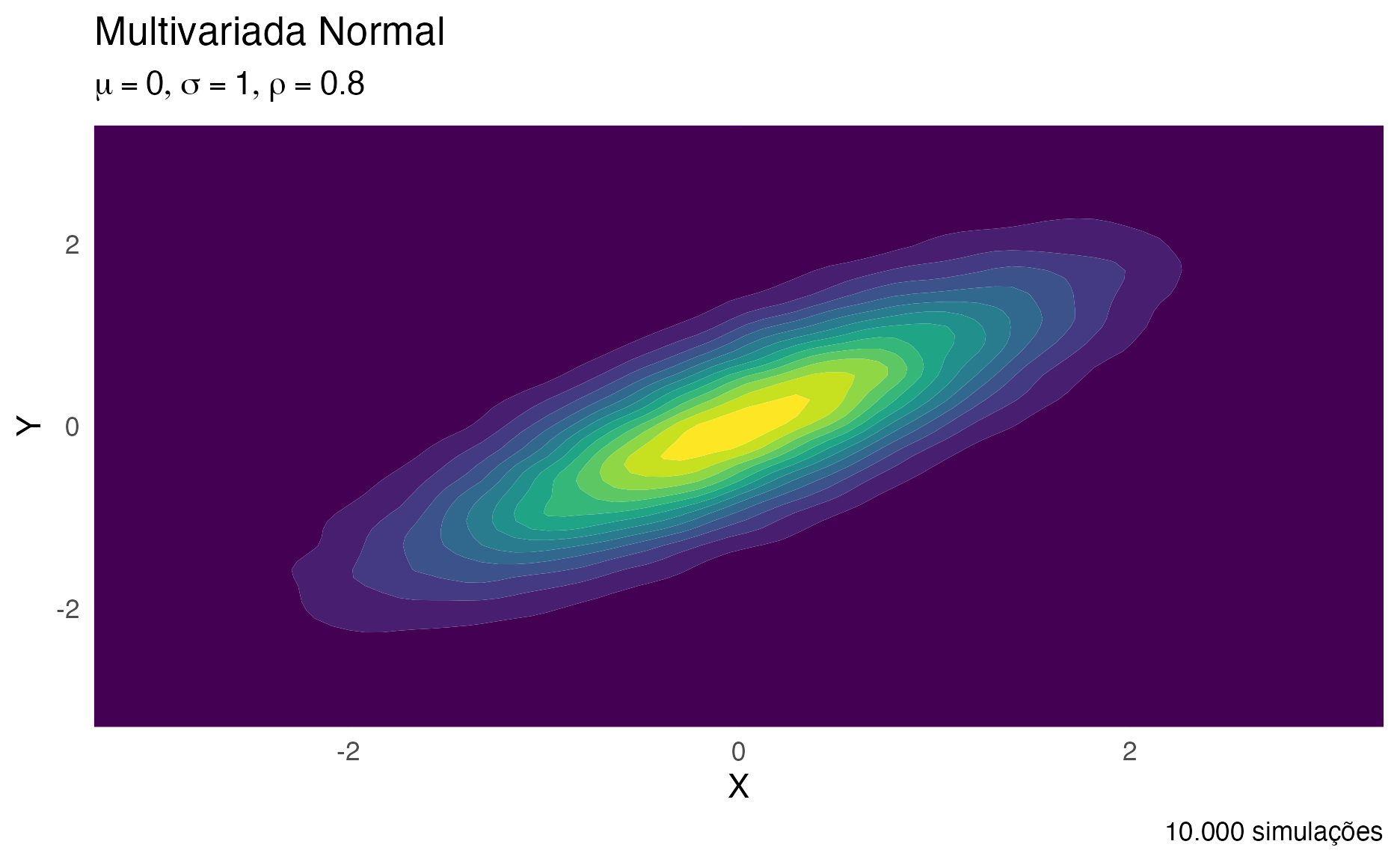
Figure 3: Gráfico de Densidade de uma distribuição Multivariada Normal

dens <- kde2d(dft$X1, dft$X2)
plot_ly(x = dens$x,
        y = dens$y,
        z = dens$z) %>% add_surface()

Figure 4: Imagem 3-D Interativa de uma distribuição Multivariada Normal

Metropolis e Metropolis-Hastings

O primeiro algoritmo MCMC amplamente utilizado para gerar amostras de correntes Markov foi originário na física na década de 1950 (inclusive uma relação muito próxima com a bomba atômica no projeto Manhattan) e chama-se Metropolis (Metropolis, Rosenbluth, Rosenbluth, Teller, & Teller, 1953) em homenagem ao primeiro autor Nicholas Metropolis (figura 5). Em síntese, o algoritmo de Metropolis é uma adaptação de um passeio aleatório (random walk) com uma regra de aceitação/rejeição para convergir à distribuição-alvo.

O algorimo de Metropolis usa uma distribuição de propostas \(J_t(\boldsymbol{\theta}^{(*)})\) (\(J\) quer dizer jumping distribution e \(t\) indica em qual estado da corrente Markov estamos) para definir próximos valores da distribuição \(P^*(\boldsymbol{\theta}^{(*)} \mid \text{data})\). Essa distribuição deve ser simétrica:

\[ J_t (\boldsymbol{\theta}^{(*)} \mid \boldsymbol{\theta}^{(t-1)}) = J_t(\boldsymbol{\theta}^{(t-1)} \mid \boldsymbol{\theta}^{(*)}). \]

Na década de 1970, surgiu um generalização do algoritmo de Metropolis que não necessita que as distribuições de proposta sejam simétricas. A generalização foi proposta por Wilfred Keith Hastings (Hastings, 1970) (figura 5) e chama-se algoritmo de Metropolis-Hastings.

Figure 5: Da esquerda para direita: Nicholas Metropolis e Wilfred Hastings – Figuras de https://www.wikipedia.org

Algoritmo de Metropolis

A essência do algoritmo é um passeio aleatório (random walk) pelo espaço amostral dos parâmetros, onde a probabilidade da corrente Markov mudar de estado é definida como:

\[ P_{\text{mudar}} = \min\left({\frac{P (\boldsymbol{\theta}_{\text{proposto}})}{P (\boldsymbol{\theta}_{\text{atual}})}},1\right). \]

Isso quer dizer a corrente Markov somente mudará para um novo estado em duas condições:

1. Quando a probabilidade dos parâmetros propostos pelo passeio aleatório \(P(\boldsymbol{\theta}_{\text{proposto}})\) é maior que a probabilidade dos parâmetros do estado atual \(P(\boldsymbol{\theta}_{\text{atual}})\), mudamos com 100% de probabilidade. Vejam que se \(P(\boldsymbol{\theta}_{\text{proposto}}) > P(\boldsymbol{\theta}_{\text{atual}})\) então a função \(\min\) escolhe o valor 1 que quer dizer 100%.
2. Quando a probabilidade dos parâmetros propostos pelo passeio aleatório \(P(\boldsymbol{\theta}_{\text{proposto}})\) é menor que a probabilidade dos parâmetros do estado atual \(P(\boldsymbol{\theta}_{\text{atual}})\), mudamos com probabilidade igual a proporção dessa diferença. Vejam que se \(P(\boldsymbol{\theta}_{\text{proposto}}) < P(\boldsymbol{\theta}_{\text{atual}})\) então a função \(\min\) não escolhe o valor 1, mas sim o valor \(\frac{P (\boldsymbol{\theta}_{\text{proposto}})}{P (\boldsymbol{\theta}_{\text{atual}})}\) que equivale a proporção da probabilidade dos parâmetros propostos pela probabilidade dos parâmetros do estado atual.

De qualquer maneira, a cada iteração do algoritmo de Metropolis, mesmo que a corrente muda de estado ou não, amostramos o parâmetro \(\boldsymbol{\theta}\) de qualquer maneira. Ou seja, se a corrente não mudar em um certo estado \(\boldsymbol{\theta}\) será amostrado duas vezes (ou mais caso a corrente fique estacionária no mesmo estado).

O algoritmo de Metropolis-Hastings pode ser descrito na seguinte maneira³ (\(\boldsymbol{\theta}\) é o parâmetro, ou conjunto de parâmetros, de interesse e \(y\) são os dados):

1. Defina um ponto inicial \(\boldsymbol{\theta}^{(0)} \in \mathbb{R}^p\) do qual \(P\left(\boldsymbol{\theta}^{(0)} \mid y \right) > 0\), ou amostre-o de uma distribuição inicial \(P_0 (\boldsymbol{\theta})\). \(P_0(\boldsymbol{\theta})\) pode ser uma distribuição normal ou uma distribuição prévia de \(\boldsymbol{\theta}\) (\(P(\boldsymbol{\theta})\)).

2. Para \(t = 1, 2, \dots\):

   • Amostra uma proposta \(\boldsymbol{\theta}^{(*)}\) de uma distribuição de propostas no tempo \(t\), \(J_t \left(\boldsymbol{\theta}^{(*)} \mid \boldsymbol{\theta}^{(t-1)} \right)\)

   • Como regra de aceitação/rejeição calcule a proporção das probabilidades:

     • Metropolis: \(r = \frac{P\left(\boldsymbol{\theta}^{(*)} \mid y \right)}{P\left(\boldsymbol{\theta}^{(t-1)} \mid y \right)}\)
     • Metropolis-Hastings: \(r = \frac{\frac{P \left(\boldsymbol{\theta}^{(*)} \mid y \right)}{J_t \left(\boldsymbol{\theta}^{(*)} \mid \boldsymbol{\theta}^{(t-1)} \right)}}{\frac{P \left(\boldsymbol{\theta}^{(t-1)} \mid y \right)}{J_t \left(\boldsymbol{\theta}^{(t-1)} \mid \boldsymbol{\theta}^{(*)} \right)}}\)

   • Designe:

     \[\boldsymbol{\theta}^{(t)} = \begin{cases} \boldsymbol{\theta}^{(*)} & \text{com probabilidade $\min(r,1)$}\\ \boldsymbol{\theta}^{(t-1)} & \text{caso contrário} \end{cases}\]

Limitações do Algoritmo de Metropolis

As limitações do algoritmo de Metropolis-Hastings são principalmente computacionais. Com propostas geradas aleatoriamente, geralmente leva um grande número de iterações para entrar em áreas de densidade posterior mais alta (mais provável). Mesmo algoritmos de Metropolis-Hastings eficientes às vezes aceitam menos de 25% das propostas (Beskos, Pillai, Roberts, Sanz-Serna, & Stuart, 2013; Roberts, Gelman, & Gilks, 1997). Em situações dimensionais mais baixas, o poder computacional aumentado pode compensar a eficiência mais baixa até certo ponto. Mas em situações de modelagem de dimensões mais altas e mais complexas, computadores maiores e mais rápidos sozinhos raramente são suficientes para superar o desafio.

Metropolis – Implementação

No nosso exemplo didático vamos partir do pressuposto que \(J_t(\boldsymbol{\theta}^{(*)} \mid \boldsymbol{\theta}^{(t-1)})\) é simétrico à \(J_t \left(\boldsymbol{\theta}^{(*)} \mid \boldsymbol{\theta}^{(t-1)} \right) = J_t \left(\boldsymbol{\theta}^{(t-1)} \mid \boldsymbol{\theta}^{(*)} \right)\), portanto vamos apenas demonstrar o algoritmo de Metropolis (e não o algoritmo de Metropolis-Hastings).

O Stan (Carpenter et al., 2017) (e consequentemente seu ecossistema inteiro de pacotes) não tem implementações de outros algoritmos a não ser o HMC (Hamiltonean Monte Carlo), portanto abaixo criei um amostrador Metropolis para o nosso exemplo didático. No fim ele imprime a porcentagem total de aceitação das propostas. Aqui estamos usando a mesma distribuição de propostas para tanto \(X\) e \(Y\): uma distribuição uniforme parameterizada com um parâmetro largura width:

\[ X \sim \text{Uniforme} \left( X - \frac{\text{largura}}{2}, X + \frac{\text{largura}}{2} \right) \\ Y \sim \text{Uniforme} \left( Y - \frac{\text{largura}}{2}, Y + \frac{\text{largura}}{2} \right) \] O pacote mnormt possui algumas funcionalidades para lidar com distribuições multivariadas, a função dmnorm() em especial calcula a função densidade de probabilidade (FDP)⁴ de uma distribuição normal multivariada, que é usada no cálculo proporção das probabilidades \(r\):

\[ \begin{aligned} r &= \frac{ \operatorname{FDP}\left( \text{Normal Multivariada} \left( \begin{bmatrix} x_{\text{proposto}} \\ y_{\text{proposto}} \end{bmatrix} \right) \Bigg| \text{Normal Multivariada} \left( \begin{bmatrix} \mu_X \\ \mu_Y \end{bmatrix}, \mathbf{\Sigma} \right) \right)} { \operatorname{FDP}\left( \text{Normal Multivariada} \left( \begin{bmatrix} x_{\text{atual}} \\ y_{\text{atual}} \end{bmatrix} \right) \Bigg| \text{Normal Multivariada} \left( \begin{bmatrix} \mu_X \\ \mu_Y \end{bmatrix}, \mathbf{\Sigma} \right) \right)}\\ &=\frac{\operatorname{FDP}_{\text{proposto}}}{\operatorname{FDP}_{\text{atual}}}\\ &= \exp\Big( \log\left(\operatorname{FDP}_{\text{proposto}}\right) - \log\left(\operatorname{FDP}_{\text{atual}}\right) \Big) \end{aligned} \]

metropolis <- function(S, half_width,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho,
                       start_x, start_y,
                       seed = 123) {
   set.seed(seed)
   Sigma <- diag(2)
   Sigma[1, 2] <- rho
   Sigma[2, 1] <- rho
   draws <- matrix(nrow = S, ncol = 2)
   x <- start_x
   y <- start_y
   accepted <- 0
   draws[1, 1] <- x
   draws[1, 2] <- y
   for (s in 2:S) {
      x_ <- runif(1, x - half_width, x + half_width)
      y_ <- runif(1, y - half_width, y + half_width)
      r <- exp(mnormt::dmnorm(c(x_, y_), mean = c(mu_X, mu_Y), varcov = Sigma, log = TRUE) -
                        mnormt::dmnorm(c(x, y), mean = c(mu_X, mu_Y), varcov = Sigma, log = TRUE))
      if (r > runif(1, 0, 1)) {
        x <- x_
        y <- y_
        accepted <- accepted + 1
      }
      draws[s, 1] <- x
      draws[s, 2] <- y
   }
   print(paste0("Taxa de aceitação ", accepted / S))
   return(draws)
}

n_sim <- 1e4

Vamos executar nosso algoritmo Metropolis com 10,000 iterações.

X_met <- metropolis(
  S = n_sim, half_width = 2.75,
  mu_X = 0, mu_Y = 0,
  sigma_X = 1, sigma_Y = 1,
  rho = r,
  start_x = -2.5, start_y = 2.5
)

[1] "Taxa de aceitação 0.2076"

head(X_met, 7)

      [,1] [,2]
[1,] -2.50  2.5
[2,] -2.50  2.5
[3,] -2.50  2.5
[4,] -2.50  2.5
[5,] -2.50  2.5
[6,] -1.52  2.9
[7,]  0.68  1.5

Na nossa primeira execução do algoritmo Metropolis temos como resultado uma matriz X_met com 10,000 linhas e 2 colunas (uma para cada valor de \(X\) e \(Y\), que passarei a chamar de \(\theta_1\) e \(\theta_2\), respectivamente). Vejam que a aceitação das propostas ficou em 20.8%, o esperado para algoritmos Metropolis (em torno de 20-25%) (Beskos et al., 2013; Roberts et al., 1997).

Para métricas de convergência e desempenho vamos usar a função rstan::monitor() que simula um print(stanfit)⁵mas para matrizes.

res <- monitor(X_met, digits_summary = 1)

Inference for the input samples (2 chains: each with iter = 10000; warmup = 5000):

     Q5 Q50 Q95 Mean SD  Rhat Bulk_ESS Tail_ESS
V1 -1.6   0 1.7    0  1     1      952      909

For each parameter, Bulk_ESS and Tail_ESS are crude measures of 
effective sample size for bulk and tail quantities respectively (an ESS > 100 
per chain is considered good), and Rhat is the potential scale reduction 
factor on rank normalized split chains (at convergence, Rhat <= 1.05).

neff <- res[, "n_eff"]
reff <- mean(neff / (nrow(X_met))) #  9.5%

Vejam que o número de amostras eficientes em relação ao número total de iterações reff é 9,5% para todas as iterações incluindo warm-up.

Metropolis – Intuição Visual

Eu acredito que uma boa intuição visual, mesmo que você não tenha entendido nenhuma fórmula matemática, é a chave para você começar a jornada de aprendizagem. Portanto fiz algumas animações com GIFs.

A animação na figura 6 mostra as 100 primeiras simulações do algoritmo Metropolis usado para gerar X_met. Vejam que em diversas iterações a proposta é recusada e o algoritmo amostra os parâmetros \(\theta_1\) e \(\theta_2\) do estado anterior (que se torna o atual, pois a proposta é recusada).

Observação: HPD é a sigla para Highest Probability Density (que é o intervalo de 90% de probabilidade da posterior).

df100 <- data.frame(
    id = rep(1, 100),
    iter = 1:100,
    th1 = X_met[1:100, 1],
    th2 = X_met[1:100, 2],
    th1l = c(X_met[1, 1], X_met[1:(100 - 1), 1]),
    th2l = c(X_met[1, 2], X_met[1:(100 - 1), 2])
)

labs1 <- c("Amostras", "Iterações do Algoritmo", "90% HPD")

p1 <- ggplot() +
  geom_jitter(data = df100, width = 0.05, height = 0.05,
             aes(th1, th2, group = id, color = "1"), alpha = 0.3) +
  geom_segment(data = df100, aes(x = th1, xend = th1l, color = "2",
                                 y = th2, yend = th2l)) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "3"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Metropolis", subtitle = "100 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("red", "forestgreen", "blue"), labels = labs1) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA, NA), linetype = c(0, 1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

animate(p1 +
  transition_reveal(along = iter) +
  shadow_trail(0.01),
  # animation options
  height = 7, width = 7, units = "in", res = 300
)

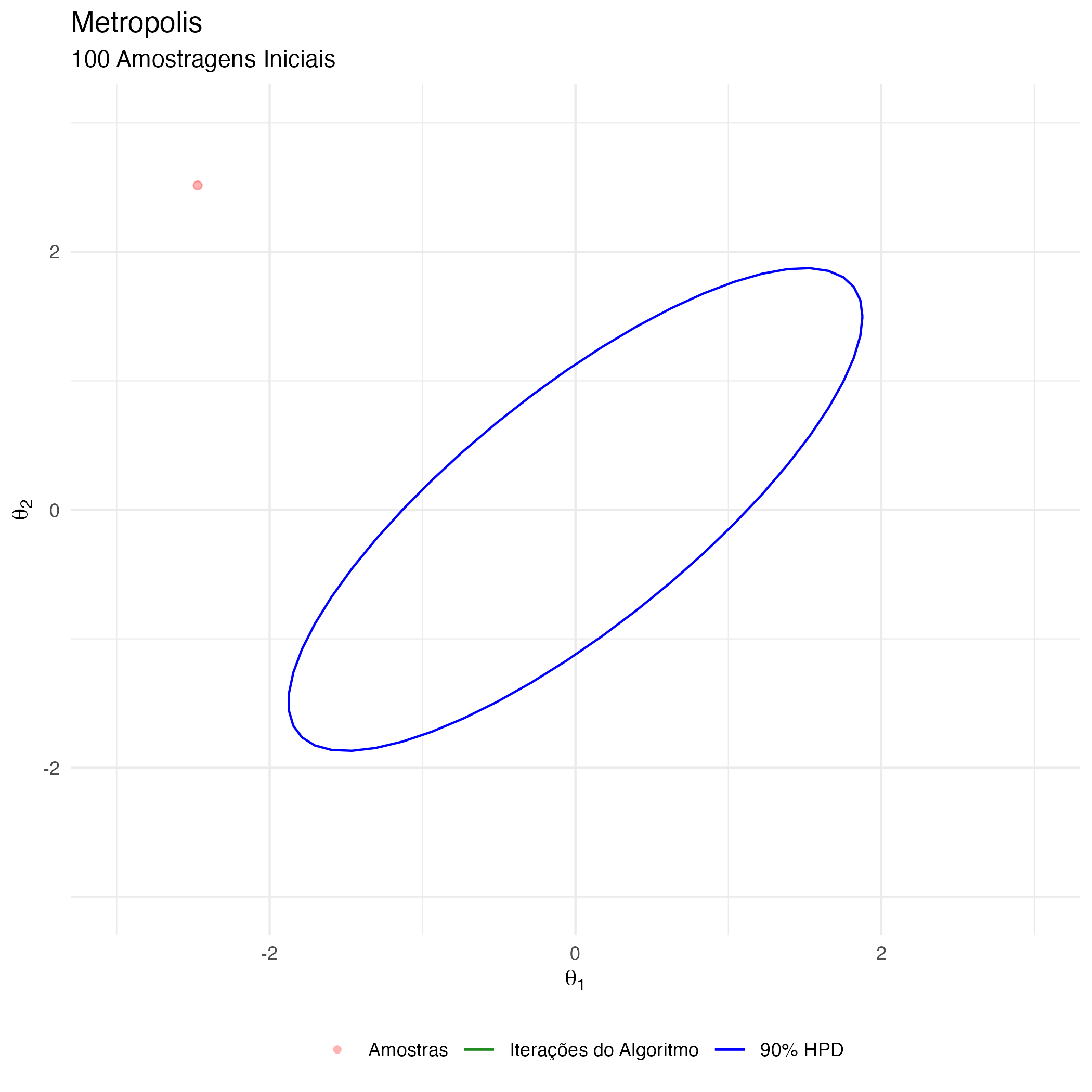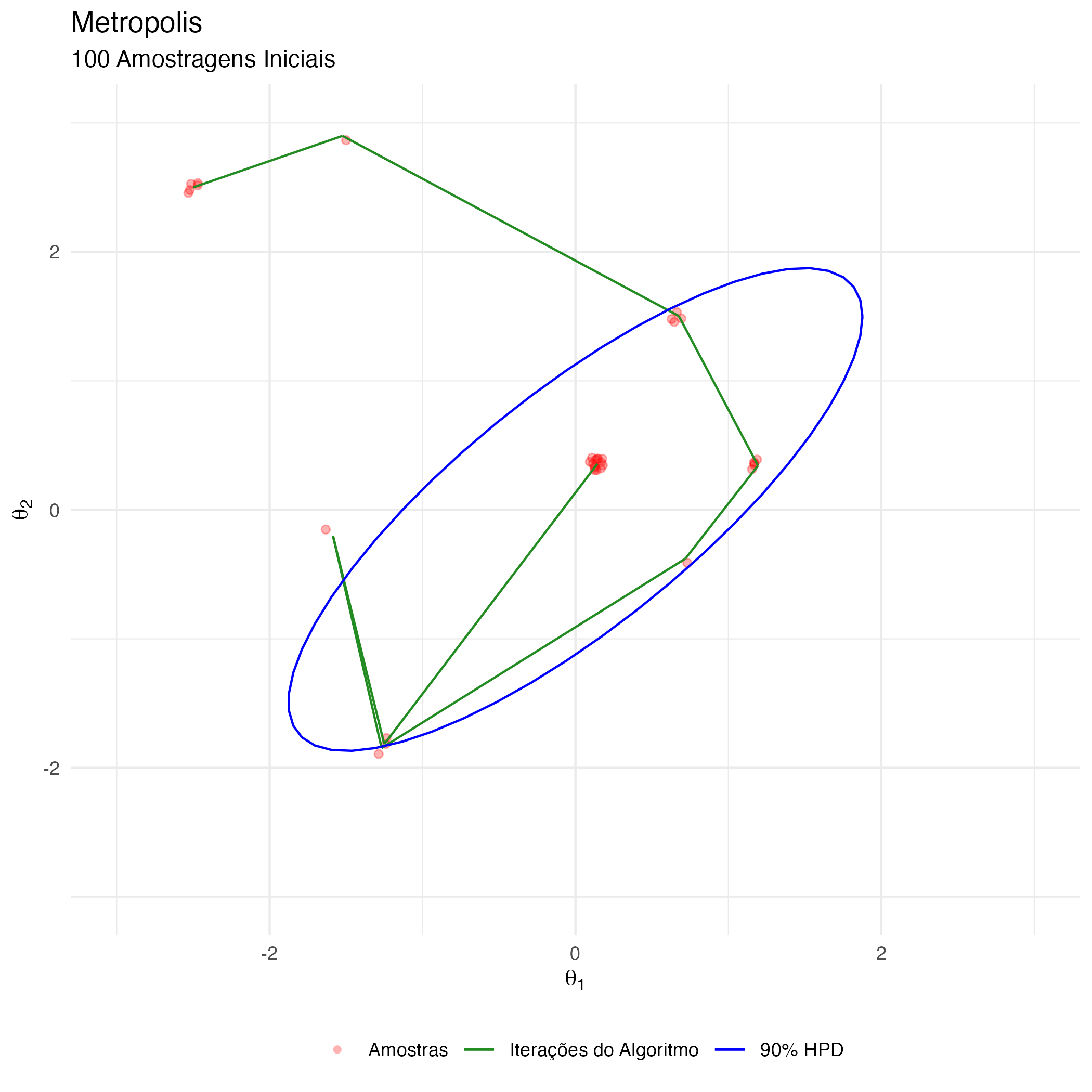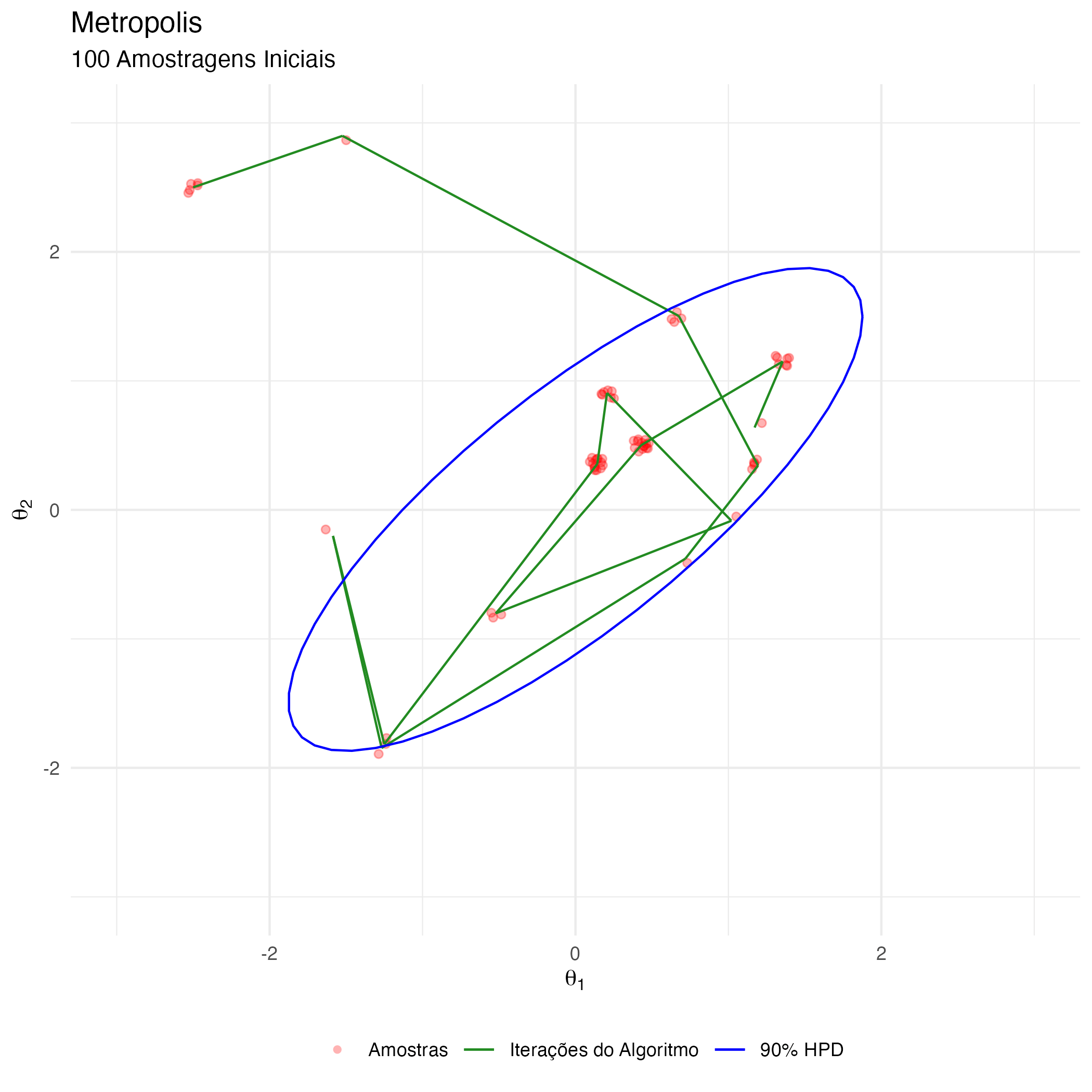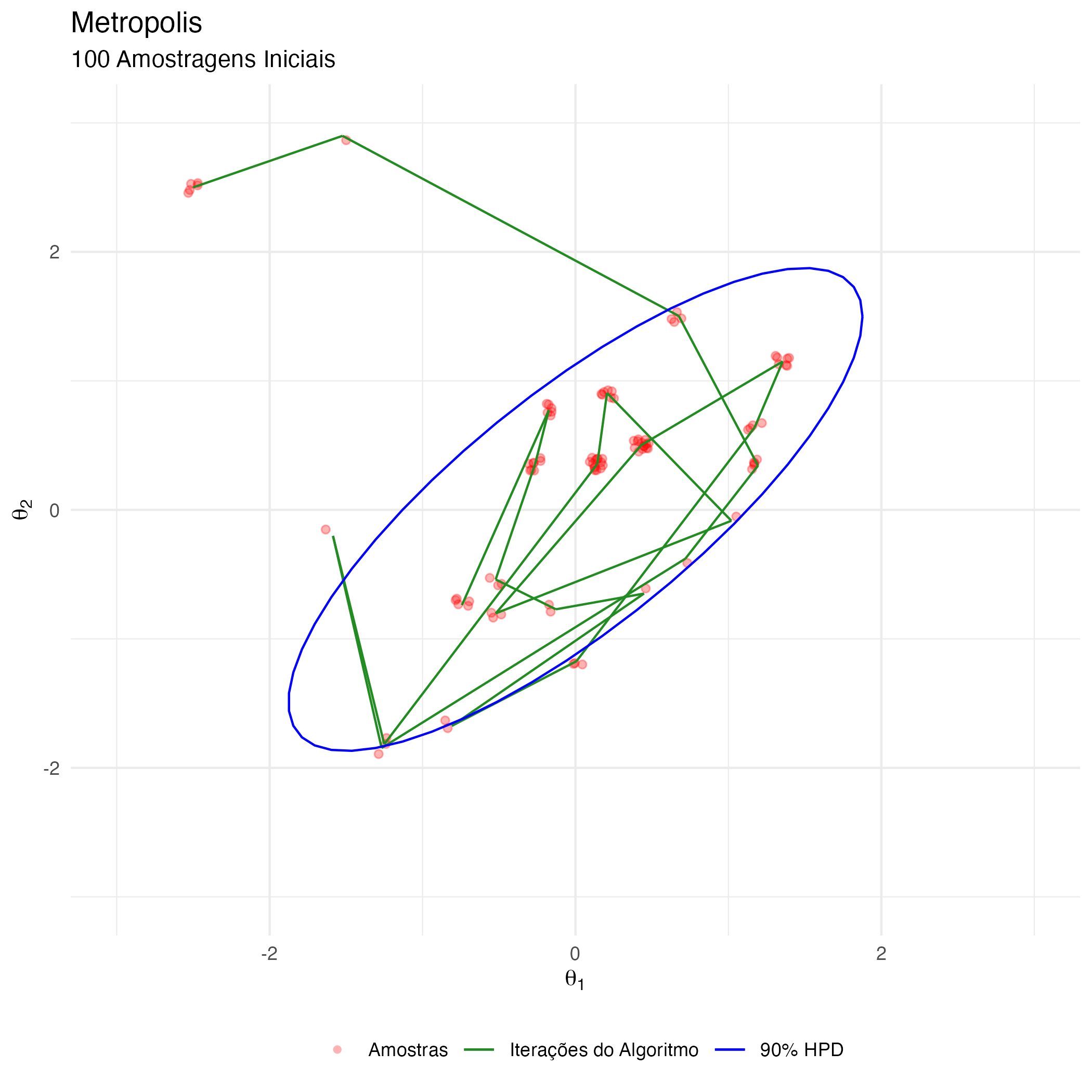
Figure 6: Animação Metropolis

Na figura 7 é possível ver como ficaram as primeiras 1.000 simulações excluindo 1.000 iterações iniciais como warmup.

# Take all the 10,000 observations after warmup of 1,000
warm <- 1e3
dfs <- data.frame(
  th1 = X_met[(warm + 1):nrow(X_met), 1],
  th2 = X_met[(warm + 1):nrow(X_met), 2]
)

labs2 <- c("Amostras", "90% HPD")

ggplot() +
  geom_point(data = dfs[1:1000, ],
             aes(th1, th2, color = "1"), alpha = 0.3) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "2"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Metropolis", subtitle = "1.000 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("steelblue", "blue"), labels = labs2) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA), linetype = c(0, 1), alpha = c(1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

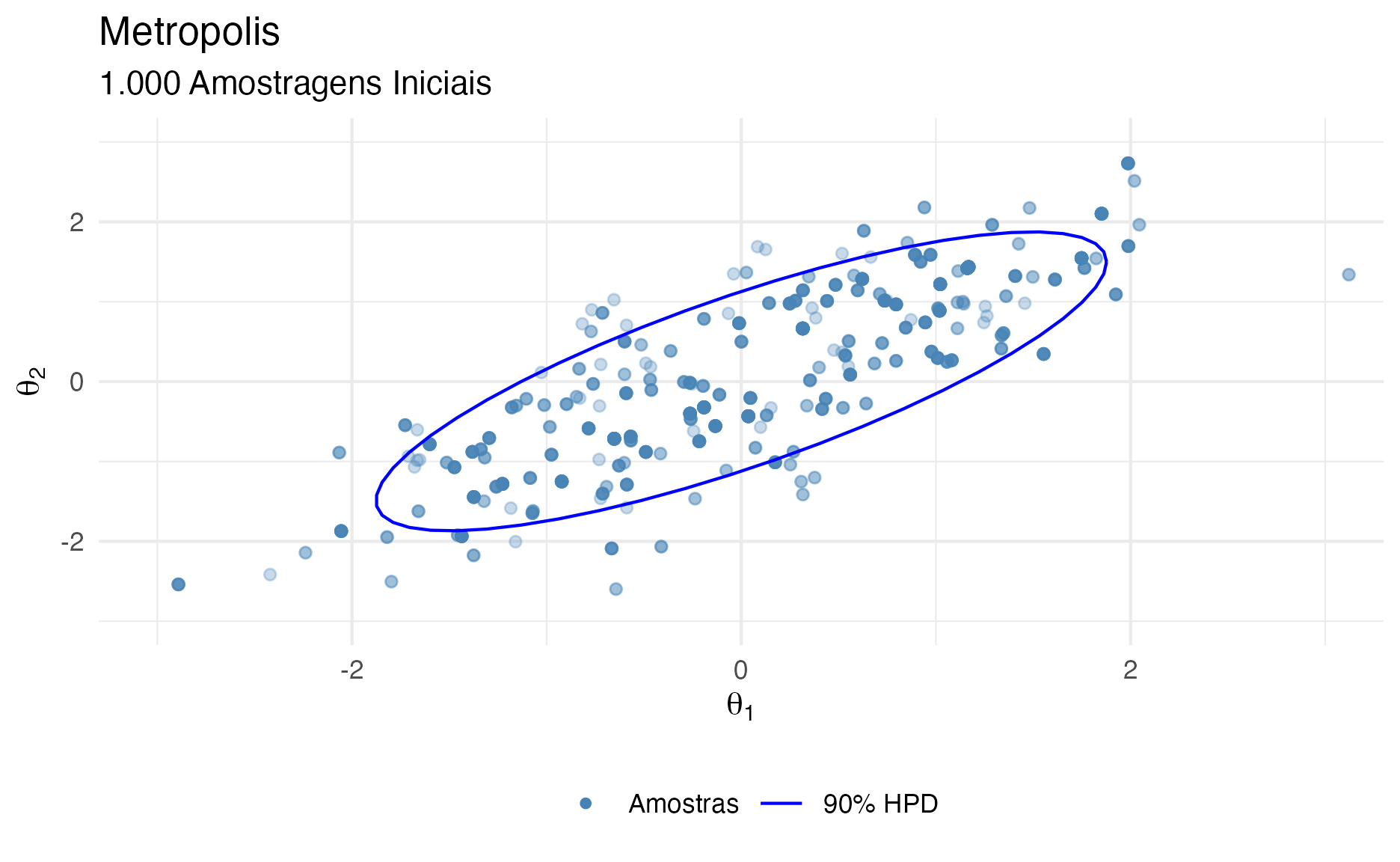
Figure 7: Primeiras 1.000 simulações Metropolis após descarte de 1.000 iterações como warmup

E na figura 8 é possível ver as restantes 9.000 simulações excluindo 1.000 iterações iniciais como warmup.

# Show all 10,000 samples
ggplot() +
  geom_point(data = dfs,
             aes(th1, th2, color = "1"), alpha = 0.3) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "2"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Metropolis", subtitle = "10.000 Amostragens",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("steelblue", "blue"), labels = labs2) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA), linetype = c(0, 1), alpha = c(1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

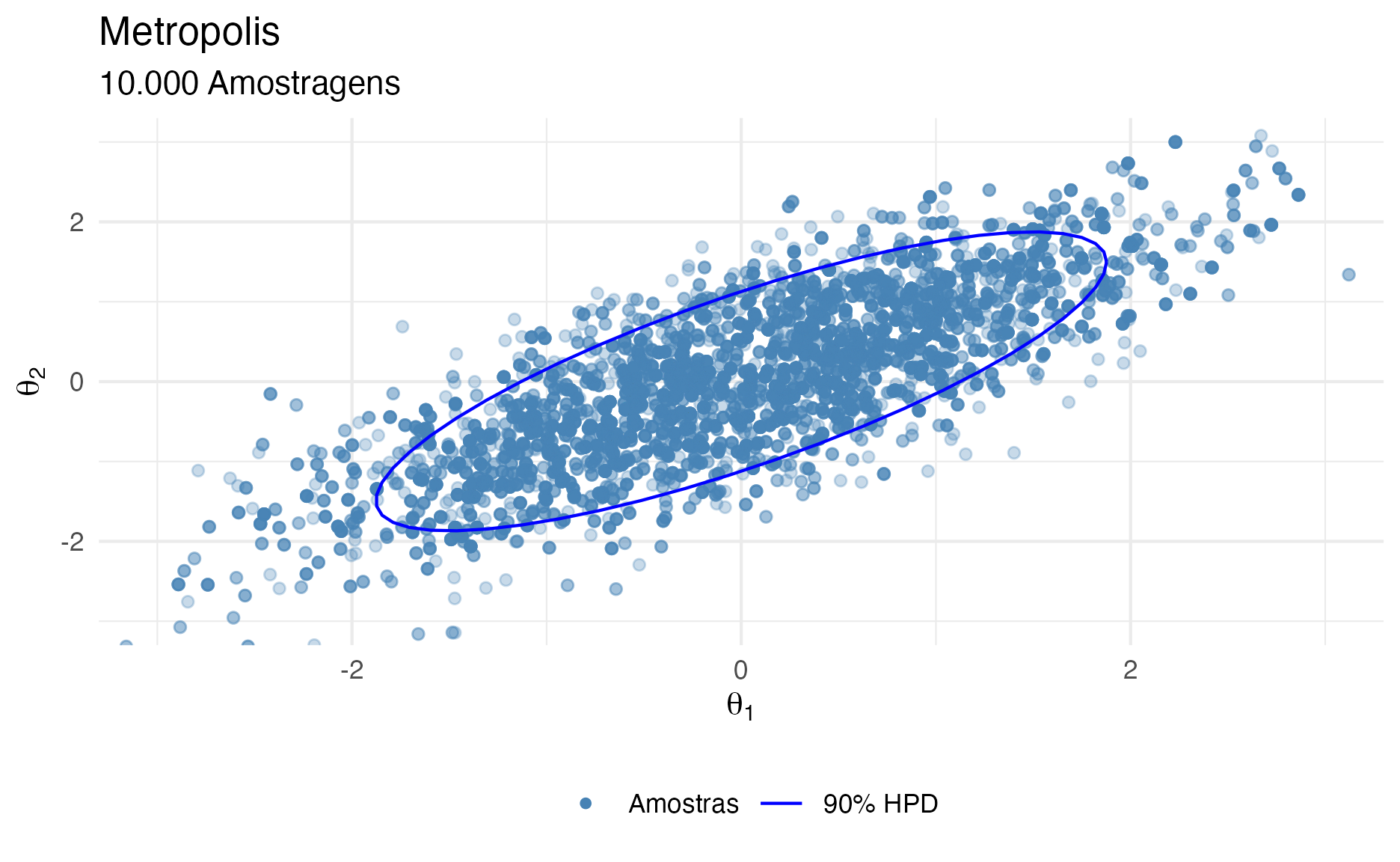
Figure 8: 9.000 simulações Metropolis após descarte de 1.000 iterações como warmup

Gibbs

Para contornar o problema de baixa taxa de aceitação do algoritmo de Metropolis (e Metropolis-Hastings) foi desenvolvido o algoritmo de Gibbs que não possui uma regra de aceitação/rejeição para a mudança de estado da corrente Markov. Todas as propostas são aceitas.

O algoritmo de Gibbs teve ideia original concebida pelo físico Josiah Willard Gibbs (figura 9), em referência a uma analogia entre um algoritmo de amostragem e a física estatística (statistical physics um ramo da física que tem sua base em mecânica estatística statistical mechanics). O algoritmo foi descrito pelos irmãos Stuart e Donald Geman (figura 9) em 1984 (Geman & Geman, 1984), cerca de oito décadas após a morte de Gibbs.

Figure 9: Da esquerda para direita: Josiah Gibbs,Stuart Geman e Donald Geman – Figuras de https://www.wikipedia.org

O algoritmo de Gibbs é muito útil em espaços amostrais multidimensionais (no qual há bem mais que 2 parâmetros a serem amostrados da probabilidade posterior). Também é conhecido como amostragem condicional alternativa (alternating conditional sampling), pois amostramos sempre um parâmetro condicionado à probabilidade dos outros parâmetros do modelo.

O algoritmo de Gibbs pode ser visto como um caso especial do algoritmo de Metropolis-Hastings porque todas as propostas são aceitas (Gelman, 1992).

Algoritmo de Gibbs

A essência do algoritmo de Gibbs é a amostragem de parâmetros condicionada à outros parâmetros \(P(\theta_1 \mid \theta_2, \dots \theta_p)\).

O algoritmo de Gibbs pode ser descrito na seguinte maneira⁶ (\(\boldsymbol{\theta}\) é o parâmetro, ou conjunto de parâmetros, de interesse e \(y\) são os dados):

1. Defina \(P(\theta_1), P(\theta_2), \dots, P(\theta_p)\): a probabilidade prévia (prior) de cada um dos parâmetros \(\boldsymbol{\theta}\).

2. Defina um ponto inicial \(\boldsymbol{\theta}^{(0)} \in \mathbb{R}^p\) do qual \(P\left(\boldsymbol{\theta}^{(0)} \mid y \right) > 0\) Geralmente amostramos de uma distribuição normal ou de uma distribuição especificada como a distribuição prévia (prior) de \(\boldsymbol{\theta}\).

3. Para \(t = 1,2,\dots\): Designe: \[\boldsymbol{\theta}^{(t)} = \begin{cases} \theta^{(t)}_1 &\sim P \left(\theta_1 \mid \theta^{(0)}_2, \dots, \theta^{(0)}_p \right) \\ \theta^{(t)}_2 &\sim P \left(\theta_2 \mid \theta^{(t-1)}_1, \dots, \theta^{(0)}_p \right) \\ &\vdots \\ \theta^{(t)}_p &\sim P \left(\theta_p \mid \theta^{(t-1)}_1, \dots, \theta^{(t-1)}_{p-1} \right) \end{cases}\]

Limitações do Algoritmo de Gibbs

A principal limitação do algoritmo de Gibbs é com relação a amostragem condicional alternativa.

Se compararmos com o algoritmo Metropolis (e consequentemente Metropolis-Hastings) temos propostas aleatórias de uma distribuição de propostas na qual amostramos cada parâmetro incondicionalmente à outros parâmetros. Para que as propostas nos levem a locais corretos da probabilidade posterior para amostrarmos temos uma regra de aceitação/rejeição dessas propostas, se não as amostras do algoritmo de Metropolis não se aproximariam à distribuição-alvo de interesse. As mudanças de estado da corrente Markov são então executadas multidimensionalmente⁷. Como você viu nas figuras 6, 7 e 8 de intuição visual do algoritmo de Metropolis, em um espaço 2-D (como é o nosso exemplo didático bivariado normal), quando há uma mudança de estado na corrente Markov, o novo local de proposta considera tanto \(\theta_1\) quanto \(\theta_2\), provocando uma movimentação na diagonal no espaço amostral 2-D.

No caso do algoritmo de Gibbs, no nosso exemplo, essa movimentação se dá apenas em um único parâmetro, pois amostramos sequencialmente e condicionalmente à outros parâmetros. Isto provoca movimentos horizontais (no caso de \(\theta_1\)) e movimentos verticais (no caso de \(\theta_2\)), mas nunca movimentos diagonais como o que vemos no algoritmo de Metropolis.

Gibbs – Implementação

O Stan (Carpenter et al., 2017) (e consequentemente seu ecossistema inteiro de pacotes) não tem implementações de outros algoritmos a não ser o HMC (Hamiltonian Monte Carlo), portanto abaixo criei um amostrador Gibbs para o nosso exemplo didático.

Aqui temos algumas coisas novas comparando com a implementação do amostrador Metropolis. Primeiro para amostrar condicionalmente os parâmetros \(P(\theta_1 \mid \theta_2)\) e \(P(\theta_2 \mid \theta_1)\), precisamos criar duas variáveis novas beta (\(\beta\)) e lambda (\(\lambda\)). Essas variáveis representam a correlação entre \(X\) e \(Y\) (\(\theta_1\) e \(\theta_2\) respectivamente). E então usamos essas variáveis na amostragem de \(\theta_1\) e \(\theta_2\):

\[ \begin{aligned} \beta &= \rho \cdot \frac{\sigma_Y}{\sigma_X} = \rho \\ \lambda &= \rho \cdot \frac{\sigma_X}{\sigma_Y} = \rho \\ \sigma_{YX} &= 1 - \rho^2\\ \sigma_{XY} &= 1 - \rho^2\\ \theta_1 &\sim \text{Normal} \bigg( \mu_X + \lambda \cdot (y^* - \mu_Y), \sigma_{XY} \bigg) \\ \theta_2 &\sim \text{Normal} \bigg( \mu_y + \beta \cdot (x^* - \mu_X), \sigma_{YX} \bigg). \end{aligned} \]

gibbs <- function(S,
                  mu_X = 0, mu_Y = 0,
                  sigma_X = 1, sigma_Y = 1,
                  rho,
                  start_x, start_y,
                  seed = 123) {
   set.seed(seed)
   Sigma <- diag(2)
   Sigma[1, 2] <- rho
   Sigma[2, 1] <- rho
   draws <- matrix(nrow = S, ncol = 2)
   x <- start_x
   y <- start_y
   beta <- rho * sigma_Y / sigma_X
   lambda <- rho * sigma_X / sigma_Y
   sqrt1mrho2 <- sqrt(1 - rho^2)
   sigma_YX <- sigma_Y * sqrt1mrho2
   sigma_XY <- sigma_X * sqrt1mrho2
   draws[1, 1] <- x
   draws[1, 2] <- y
   for (s in 2:S) {
     if (s %% 2 == 0) {
        y <- rnorm(1, mu_Y + beta * (x - mu_X), sigma_YX)
     }
     else {
        x <- rnorm(1, mu_X + lambda * (y - mu_Y), sigma_XY)
     }
     draws[s, 1] <- x
     draws[s, 2] <- y
   }
   return(draws)
}

Vamos executar nosso algoritmo Gibbs com 10,000 iterações.

X_gibbs <- gibbs(
  S = n_sim,
  mu_X = 0, mu_Y = 0,
  sigma_X = 1, sigma_Y = 1,
  rho = r,
  start_x = -2.5, start_y = 2.5
)
head(X_gibbs, 7)

      [,1]  [,2]
[1,] -2.50  2.50
[2,] -2.50 -2.34
[3,] -2.01 -2.34
[4,] -2.01 -0.67
[5,] -0.49 -0.67
[6,] -0.49 -0.32
[7,]  0.77 -0.32

Na nossa primeira execução do algoritmo Gibbs temos como resultado uma matriz X_gibbs com 10,000 linhas e 2 colunas (as mesmas condições já mostradas no exemplo anterior com algoritmo Metropolis).

res <- monitor(X_gibbs, digits_summary = 1)

Inference for the input samples (2 chains: each with iter = 10000; warmup = 5000):

     Q5 Q50 Q95 Mean SD  Rhat Bulk_ESS Tail_ESS
V1 -1.7   0 1.6    0  1     1     1156     1972

For each parameter, Bulk_ESS and Tail_ESS are crude measures of 
effective sample size for bulk and tail quantities respectively (an ESS > 100 
per chain is considered good), and Rhat is the potential scale reduction 
factor on rank normalized split chains (at convergence, Rhat <= 1.05).

neff <- res[, "n_eff"]
reff <- mean(neff / (nrow(X_gibbs) / 2)) #  23.2%

Vejam que o número de amostras eficientes em relação ao número total de iterações reff⁸ é 23% para todas as iterações incluindo warm-up. A eficiência do algoritmo Gibbs, no nosso exemplo didático, é o mais que dobro da eficiência do algoritmo de Metropolis (9,5% vs 23%).

Gibbs – Intuição Visual

A animação na figura 10 mostra as 100 primeiras simulações do algoritmo Gibbs usado para gerar X_gibbs. Vejam que aqui não há movimentação na diagonal no espaço amostral devido à amostragem condicional alternativa dos parâmetros \(\theta_1\) e \(\theta_2\). A movimentação do algoritmo Gibbs no espaço amostral está condicionada a apenas um movimento por dimensão de parâmetro (que no nosso exemplo didático 2-D são as dimensões horizontais \(\theta_1\) e verticais \(\theta_2\)).

df100 <- data.frame(
    id = rep(1, 100),
    iter = 1:100,
    th1 = X_gibbs[1:100, 1],
    th2 = X_gibbs[1:100, 2],
    th1l = c(X_gibbs[1, 1], X_gibbs[1:(100 - 1), 1]),
    th2l = c(X_gibbs[1, 2], X_gibbs[1:(100 - 1), 2])
)

labs1 <- c("Amostras", "Iterações do Algoritmo", "90% HPD")

ind1 <- (1:50) * 2 - 1
df100s <- df100
df100s[ind1 + 1, 3:4] <- df100s[ind1, 3:4]
p1 <- ggplot() +
  geom_point(data = df100s,
             aes(th1, th2, group = id, color = "1")) +
  geom_segment(data = df100, aes(x = th1, xend = th1l, color = "2",
                                 y = th2, yend = th2l)) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "3"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Gibbs", subtitle = "100 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("red", "forestgreen", "blue"), labels = labs1) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA, NA), linetype = c(0, 1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

animate(p1 +
  transition_reveal(along = iter) +
  shadow_trail(0.01),
  # animation options
  height = 7, width = 7, units = "in", res = 300
)

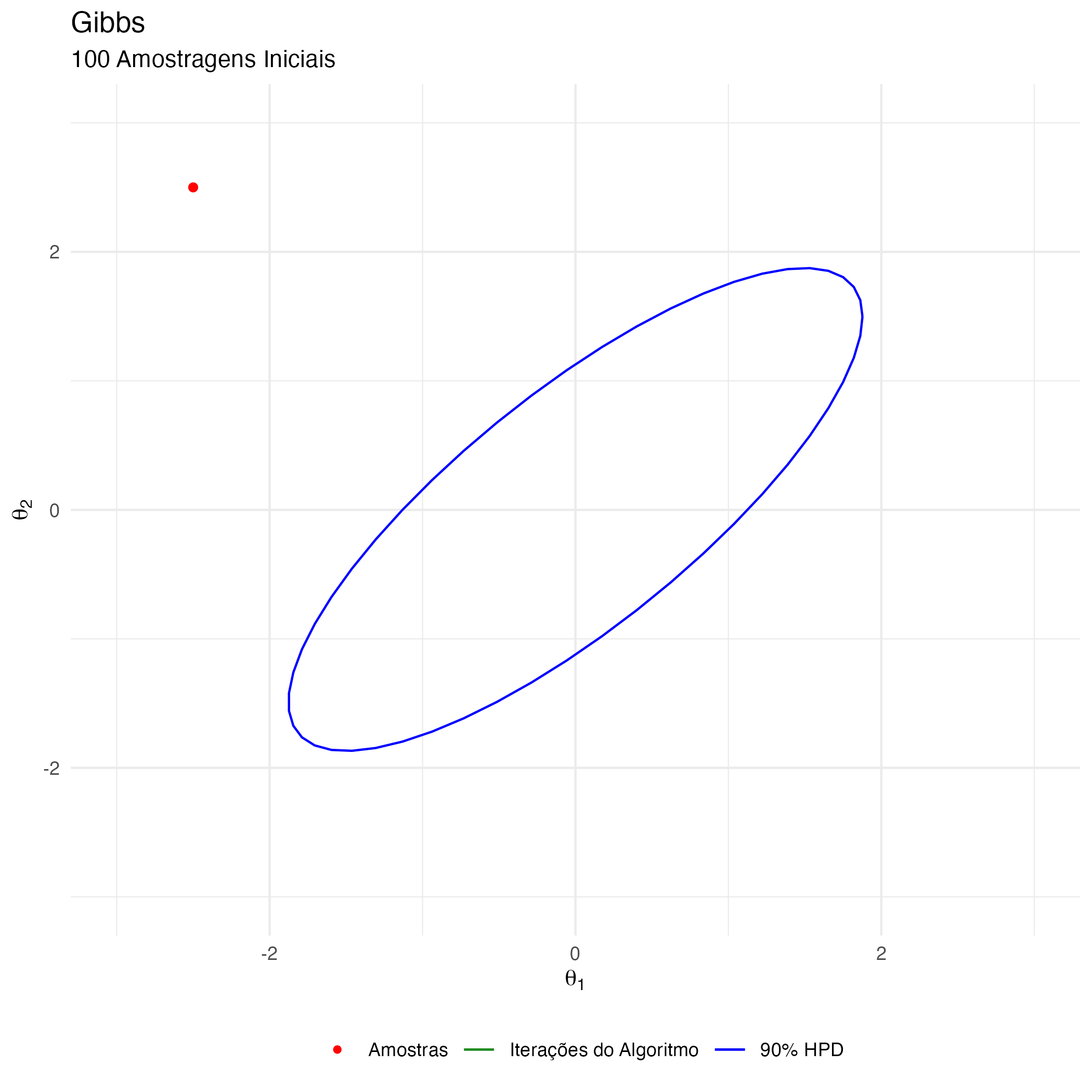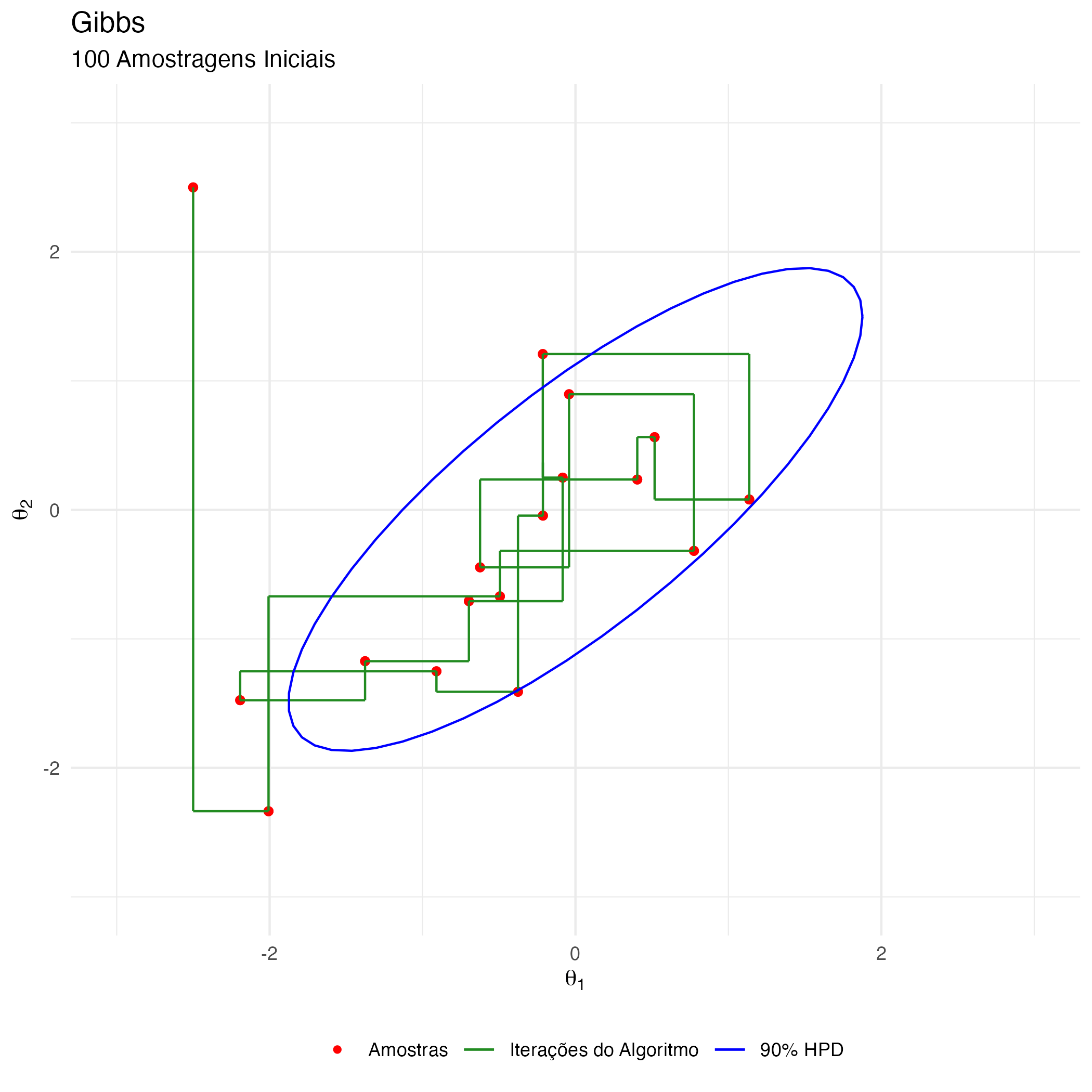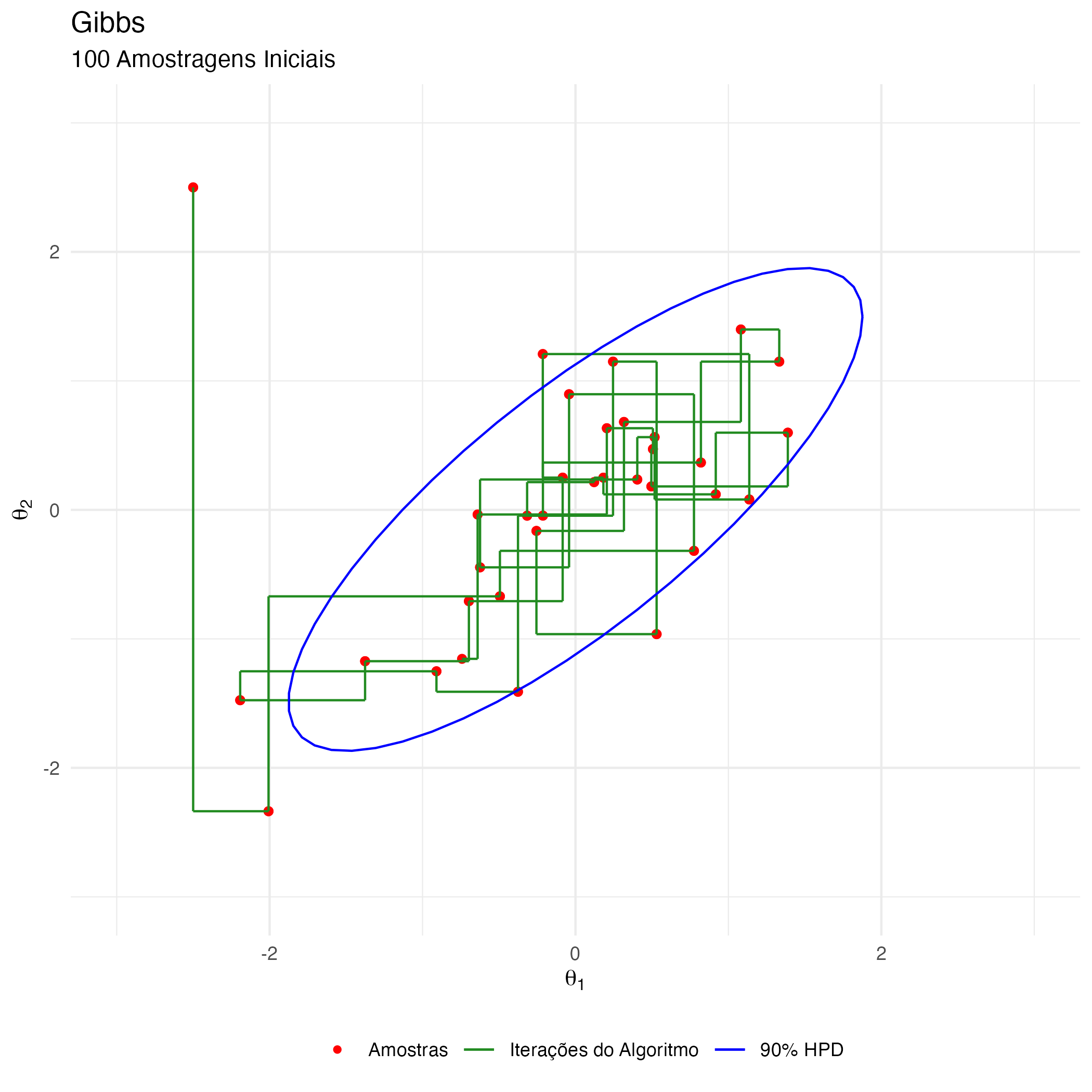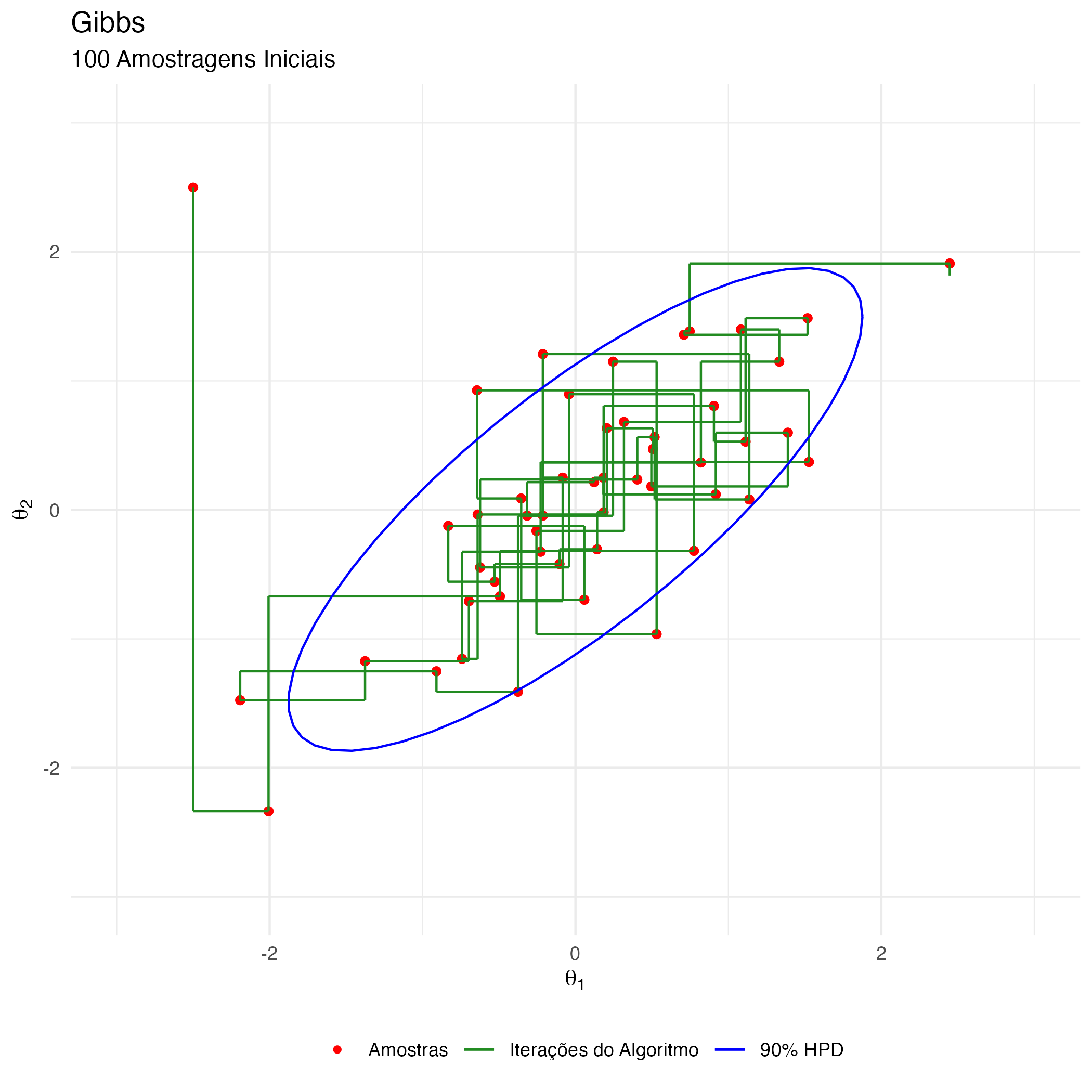
Figure 10: Animação Gibbs

Na figura 11 é possível ver como ficaram as primeiras 1.000 simulações excluindo 1.000 iterações iniciais como warmup.

# Take all the 10,000 observations after warmup of 1,000
warm <- 1e3
dfs <- data.frame(
  th1 = X_gibbs[(warm + 1):nrow(X_gibbs), 1],
  th2 = X_gibbs[(warm + 1):nrow(X_gibbs), 2]
)

labs2 <- c("Amostras", "90% HPD")

ggplot() +
  geom_point(data = dfs[1:1000, ],
             aes(th1, th2, color = "1"), alpha = 0.3) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "2"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Gibbs", subtitle = "1.000 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("steelblue", "blue"), labels = labs2) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA), linetype = c(0, 1), alpha = c(1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

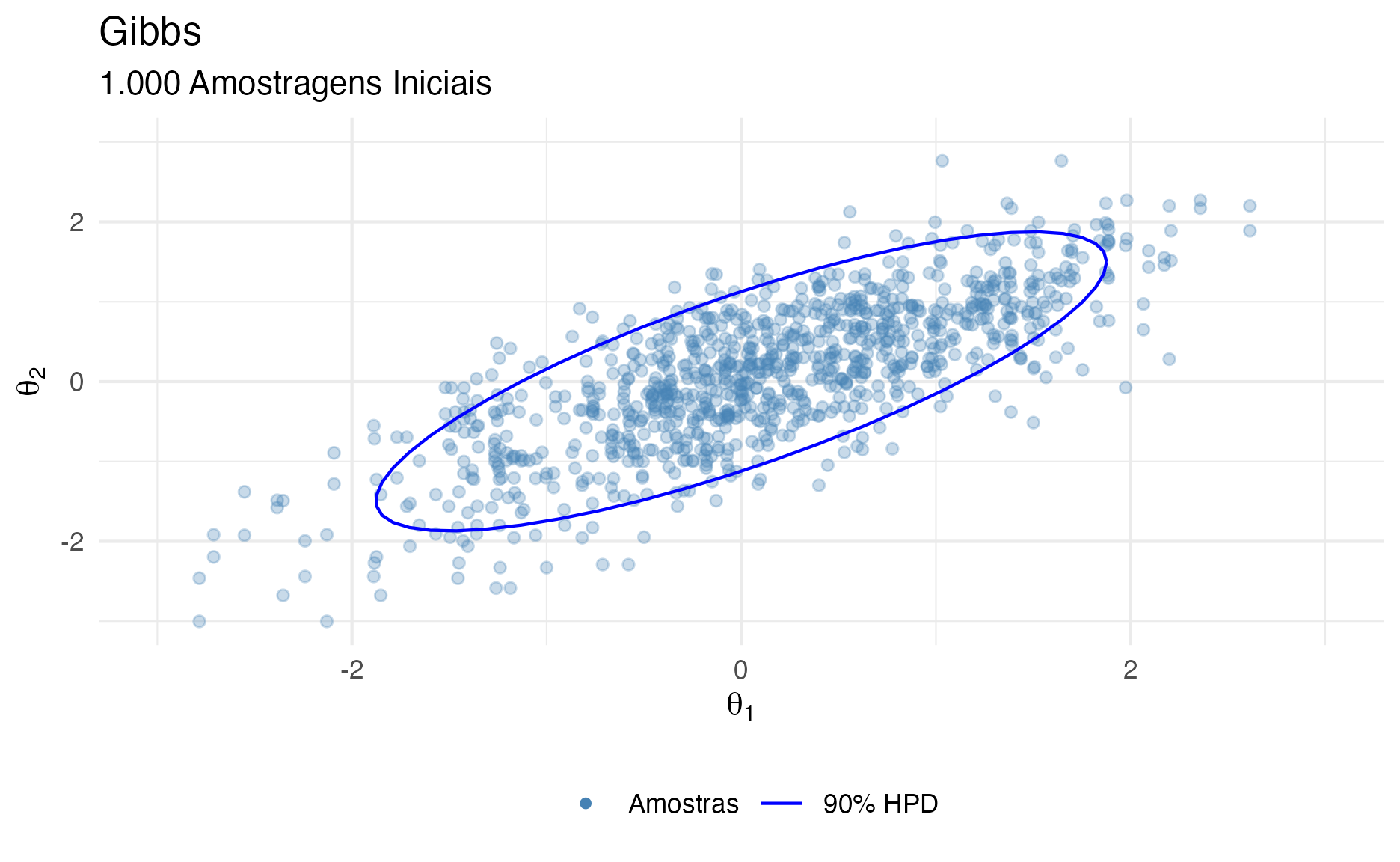
Figure 11: Primeiras 1.000 simulações Gibbs após descarte de 1.000 iterações como warmup

E na figura 12 é possível ver as restantes 9.000 simulações excluindo 1.000 iterações iniciais como warmup.

# Show all 10,000 samples
ggplot() +
  geom_point(data = dfs,
             aes(th1, th2, color = "1"), alpha = 0.3) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "2"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Gibbs", subtitle = "10.000 Amostragens",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("steelblue", "blue"), labels = labs2) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA), linetype = c(0, 1), alpha = c(1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

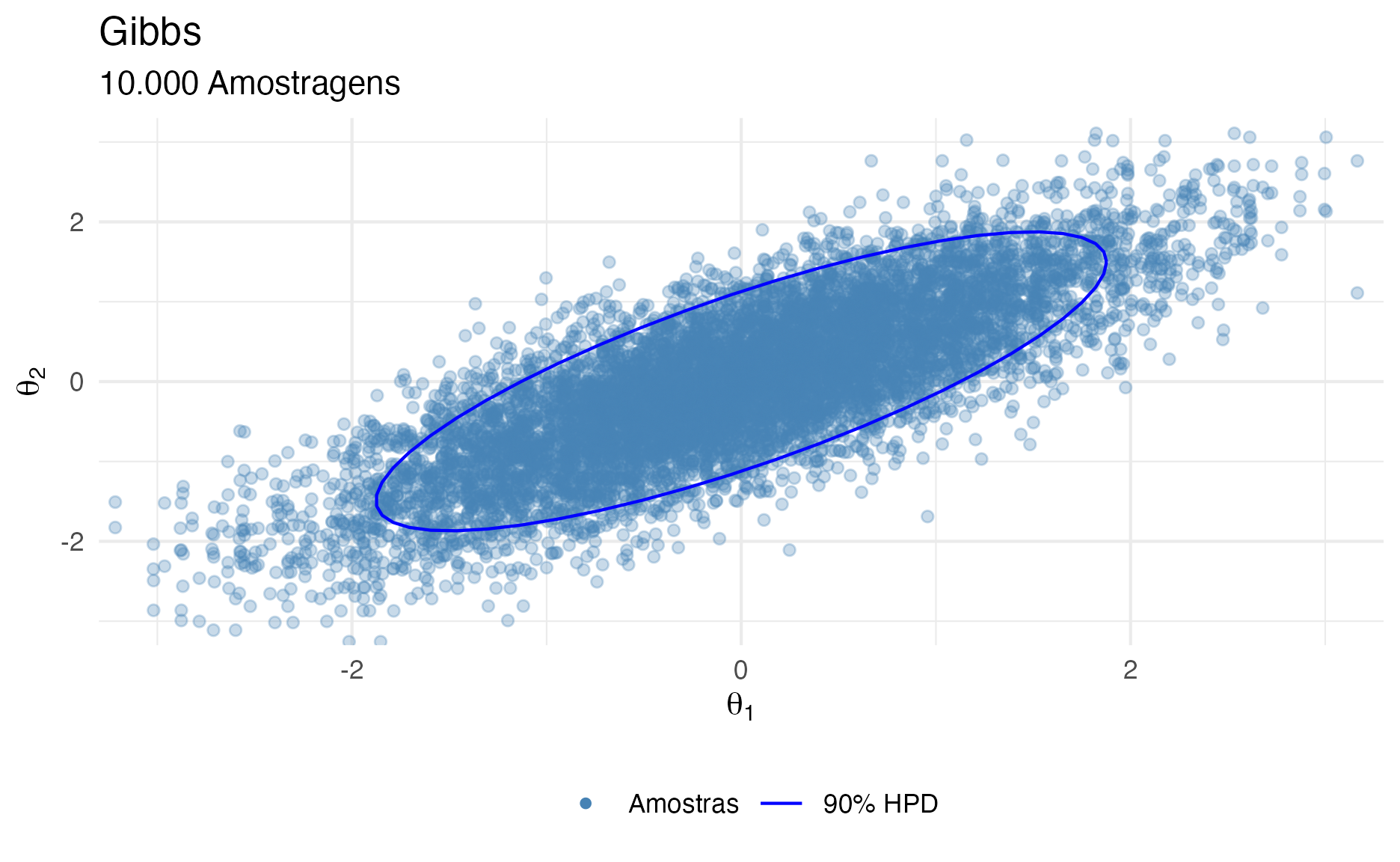
Figure 12: 9.000 simulações Gibbs após descarte de 1.000 iterações como warmup

O que acontece quando rodamos correntes Markov em paralelo?

Como as correntes Markov são independentes, podemos executá-las em paralelo no computador. A chave para isso é definir pontos iniciais diferentes de cada corrente Markov (caso você use como ponto inicial uma amostra de uma distribuição prévia dos parâmetros isto não é um problema). Vamos usar o mesmo exemplo didático de uma distribuição normal bivariada \(X\) e \(Y\) que usamos nos exemplos anteriores, mas agora com 4 correntes Markov com diferentes pontos de início.

starts <- list(c(-2.5, 2.5),
               c(2.5, -2.5),
               c(-2.5, -2.5),
               c(2.5, 2.5)
               )

Correntes Markov em Paralelo – Metropolis

Para criar 4 correntes Markov com pontos diferentes de início dos parâmetros, usamos 4 vezes o amostrador Metropolis que codificamos anterior, mas agora passamos diferentes argumentos start_x e start_y, além de diferentes seed do pseudogerador de número aleatórios para termos diferentes comportamentos das correntes Markov. Todo o resultado é combinado em um dataframe com uma coluna id representando o número de cada corrente (de 1 a 4).

library(dplyr)
n_sim <- 100
Xs_met <- bind_rows(
  as_tibble(metropolis(S = n_sim, half_width = 2.75,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = -2.5, start_y = 2.5,
                       seed = 1)),
  as_tibble(metropolis(S = n_sim, half_width = 2.75,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = 2.5, start_y = -2.5,
                       seed = 2)),
  as_tibble(metropolis(S = n_sim, half_width = 2.75,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = -2.5, start_y = -2.5,
                       seed = 3)),
  as_tibble(metropolis(S = n_sim, half_width = 2.75,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = 2.5, start_y = 2.5,
                       seed = 4)),
  .id = "chain")

[1] "Taxa de aceitação 0.28"
[1] "Taxa de aceitação 0.19"
[1] "Taxa de aceitação 0.29"
[1] "Taxa de aceitação 0.15"

Vejam que aqui não estamos interessados em muitas iterações, portanto cada corrente Markov amostrará 100 amostras dando um total de 400 amostras.

Houveram algumas mudanças significativas na taxa de aprovação das propostas Metropolis. Todas ficaram em torno de 15%-29%, isso é por conta do baixo número de amostras (100), caso as amostras fosse maiores veremos esses valores convergirem para próximo de 20% conforme o exemplo anterior de 10.000 amostras com uma única corrente.

Na figura 13 é possível ver as 4 correntes Markov do algoritmo de Metropolis explorando o espaço amostral.

dfs100_met <- Xs_met %>%
  group_by(chain) %>%
  transmute(
    chain,
    iter = 1:n_sim,
    th1 = V1,
    th2 = V2,
    th1l = dplyr::lag(V1, default = V1[1]),
    th2l = dplyr::lag(V2, default = V2[1])
  ) %>%
  ungroup()
p1 <- ggplot(dfs100_met) +
  geom_jitter(width = 0.05, height = 0.05,
              aes(th1, th2, group = chain, color = chain), alpha = 0.3) +
  geom_segment(aes(x = th1, xend = th1l, y = th2, yend = th2l,
                   color = chain)) +
  #geom_point(aes(x = th1, y = th2, color = chain)) +
  stat_ellipse(data = dft, aes(x = X1, y = X2), color = "black", level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Metropolis", subtitle = "100 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_brewer(palette = "Set1") +
  theme(legend.position = "NULL")

animate(p1 +
          transition_reveal(along = iter) +
          shadow_trail(0.01),
        # animation options
        height = 7, width = 7, units = "in", res = 300
)

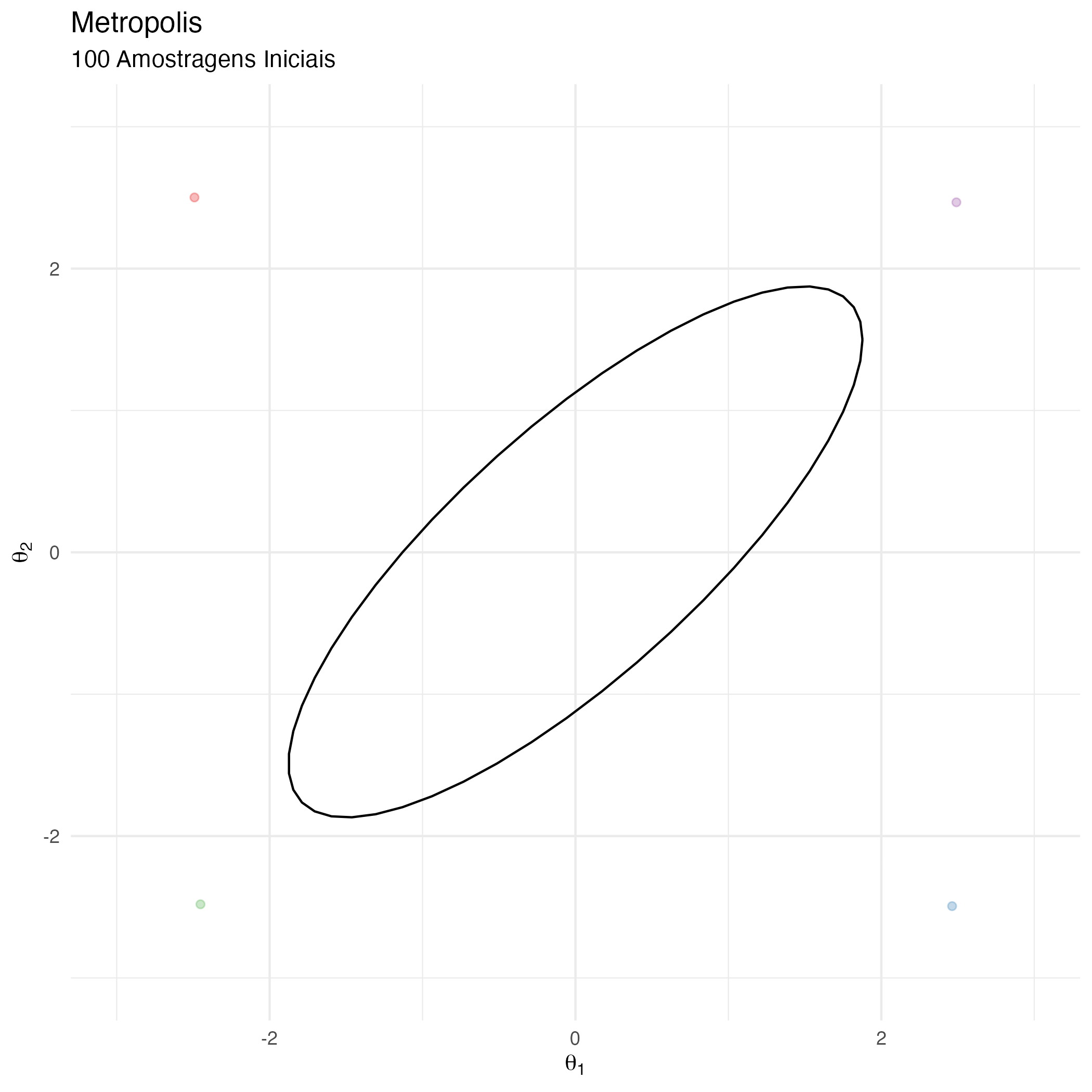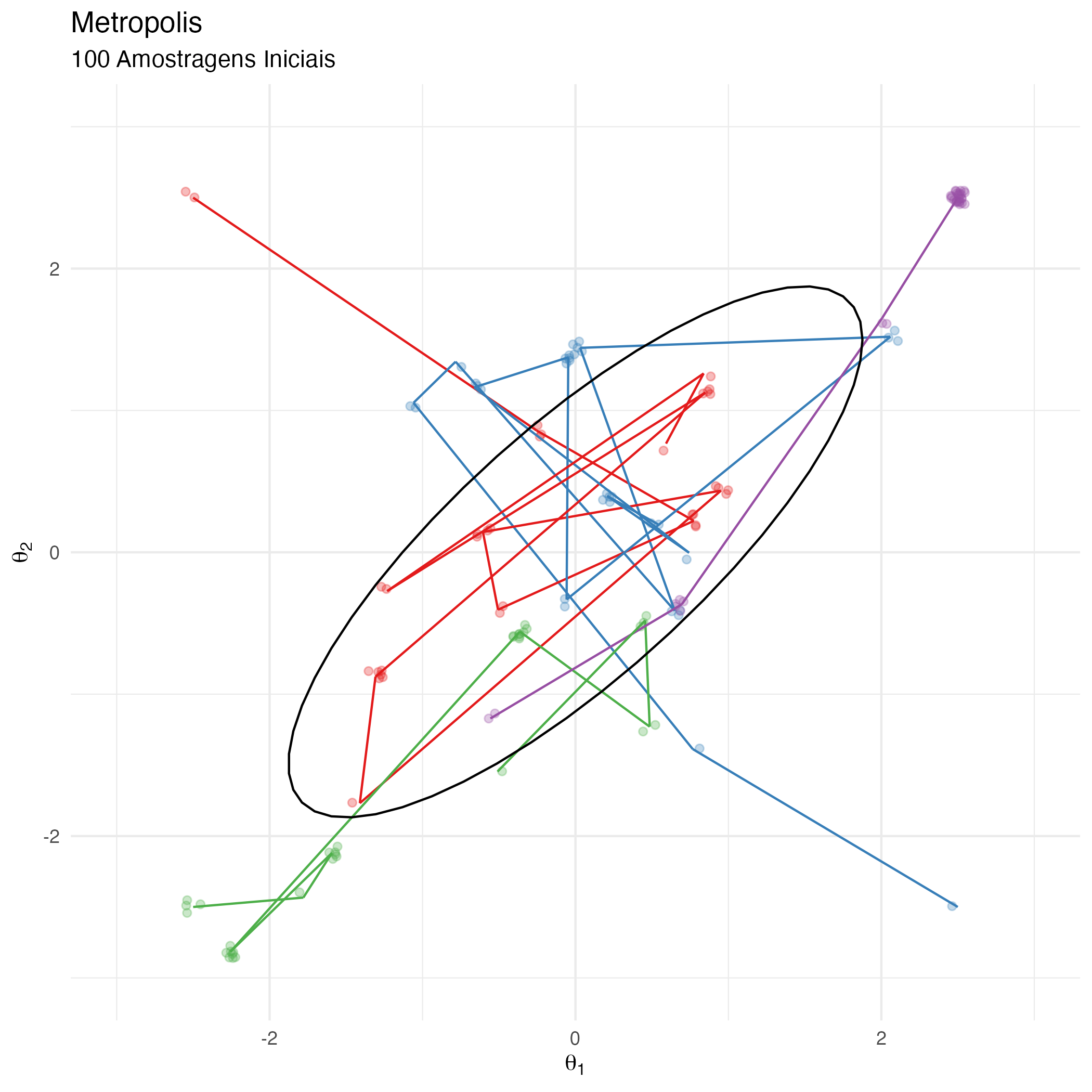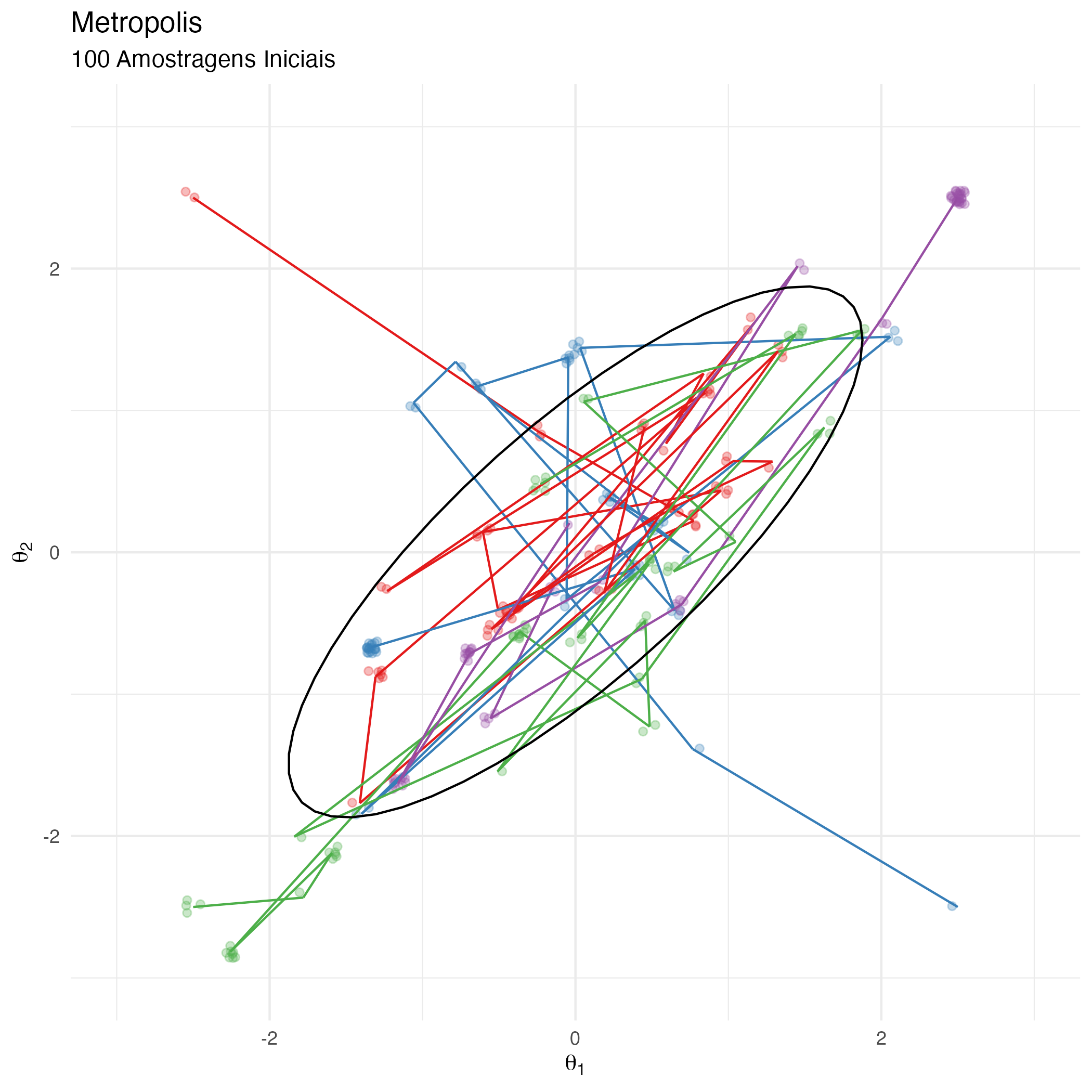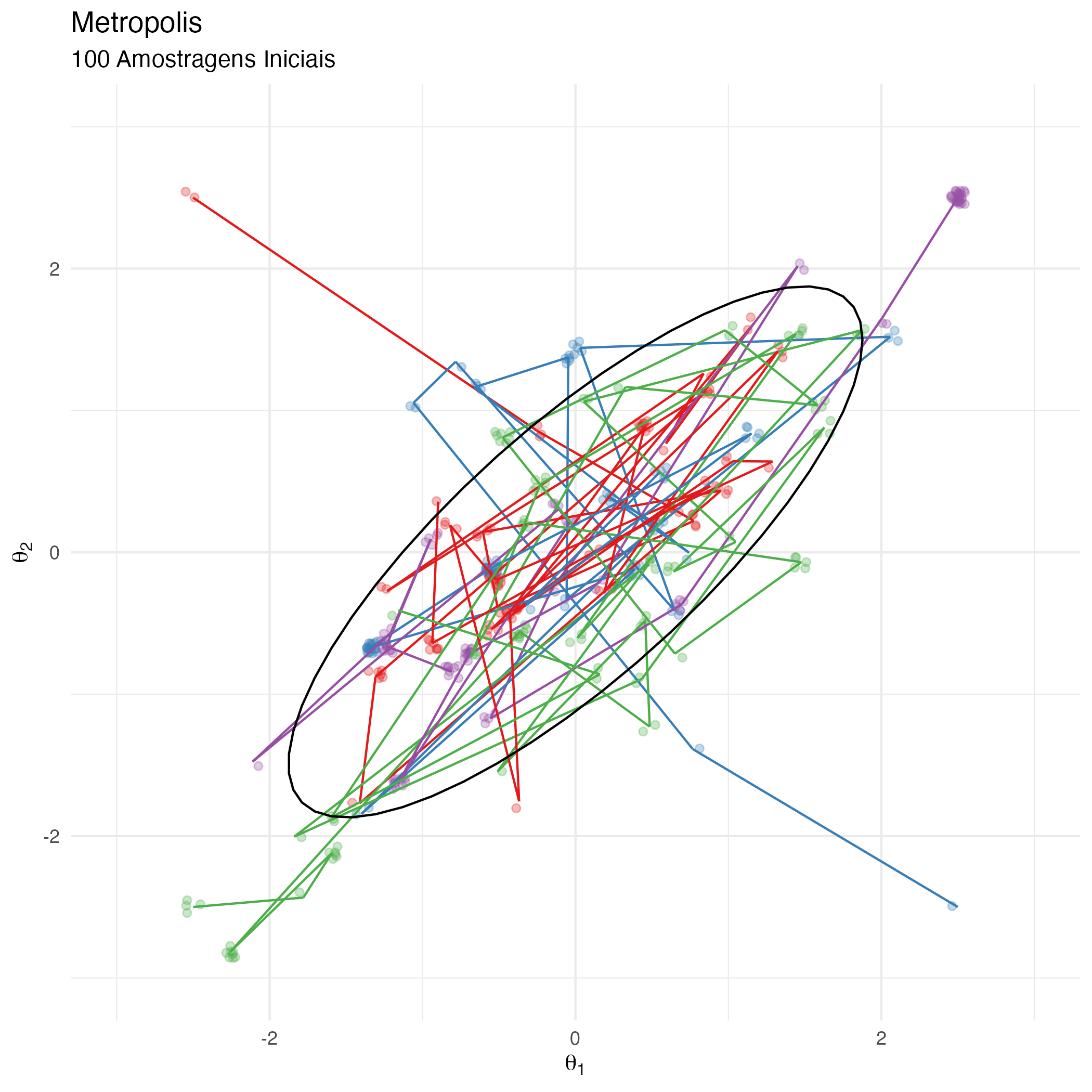
Figure 13: Animação Metropolis – 4 correntes Markov em Paralelo

Correntes Markov em Paralelo – Gibbs

Similar ao exemplo das correntes Markov em paralelo com o algoritmo Metropoli, para criarmos 4 correntes Markov com pontos diferentes de início dos parâmetros, usamos 4 vezes o amostrador Gibbs que codificamos anterior, mas agora passamos diferentes argumentos start_x e start_y, além de diferentes seed do pseudogerador de número aleatórios para termos diferentes comportamentos das correntes Markov. Todo o resultado é combinado em um dataframe com uma coluna id representando o número de cada corrente (de 1 a 4).

Xs_gibbs <- bind_rows(
  as_tibble(gibbs(S = n_sim,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = -2.5, start_y = 2.5,
                       seed = 1)),
  as_tibble(gibbs(S = n_sim,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = 2.5, start_y = -2.5,
                       seed = 2)),
  as_tibble(gibbs(S = n_sim,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = -2.5, start_y = -2.5,
                       seed = 3)),
  as_tibble(gibbs(S = n_sim,
                       mu_X = 0, mu_Y = 0,
                       sigma_X = 1, sigma_Y = 1,
                       rho = r,
                       start_x = 2.5, start_y = 2.5,
                       seed = 4)),
  .id = "chain")

Vejam que aqui não estamos interessados em muitas iterações, portanto cada corrente Markov amostrará 100 amostras dando um total de 400 amostras.

Na figura 14 é possível ver as 4 correntes Markov do algoritmo de Gibbs explorando o espaço amostral.

dfs100_gibbs <- Xs_gibbs %>%
  group_by(chain) %>%
  transmute(
    chain,
    iter = 1:n_sim,
    th1 = V1,
    th2 = V2,
    th1l = dplyr::lag(V1, default = V1[1]),
    th2l = dplyr::lag(V2, default = V2[1])
  ) %>%
  ungroup()
p1 <- ggplot(dfs100_gibbs) +
  geom_point(aes(x = th1, y = th2, group = chain, color = chain)) +
  geom_segment(aes(x = th1, xend = th1l, y = th2, yend = th2l,
                   color = chain)) +
  stat_ellipse(data = dft, aes(x = X1, y = X2), color = "black", level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "Gibbs", subtitle = "100 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_brewer(palette = "Set1") +
  theme(legend.position = "NULL")

animate(p1 +
  transition_reveal(along = iter) +
  shadow_trail(0.01),
  # animation options
  height = 7, width = 7, units = "in", res = 300
)

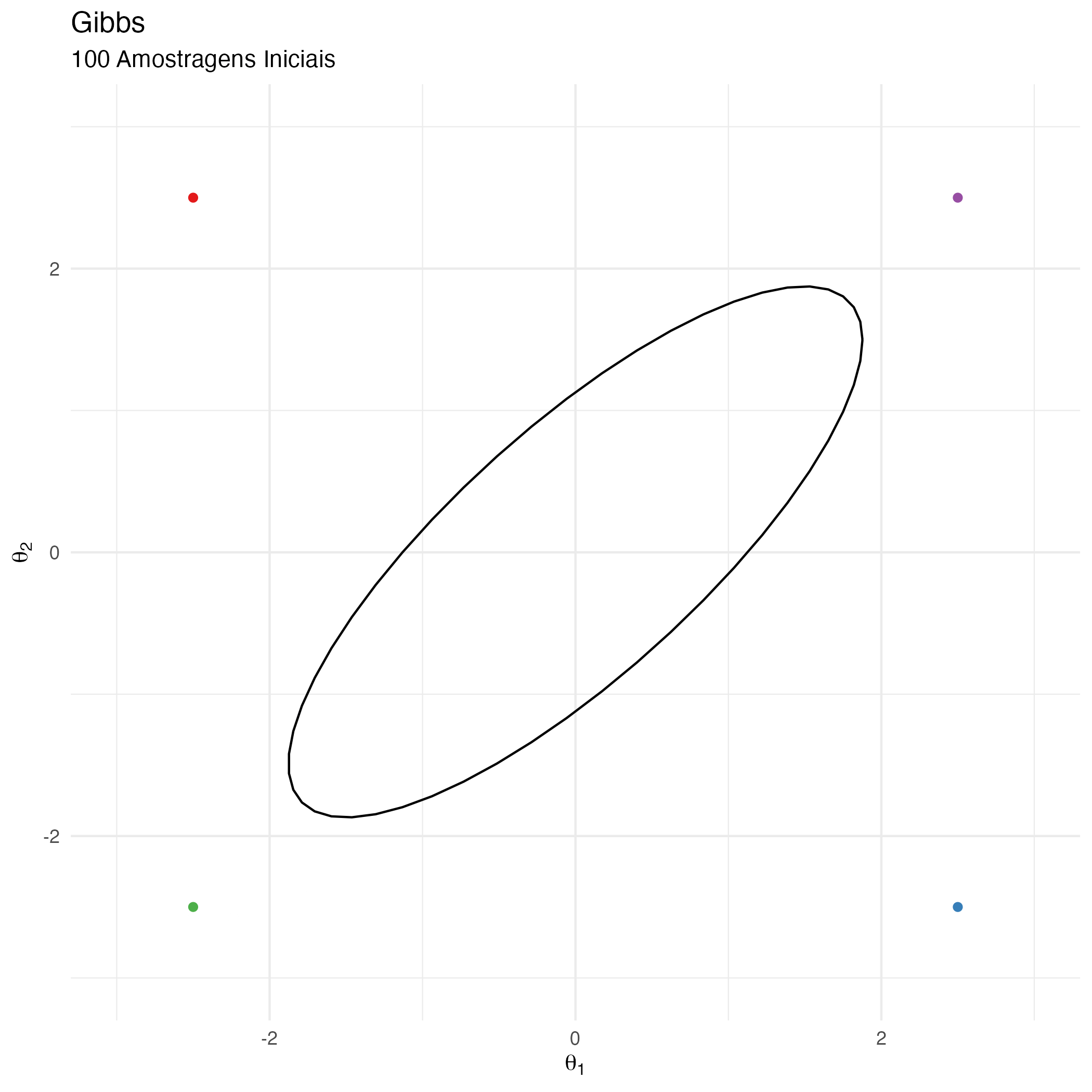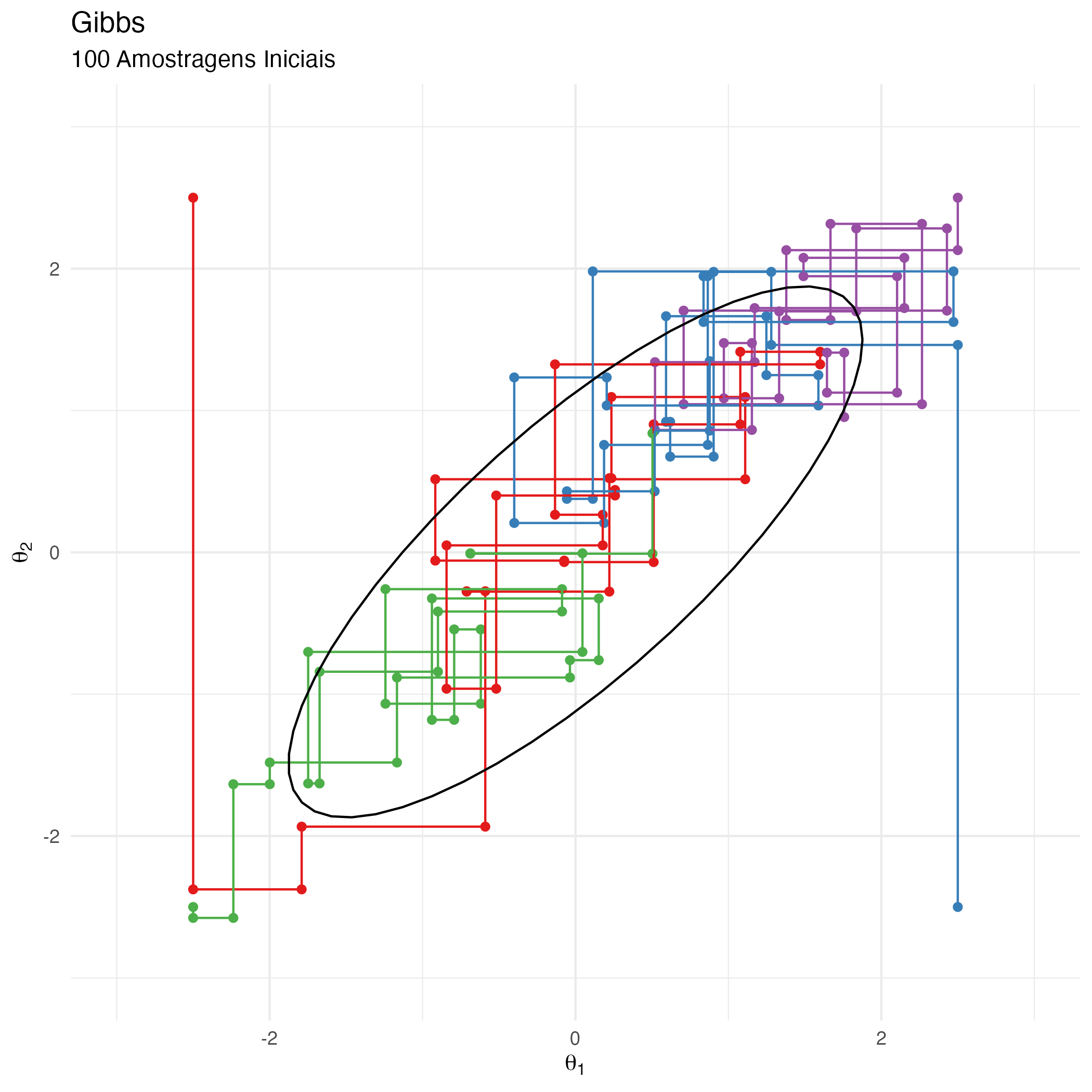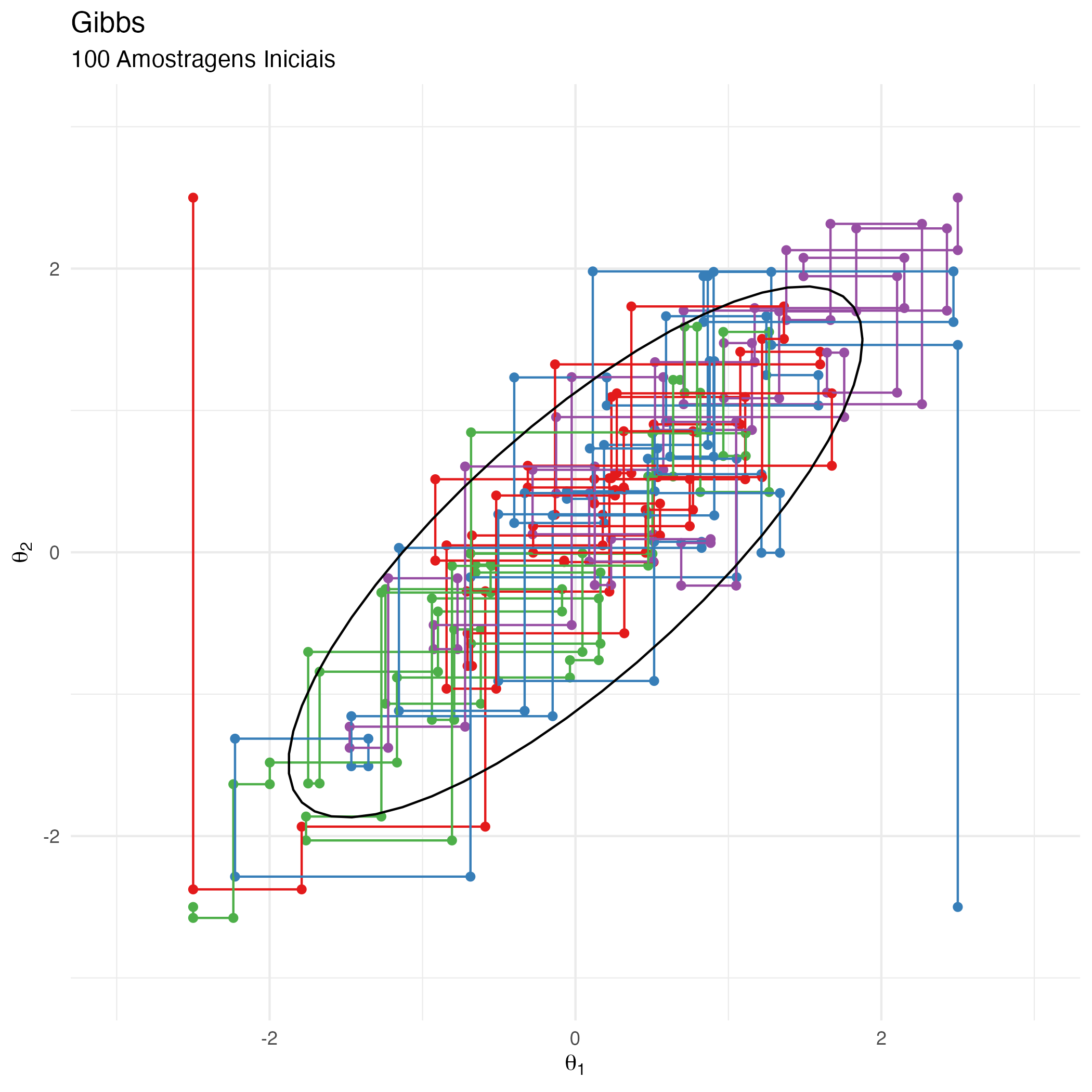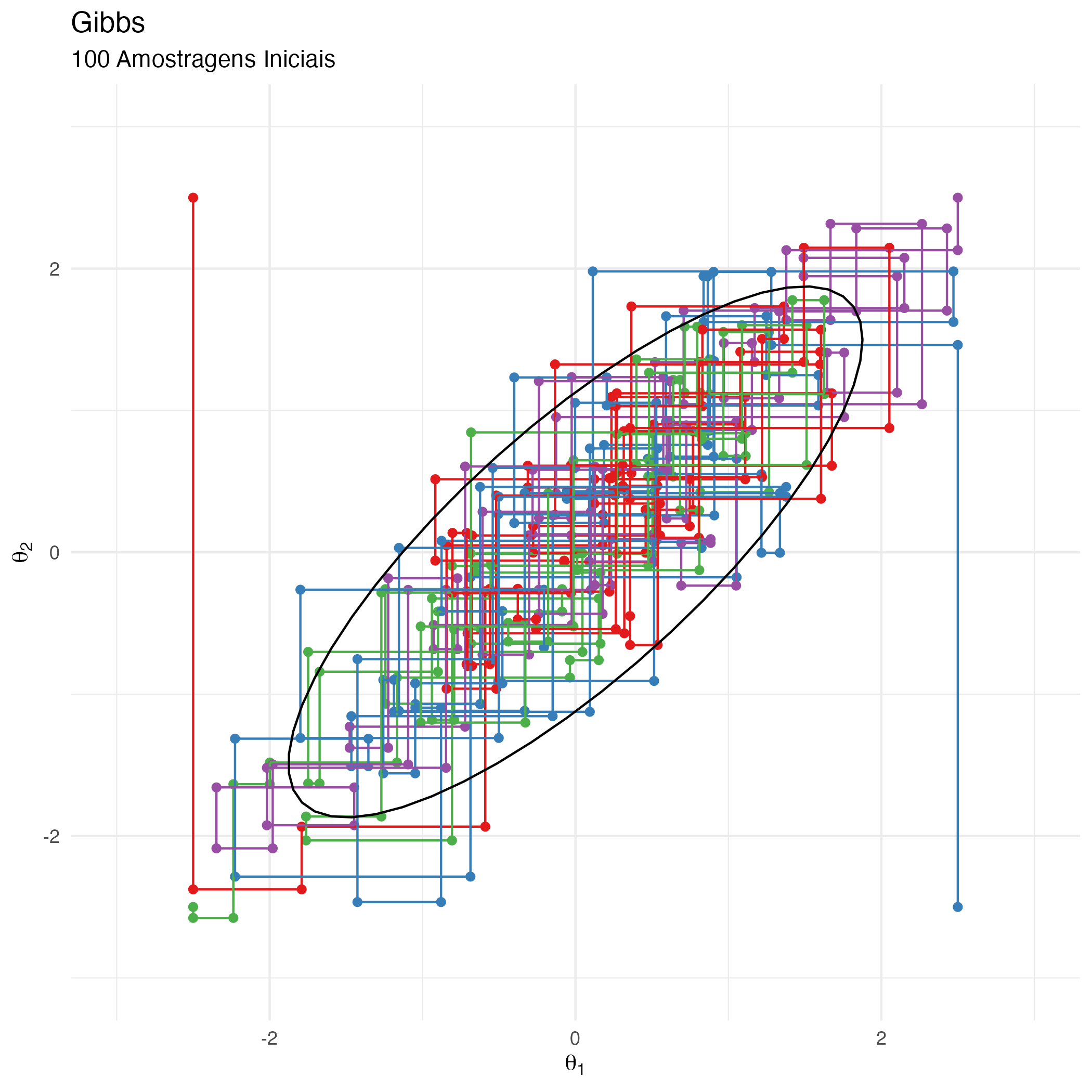
Figure 14: Animação Gibbs – 4 correntes Markov em Paralelo

Hamiltonian Monte Carlo – HMC

Os problemas de baixas taxas de aceitação de propostas das técnicas de Metropolis e do desempenho baixo do algoritmo de Gibbs em problemas multidimensionais nas quais a geometria da posterior é complexa fizeram com que surgisse uma nova técnica MCMC usando dinâmica Hamiltoniana (em homenagem ao físico irlandês William Rowan Hamilton (1805-1865) figura 15). O nome em inglês dessa técnica é Hamiltonian Monte Carlo – HMC.

Figure 15: William Rowan Hamilton. Figura de https://www.wikipedia.org

O HMC é uma adaptação da técnica de Metropolis e emprega um esquema guiado de geração de novas proposta: isso melhora a taxa de aceitação de propostas e, consequentemente, a eficiência. Mais especificamente, o HMC usa o gradiente do log da posterior para direcionar a cadeia de Markov para regiões de maior densidade posterior, onde a maioria das amostras são coletadas. Como resultado, uma corrente Markov com o algoritmo HMC bem ajustada aceitará propostas em uma taxa muito mais alta do que o algoritmo Metropolis tradicional (Beskos et al., 2013; Roberts et al., 1997).

HMC foi inicialmente descrito na literatura de física Duane, Kennedy, Pendleton, & Roweth (1987) (que chamaram de “hybrid” Monte Carlo – HMC). Logo depois, HMC foi aplicado a problemas estatísticos por Radford M. Neal (1994) (que chamou de Hamiltonean Monte Carlo – HMC). Para uma discussão aprofundada (que não é o foco deste conteúdo) de HMC eu recomendo Radford M. Neal (2011) e Betancourt (2017).

HMC usa dinâmica Hamiltoniana aplicada para partículas explorando a geometria de uma probabilidade posterior. Em algumas simulações Metropolis possui taxa de aceitação de aproximadamente 23%, enquanto HMC 65% (Beskos et al., 2013; Gelman et al., 2013b). Além de explorar melhor a geometria da posterior e tolerar geometrias complexas, HMC é muito mais eficiente que Metropolis e não sofre do problema de correlação dos parâmetros que Gibbs.

Para cada componente \(\theta_j\), o HMC adiciona uma variável de momento \(\phi_j\). A densidade posterior \(P(\boldsymbol{\theta} \mid y)\) é incrementada por uma distribuição independente \(P(\boldsymbol{\phi})\) dos momentos, definindo assim uma distribuição conjunta:

\[ P(\boldsymbol{\theta}, \boldsymbol{\phi} \mid y) = P(\boldsymbol{\phi}) \cdot P(\boldsymbol{\theta} \mid y) \]

O HMC usa uma distribuição de propostas que muda dependendo do estado atual na corrente Markov. O HMC descobre a direção em que a distribuição posterior aumenta, chamada de gradiente, e distorce a distribuição de propostas em direção ao gradiente. No algoritmo de Metropolis, a distribuição das propostas seria uma distribuição Normal (geralmente) centrada na posição atual, de modo que saltos acima ou abaixo da posição atual teriam a mesma probabilidade de serem propostos. Mas o HMC gera propostas de maneira bem diferente.

Você pode imaginar que para distribuições posteriores de alta dimensão que têm vales diagonais estreitos e até mesmo vales curvos, a dinâmica do HMC encontrará posições propostas que são muito mais promissoras do que uma distribuição de proposta simétrica ingênua, e mais promissoras do que a amostragem de Gibbs, que pode obter preso em paredes diagonais.

A probabilidade da corrente Markov mudar de estado no algoritmo HMC é definida como:

\[ P_{\text{mudar}} = \min\left({\frac{P(\boldsymbol{\theta}_{\text{proposto}}) \cdot P(\boldsymbol{\phi}_{\text{proposto}})}{P(\boldsymbol{\theta}_{\text{atual}})\cdot P(\boldsymbol{\phi}_{\text{atual}})}}, 1\right), \]

onde \(\boldsymbol{\phi}\) é o momento.

Distribuição dos Momentos – \(P(\boldsymbol{\phi})\)

Normalmente damos a \(\boldsymbol{\phi}\) uma distribuição normal multivariada com média 0 e covariância de \(\mathbf{M}\), uma “matriz de massa.” Para mantêr as coisas um pouco mais simples, usamos uma matriz de massa diagonal \(\mathbf{M}\). Isso faz com que os componentes de \(\boldsymbol{\phi}\) sejam independentes com \(\phi_j \sim \text{Normal}(0, M_{jj})\)

Algoritmo de HMC

O algoritmo de HMC é bem similar ao algoritmo Metropolis mas com a inclusão do momento \(\boldsymbol{\phi}\) como uma maneira de quantificar o gradiente da posterior.

1. Defina um ponto inicial \(\boldsymbol{\theta}^{(0)} \in \mathbb{R}^p\) do qual \(P\left(\boldsymbol{\theta}^{(0)} \mid y \right) > 0\)

2. Amostre \(\boldsymbol{\phi}\) de uma \(\text{Normal}(\mathbf{0},\mathbf{M})\)

3. Simultaneamente amostre \(\boldsymbol{\theta}\) e \(\boldsymbol{\phi}\) com \(L\) leapfrog steps (não sei como traduzir isso, talvez múltiplos passos) cada um reduzido por um fator \(\epsilon\). Em um leapfrog step, tanto \(\boldsymbol{\theta}\) quanto \(\boldsymbol{\phi}\) são alterados, um em relação ao outro. Repita os seguintes passos \(L\) vezes:

   1. Use o gradiente do log da posterior⁹ de \(\boldsymbol{\theta}\) para produzir um meio-salto(half-step) de \(\boldsymbol{\phi}\):

      \[\boldsymbol{\phi} \leftarrow \boldsymbol{\phi} + \frac{1}{2} \epsilon \frac{d \log P(\boldsymbol{\theta} \mid y)}{d \theta}\]

   2. Use o vetor de momentos \(\boldsymbol{\phi}\) para atualizar o vetor de parâmetros \(\boldsymbol{\theta}\):

      \[\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} + \epsilon \mathbf{M}^{-1} \boldsymbol{\phi}\]

   3. Novamente use o gradiente de \(\boldsymbol{\theta}\) para produzir um meio-salto(half-step) de \(\boldsymbol{\phi}\):

      \[\boldsymbol{\phi} \leftarrow \boldsymbol{\phi} + \frac{1}{2} \epsilon \frac{d \log P(\boldsymbol{\theta} \mid y)}{d \theta}\]

4. Designe \(\boldsymbol{\theta}^{(t-1)}\) e \(\boldsymbol{\phi}^{(t-1)}\) como os valores do vetor de parâmetros e do vetor de momentos, respectivamente, no início do processo de leapfrog (etapa 2) e \(\boldsymbol{\theta}^{(*)}\) e \(\boldsymbol{\phi}^{(*)}\) como os valores após \(L\) passos. Como regra de aceitação/rejeição calcule:

   \[r = \frac{P \left(\boldsymbol{\theta}^{(*)} \mid y \right) P \left(\boldsymbol{\phi}^{(*)} \right)}{P \left(\boldsymbol{\theta}^{(t-1)} \mid y \right) P \left(\boldsymbol{\phi}^{(t-1)} \right)}\]

5. Designe:

   \[\boldsymbol{\theta}^{(t)} = \begin{cases} \boldsymbol{\theta}^{(*)} & \text{com probabilidade $\min(r,1)$}\\ \boldsymbol{\theta}^{(t-1)} & \text{caso contrário} \end{cases}\]

HMC – Implementação

Para HMC, não vou codificar o algoritmo na mão, pois envolve derivadas que não vai ser muito eficiente no R. Para isso temos o Stan. O arquivo hmc.rds possui 1.000 amostragens com um leapfrog \(L = 40\), então no total são 40.001 iterações¹⁰. O exemplo é o mesmo que usamos para Metropolis e Gibbs, uma distribuição normal multivariada de \(X\) e \(Y\) (ambos com média 0 e desvio padrão 1), com correlação 0.8 (\(\rho = 0.8\)):

\[ \begin{bmatrix} X \\ Y \end{bmatrix} \sim \text{Normal Multivariada} \left( \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \mathbf{\Sigma} \right) \\ \mathbf{\Sigma} \sim \begin{pmatrix} 1 & 0.8 \\ 0.8 & 1 \end{pmatrix} \]

load(here::here("R", "hmc.RData"))
df <- tibble(id = rep(1, 40000),
                 iter = rep(1:1000, each = 40),
                 th1 = tt[1:40000, 1],
                 th2 = tt[1:40000, 2],
                 th1l = c(tt[1, 1], tt[1:(40000 - 1), 1]),
                 th2l = c(tt[1, 2], tt[1:(40000 - 1), 2]))

X_hmc <- tt[seq(2, 40001, by = 40), ]
res <- monitor(X_hmc, digits_summary = 1)

Inference for the input samples (2 chains: each with iter = 1000; warmup = 500):

     Q5  Q50 Q95 Mean  SD  Rhat Bulk_ESS Tail_ESS
V1 -1.6 -0.1 1.4 -0.1 0.9     1      604      655

For each parameter, Bulk_ESS and Tail_ESS are crude measures of 
effective sample size for bulk and tail quantities respectively (an ESS > 100 
per chain is considered good), and Rhat is the potential scale reduction 
factor on rank normalized split chains (at convergence, Rhat <= 1.05).

neff <- res[, "n_eff"]
reff <- mean(neff / (nrow(X_hmc))) #  61%!!!

Na nossa execução do algoritmo HMC temos como resultado uma matriz X_hmc com 100 linhas e 2 colunas (as mesmas condições já mostradas nos exemplos anteriores com algoritmo Metropolis e Gibbs, porém agora somente com 1.000 amostras).

Vejam que o número de amostras eficientes em relação ao número total de iterações reff é 61% para todas as iterações incluindo warm-up (no caso 1 leapfrog step \(L = 1\)). A eficiência do algoritmo HMC, no nosso exemplo didático, é o mais que 6x a eficiência do algoritmo de Metropolis (9,5% vs 61%) e quase 3x a eficiência do Gibbs (23% vs 61%).

HMC – Intuição Visual

A animação na figura 16 mostra as 50 primeiras simulações do algoritmo HMC usado para gerar X_hmc. Vejam que aqui temos em amarelo temos os leapfrog steps moldandos e distorcendo a distribuição de propostas em direção ao gradiente da posterior (conduzindo-as para áreas de maior probabilidade da posterior) e em vermelho temos as amostras após os 40 leapfrog step \(L = 40\) de cada interação. Notem como a exploração da posterior é muito mais eficiente e focada em locais onde realmente a distribuição de interesse possui maior probabilidade.

labs3 <- c("Amostras", "Iterações do Algoritmo", "90% HPD", "Leapfrog")
# base plot
p0 <- ggplot() +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "3"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "HMC", subtitle = "50 Amostragens Iniciais",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("red", "forestgreen", "blue", "yellow"), labels = labs3) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA, NA, 16), linetype = c(0, 1, 1, 0)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

# first 100 iterations
df50 <- df %>% filter(iter <= 50)
pp <- p0 + geom_point(data = df50,
                      aes(th1, th2, color = "4"), alpha = 0.3, size = 1) +
  geom_segment(data = df50,
               aes(x = th1, xend = th1l, color = "2", y = th2, yend = th2l),
               alpha = 0.5) +
        geom_point(data = df50[seq(1, nrow(df50), by = 40), ],
                   aes(th1, th2, color = "1"), size = 2)

animate(pp +
  transition_manual(iter, cumulative = TRUE) +
  shadow_trail(0.05),
  # animation options
  height = 7, width = 7, units = "in", res = 300
)

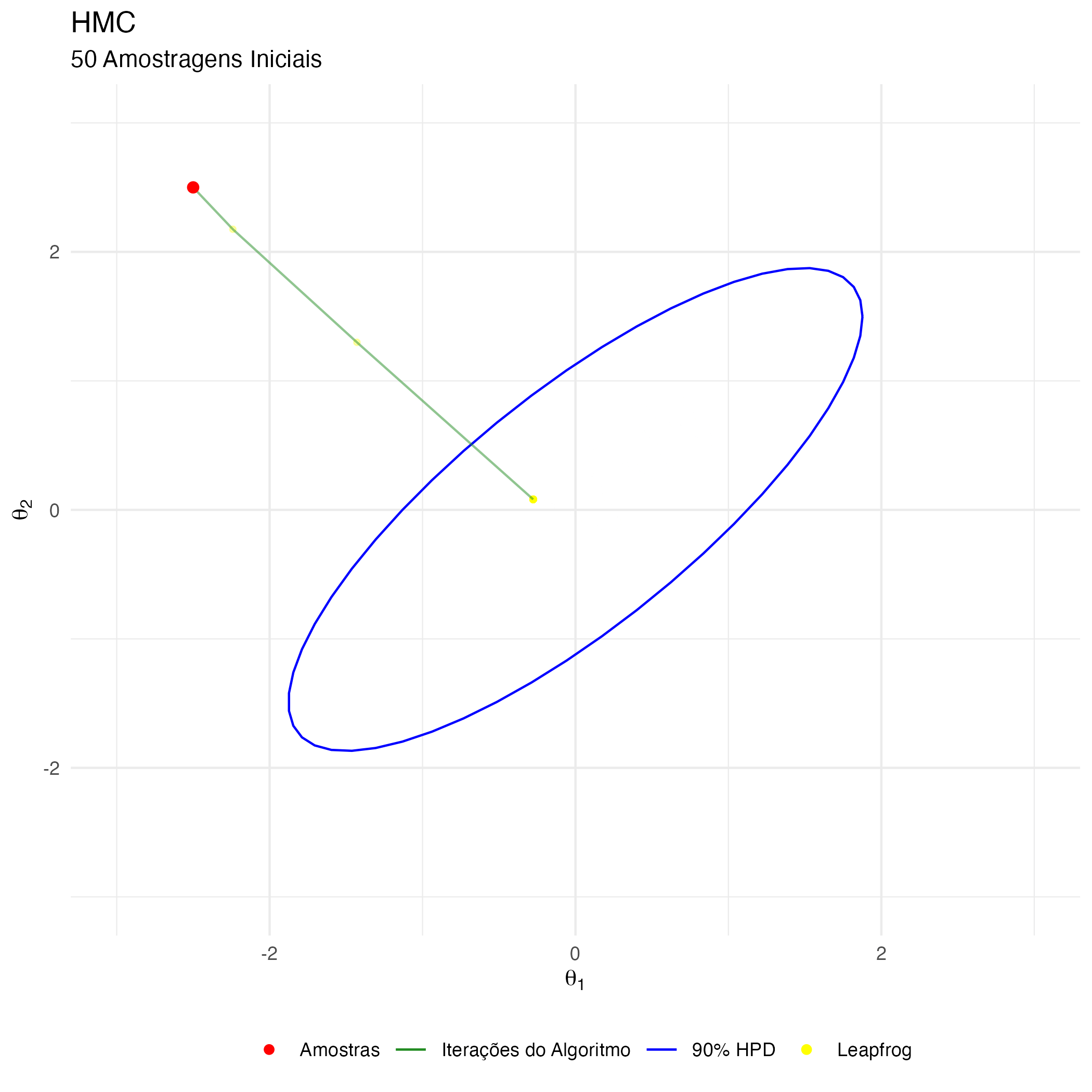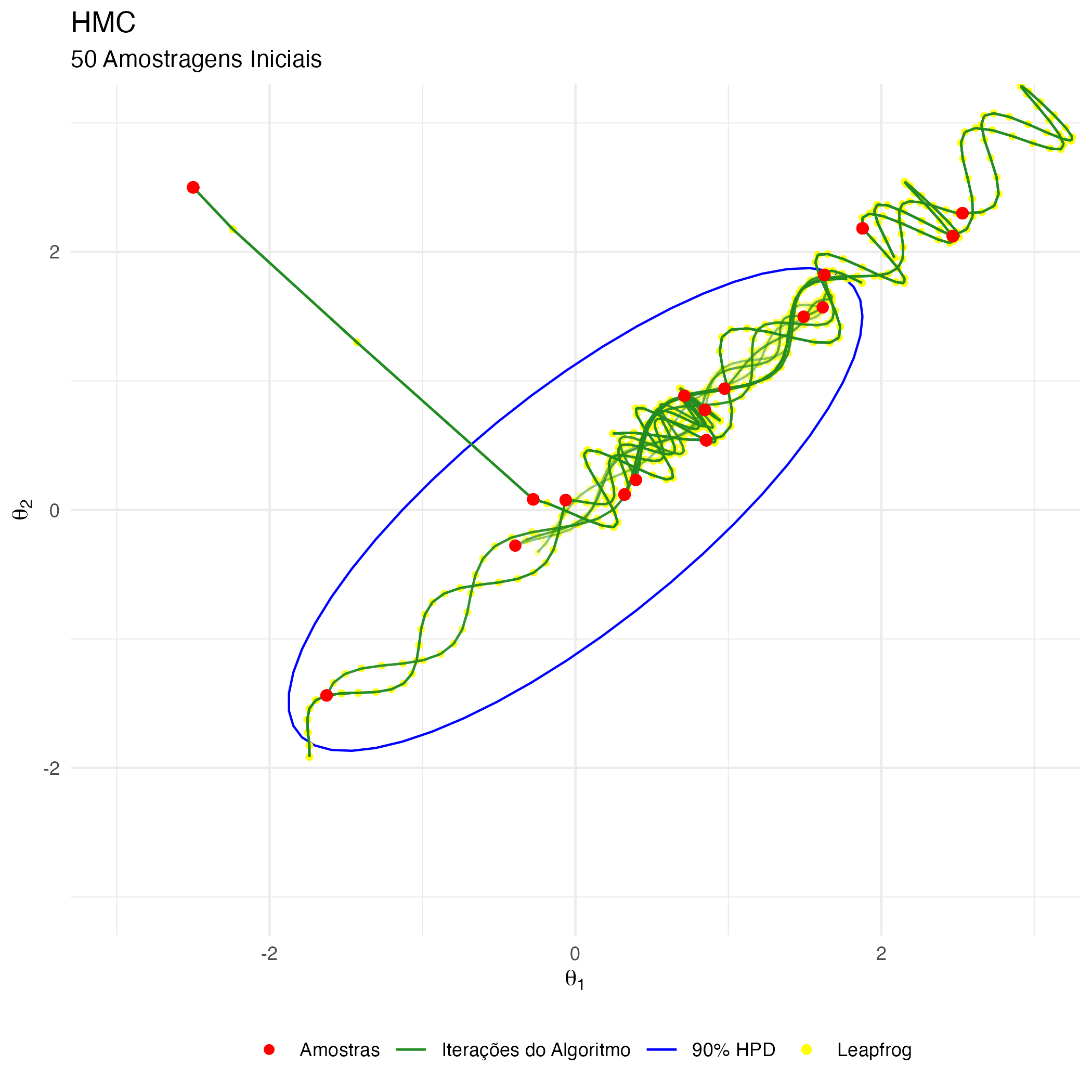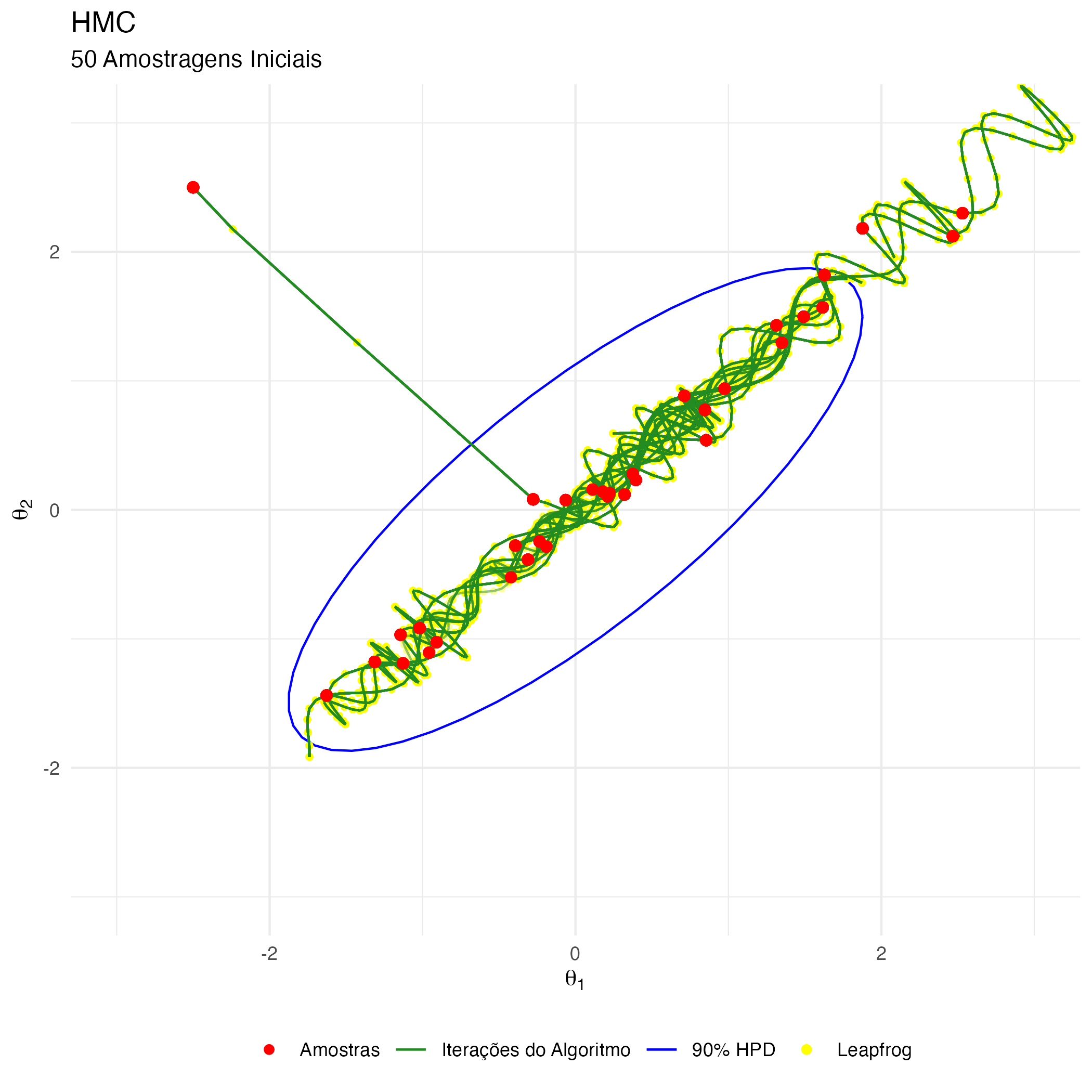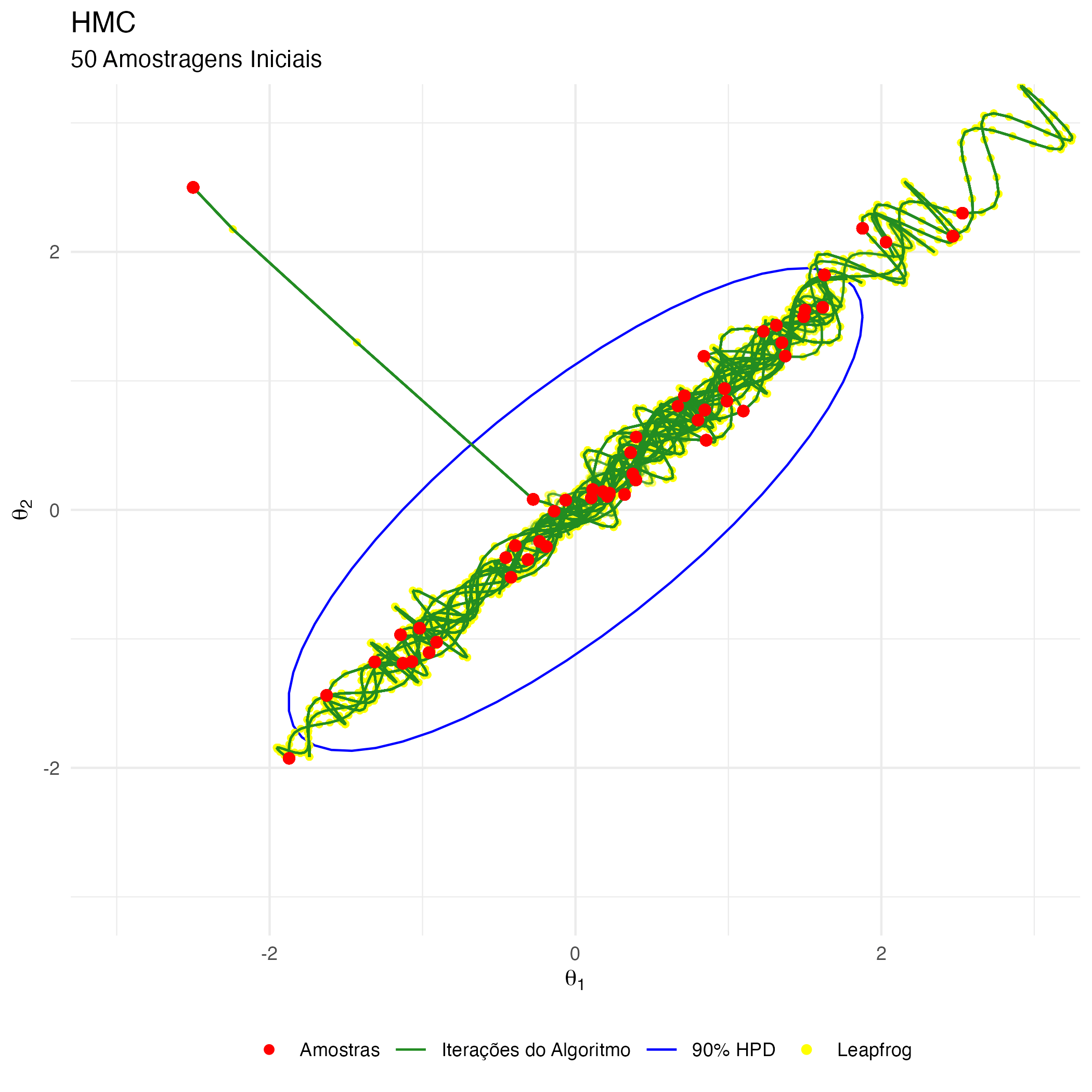
Figure 16: Animação HMC

Na figura 17 é possível ver como ficaram as 1.000 simulações excluindo o primeiro leapfrog step \(L = 1\) como warmup.

# Take all the 1,000 observations after warmup of 1,000
warm <- 1
dfs <- data.frame(
  th1 = tt[(warm + 1):nrow(tt), 1],
  th2 = tt[(warm + 1):nrow(tt), 2]
)

ggplot() +
  geom_point(data = dfs[seq(1, nrow(dfs), by = 40), ],
             aes(th1, th2, color = "1"), alpha = 0.3) +
  stat_ellipse(data = dft, aes(x = X1, y = X2, color = "2"), level = 0.9) +
  coord_cartesian(xlim = c(-3, 3), ylim = c(-3, 3)) +
  labs(
    title = "HMC", subtitle = "1.000 Amostragens",
    x = expression(theta[1]), y = expression(theta[2])) +
  scale_color_manual(values = c("steelblue", "blue"), labels = labs2) +
  guides(color = guide_legend(override.aes = list(
    shape = c(16, NA), linetype = c(0, 1), alpha = c(1, 1)))) +
  theme(legend.position = "bottom", legend.title = element_blank())

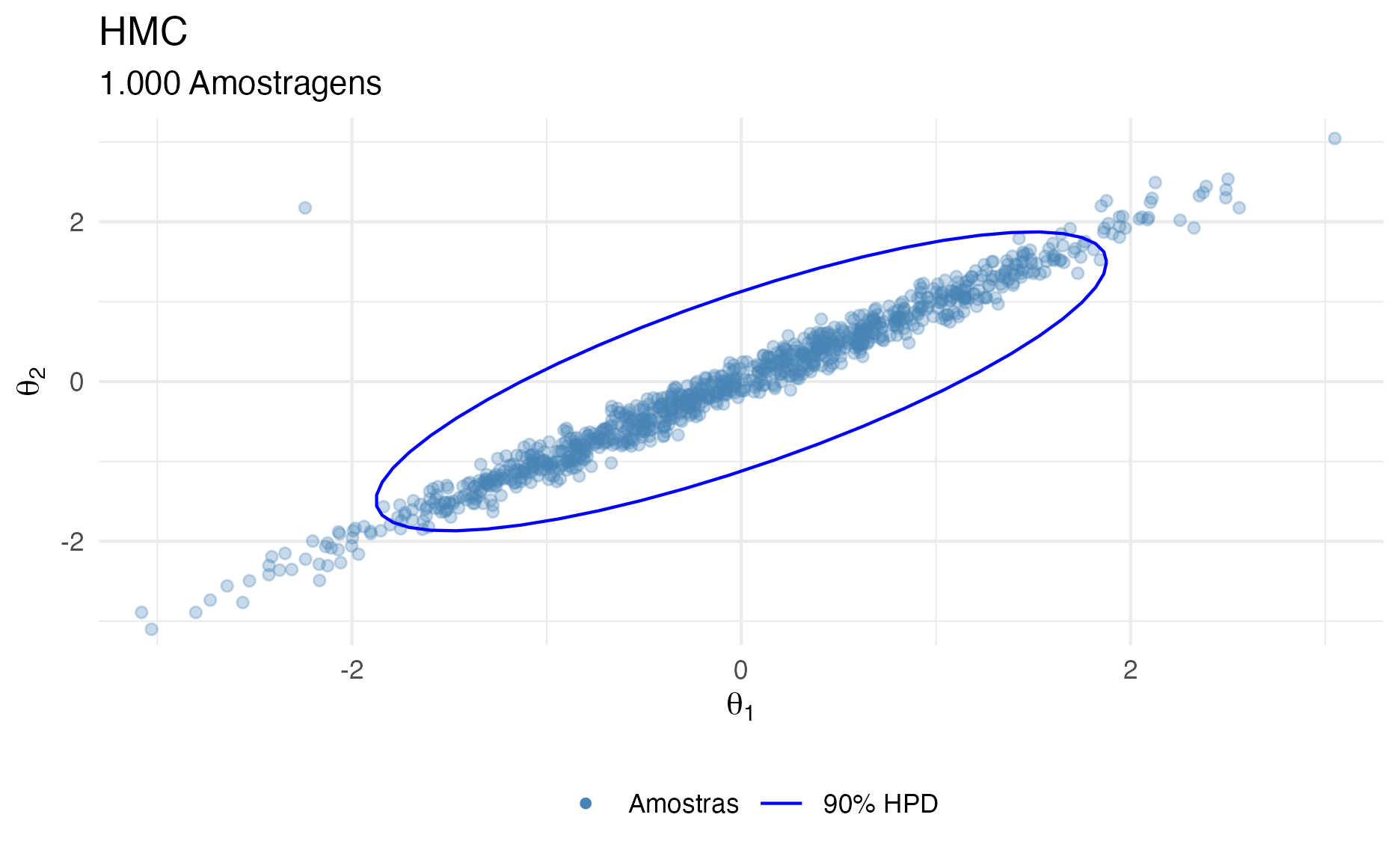
Figure 17: 1.000 simulações HMC após descarte da primeira iteração como warmup

HMC – Geometrias Complexas

Há casos que HMC será muito melhor que Metropolis ou Gibbs. Em especial, esses casos se concentram em geometrias complicadas e de difícil exploração. Nesses contextos um algoritmo que consiga guiar as propostas para regiões de maior densidade (como é o caso do HMC) consegue explorar de maneira muito mais eficiente (menos iterações para convergência) e eficaz (maior taxa de aceitação das propostas).

Veja na figura 18 um exemplo de uma posterior bimodal (destaque para o histograma marginal de \(X\) e \(Y\)):

\[ X = \text{Normal} \left( \begin{bmatrix} 10 \\ 2 \end{bmatrix}, \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right), \quad Y = \text{Normal} \left( \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 8.4 & 2.0 \\ 2.0 & 1.7 \end{bmatrix} \right). \]

library(ggExtra)
components <- sample(1:2, prob = c(0.5, 0.5), size = N, replace = TRUE)

mus_1 <- c(10, 2)
sds_1 <- sqrt(c(1, 1))
samples_1 <- rnorm(n = N, mean = mus_1[components], sd = sds_1[components])


mus_2 <- c(0, 0)
sds_2 <- sqrt(c(8.4, 1.7))
samples_2 <- rnorm(n = N, mean = mus_2[components], sd = sds_2[components])

dft_bimodal <- data.frame(samples_1, samples_2)

p4 <- ggplot(dft_bimodal, aes(samples_1, samples_2)) +
  geom_point() +
  labs(title = "Multivariada Normal",
           subtitle = "Mistura de uma Normal Bimodal com uma Normal com cauda longa",
           caption = "10.000 simulações",
           x = expression(X), y = expression(Y)) +
      theme(legend.position = "NULL")
ggMarginal(p4, type = "density")

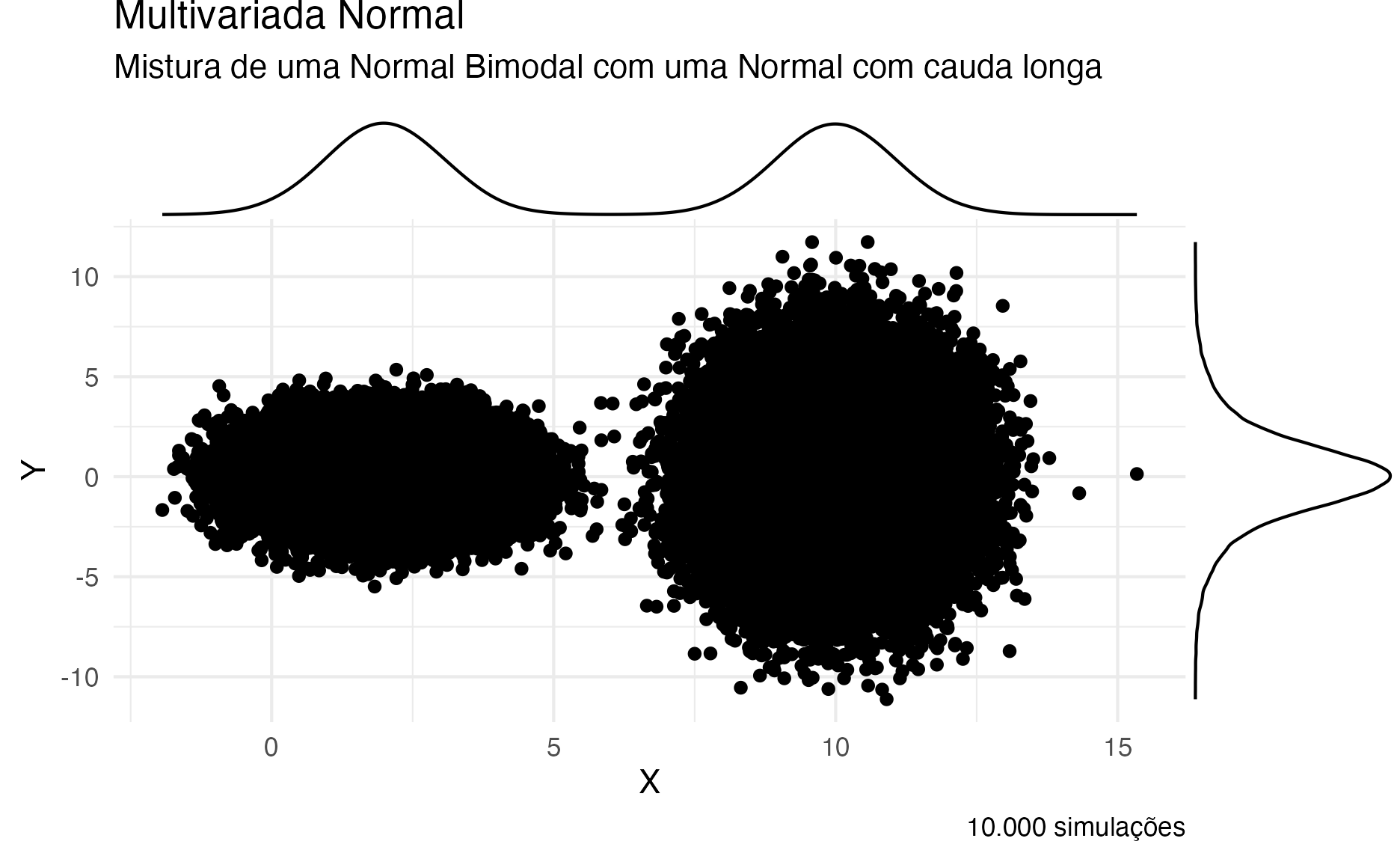
Figure 18: Gráfico de Densidade de uma distribuição Multivariada Normal com Multimodalidade

E para finalizar um exemplo do funil de Neal (Radford M. Neal, 2003) na figura 19. Essa é uma posterior bem difícil de ser amostrada até mesmo para HMC, pois ela varia de geometria nas dimensões \(X\) e \(Y\). Isso faz com que o amostrador HMC tenha que toda hora trocar o leapfrog steps \(L\) e o fator \(\epsilon\), pois na parte superior da imagem (o topo do funil) são necessários um valor de \(L\) grande e \(\epsilon\) um valor pequeno; e na parte de baixo (no fundo do funil) o contrário: \(L\) pequeno e \(\epsilon\) grande.

y <- rnorm(N, 0, 3)
x <- rnorm(N, 0, exp(y / 2))
dft_funnel <- data.frame(x, y)

ggplot(dft_funnel, aes(x, y)) +
  geom_point() +
  labs(title = "Funil de Neal",
           caption = "10.000 simulações",
           x = expression(X), y = expression(Y)) +
      theme(legend.position = "NULL")

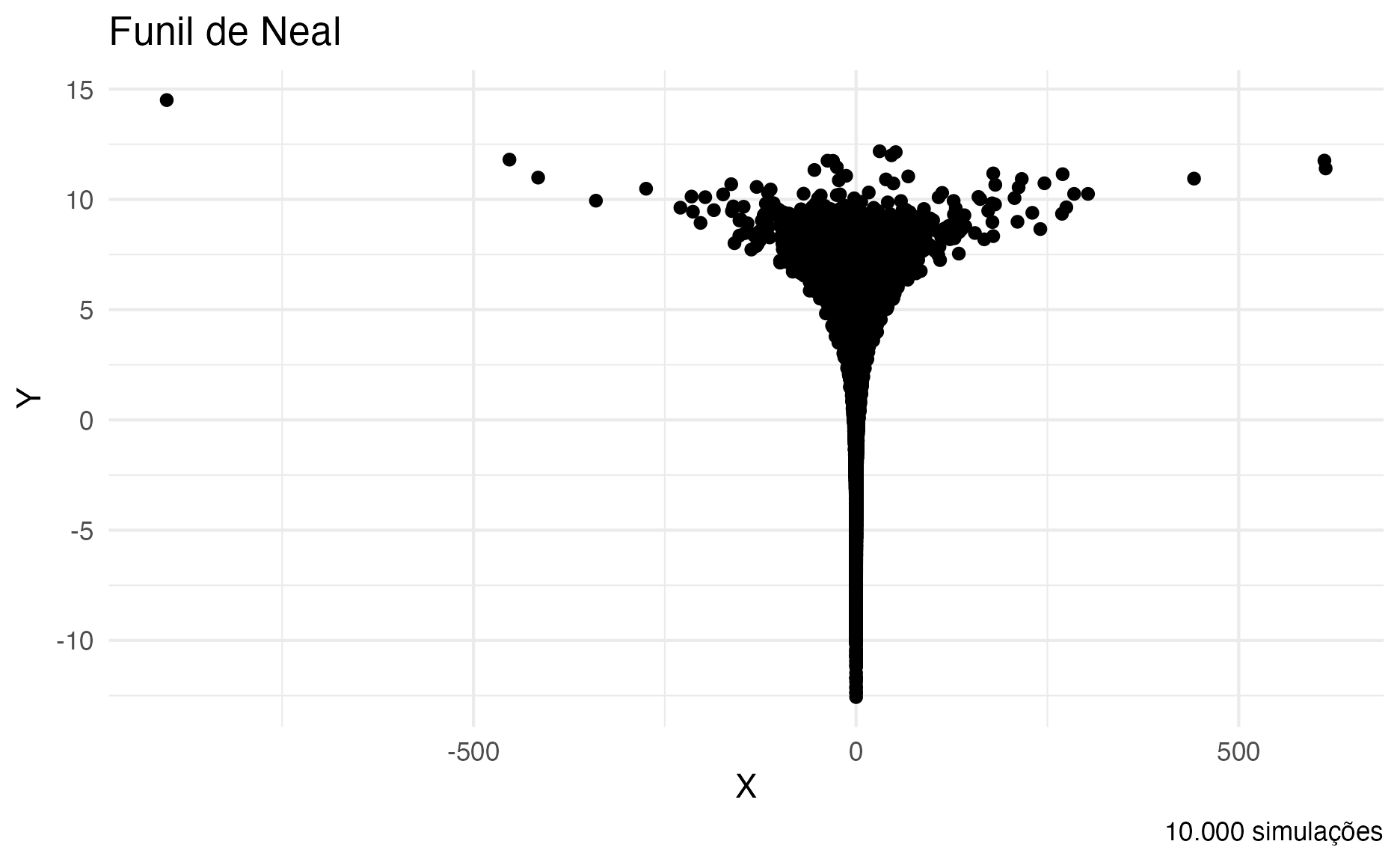
Figure 19: Gráfico de Densidade do Funil de Neal

“Não entendi nada…”

Se você não entendeu nada até agora, não se desespere. Pule todas as fórmulas e pegue a intuição visual dos algoritmos. Veja as limitações de Metropolis e Gibbs e compare as animações e figuras com as do HMC. A superioridade de eficiência (mais amostras com baixa autocorrelação) e eficácia (mais amostras próximas das áreas de maior probabilidade da distribuição-alvo) é autoexplicativa pelas imagens.

Além disso, você provavelmente nunca terá que codificar o seu algoritmo HMC (Gibbs, Metropolis ou qualquer outro MCMC) na mão. Para isso há pacotes como Stan (e seu ecossistema de pacotes: rstan, PyStan, brms, rstanarm, Stan.jl etc.). Além disso, Stan implementa um HMC modificado com uma técnica chamada No-U-Turn Sampling (NUTS)¹¹ (Hoffman & Gelman, 2011) que seleciona automaticamente os valores de \(\epsilon\) (fator de redução) e \(L\) (quantidade de leapfrog steps).¹² O desempenho do HMC é altamente sensível à esses dois “hiperparâmetros” (parâmetros que devem ser especificados pelo usuário). Em particular, se \(L\) for muito pequeno, o algoritmo exibe comportamento indesejável de um passeio aleatório, enquanto se \(L\) for muito grande, o algoritmo desperdiça eficiência computacional. NUTS usa um algoritmo recursivo para construir um conjunto de pontos candidatos prováveis que abrangem uma ampla faixa da distribuição de propostas, parando automaticamente quando começa a voltar e refazer seus passos (por isso que ele não dá meia-volta – No U-turn), adicionalmente NUTS também calibra automaticamente (e de maneira simultânea) \(L\) e \(\epsilon\).

Implementação com o rstanarm

Como configuração padrão, o pacote rstanarm utiliza HMC com NUTS. Além disso, os argumentos padrões do HMC no rstanarm são:

• 4 correntes Markov de amostragem (chains = 4); e
• 2.000 iterações de cada corrente (iter = 2000)¹³.

Relembrando o exemplo da aula de regressão linear, vamos usar o mesmo dataset kidiq. São dados de uma survey de mulheres adultas norte-americanas e seus respectivos filhos. Datado de 2007 possui 434 observações e 4 variáveis:

• kid_score: QI da criança;
• mom_hs: binária (0 ou 1) se a mãe possui diploma de ensino médio;
• mom_iq: QI da mãe; e
• mom_age: idade da mãe.

Vamos estimar um modelo de regressão linear Bayesiano na qual a variável dependente é kid_score e as independentes são mom_hs e mom_iq.

O modelo é o especificado da seguinte maneira:

\[ \begin{aligned} \alpha &\sim \text{Normal}(\mu_y, s_y) \\ \beta_k &\sim \text{Normal}(0, 2.5 \cdot \frac{s_y}{s_x}) \\ \sigma &\sim \text{Exponencial}(\frac{1}{s_y})\\ y &\sim \text{Normal}(\alpha + \beta_1 x_1 + \dots + \beta_K x_K, \sigma), \end{aligned} \]

onde \(s_x = \tt{sd(x)}\), \[ s_y = \begin{cases} \tt{sd(y)} & \text{se } \tt{family = gaussian}, \\ 1 & \text{caso contrário}. \end{cases} \] e \[ \mu_y = \begin{cases} \tt{mean(y)} & \text{se } \tt{family = gaussian}, \\ 0 & \text{caso contrário}. \end{cases} \]

No caso temos apenas duas variáveis independentes, então \(K=2\) e \(\beta_1 = \tt{mom\_hs}\) e \(\beta_2 = \tt{mom\_iq}\); variável dependente \(y = \tt{kid\_score}\) e o erro do modelo \(\sigma = \tt{sigma}\). A fórmula do modelo para o rstnarm é kid_score ~ mom_hs + mom_iq.

# Detectar quantos cores/processadores
options(mc.cores = parallel::detectCores())
options(Ncpus = parallel::detectCores())

library(rstanarm)
model <- stan_glm(
  kid_score ~ mom_hs + mom_iq,
  data = kidiq
)

Métricas da simulação MCMC

Um modelo estimado pelo rstanarm pode ser inspecionado em relação ao desempenho da amostragem MCMC. Ao chamarmos a função summary() no modelo estimado há uma parte chamada MCMC diagnostics.

summary(model)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs + mom_iq
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 434
 predictors:   3

Estimates:
              mean   sd   10%   50%   90%
(Intercept) 25.7    5.9 18.2  25.7  33.3 
mom_hs       6.0    2.2  3.1   6.0   8.9 
mom_iq       0.6    0.1  0.5   0.6   0.6 
sigma       18.2    0.6 17.4  18.2  19.0 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 86.8    1.2 85.2  86.8  88.4 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.1  1.0  5120 
mom_hs        0.0  1.0  4168 
mom_iq        0.0  1.0  4811 
sigma         0.0  1.0  4747 
mean_PPD      0.0  1.0  4306 
log-posterior 0.0  1.0  1778 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

A seção MCMC diagnostics possui três colunas de valores para cada parâmetro estimado do modelo.

No nosso caso, temos três parâmetros importantes:

1. valor do coeficiente da variável mom_hs;
2. valor do coeficiente da variável mom_iq; e
3. valor do erro residual do modelo linear sigma. As três métricas são:

• mcse: Monte Carlo Standard Error, o erro de mensuração da amostragem Monte Carlo do parâmetro;
• n_eff: uma aproximação crua do número de amostras efetivas amostradas pelo MCMC estimada pelo valor de Rhat; e
• Rhat: uma métrica de convergência e estabilidade da corrente Markov.

A métrica mais importante para levarmos em consideração é a Rhat que é uma métrica que mensura se as correntes Markov são estáveis e convergiram para um valor durante o progresso total das simulações. Ela é basicamente a proporção de variação ao compararmos duas metades das correntes após o descarte dos warmups. Valor de 1 implica em convergência e estabilidade. Como padrão o Rhat deve ser menor que 1.01 para que a estimação Bayesiana seja válida (S. P. Brooks & Gelman, 1998; Gelman & Rubin, 1992).

O que fazer se não obtermos convergência?

Dependendo do modelo e dos dados é possível que HMC (mesmo com NUTS) não atinja convergência. Nesse caso, ao rodar o modelo rstanarm dará diversos avisos de divergências. Aqui vou restringir o amostrador HMC do rstanarm para apenas 200 iterações com warmup padrão de metade das iterações (100) com duas correntes em paralelo (chains). Portanto, teremos \(2 \cdot (200 - 100) = 200\) amostras de MCMC. Se atente as mensagens de erro.

bad_model <- stan_glm(
  kid_score ~ mom_hs + mom_iq,
  data = kidiq,
  chains = 2,
  iter = 200
  )

Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
http://mc-stan.org/misc/warnings.html#bulk-ess

Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
http://mc-stan.org/misc/warnings.html#tail-ess

Esta é uma vantagem dos pacotes do ecossistema do Stan (incluindo rstanarm e brms). Quando o amostrador MCMC mostra problemas ele falha de uma maneira bem escandalosa com diversos avisos. Nunca ignore esses avisos, eles estão lá para te ajudar e indicar que seu modelo possui problemas sérios que devem ser inspecionados e sanados.

E vemos que o Rhat dos parâmetros estimados do modelo estão bem acima do limiar de \(1.01\).

summary(bad_model)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs + mom_iq
 algorithm:    sampling
 sample:       200 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 434
 predictors:   3

Estimates:
              mean   sd   10%   50%   90%
(Intercept) 25.8    6.3 17.8  25.7  33.7 
mom_hs       5.9    2.2  3.0   5.8   8.8 
mom_iq       0.6    0.1  0.5   0.6   0.6 
sigma       18.3    0.6 17.5  18.2  19.1 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 86.9    1.3 85.2  86.9  88.2 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.4  1.0  245  
mom_hs        0.1  1.0  231  
mom_iq        0.0  1.0  234  
sigma         0.1  1.0  112  
mean_PPD      0.1  1.0   78  
log-posterior 0.2  1.0   59  

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Gráficos de Diagnósticos do MCMC

O pacote rstanarm e brms tem diversos gráficos interessantes de diagnósticos de convergência das simulações MCMC. Eu recomendo o fluxo de visualizações de modelos Bayesianos de Gabry, Simpson, Vehtari, Betancourt, & Gelman (2019).

Traceplot

A primeira coisa que devemos ver quando há mensagens de avisos sobre divergências ou valores indesejáveis de Rhat é inspecionar as correntes Markov para ver se elas estão estacionárias ou se divergiram durante a amostragem do MCMC. Fazemos isso com a função plot(stanreg, "trace"). Objetos stanreg são modelos oriundos do rstanarm. No nosso caso temos dois objetos stanreg: o model e o bad_model.

O traceplot é a sobreposição das amostragens MCMC das correntes para cada parâmetro estimado (eixo vertical). A ideia é que as correntes se misturam e que não haja nenhuma inclinação ao longo das iterações (eixo horizontal). Isso demonstra que elas convergiram para um certo valor do parâmetro e se mantiveram nessa região durante boa parte (ou toda) da(a) amostragem das correntes Markov.

Detalhe: o traceplot usa somente as iterações válidas, após a remoção das iterações de warmup.

Vejam na figura 20 o traceplot do modelo que as correntes Markov convergiram e ficaram estacionárias durante a amostragem do MCMC (afinal esse é o modelo model que designamos iter = 2.000 e chains = 4, ambos padrões do rstanarm e brms). O ideal é sempre esse padrão no qual as correntes não apresentam uma tendência específica, ou seja, elas ficam geralmente “planas” na horizontal e não há uma grande variação de valores no eixo vertical (valor dos parâmetros). Esse padrão é muito parecido com “taturana.”

plot(model, "trace")

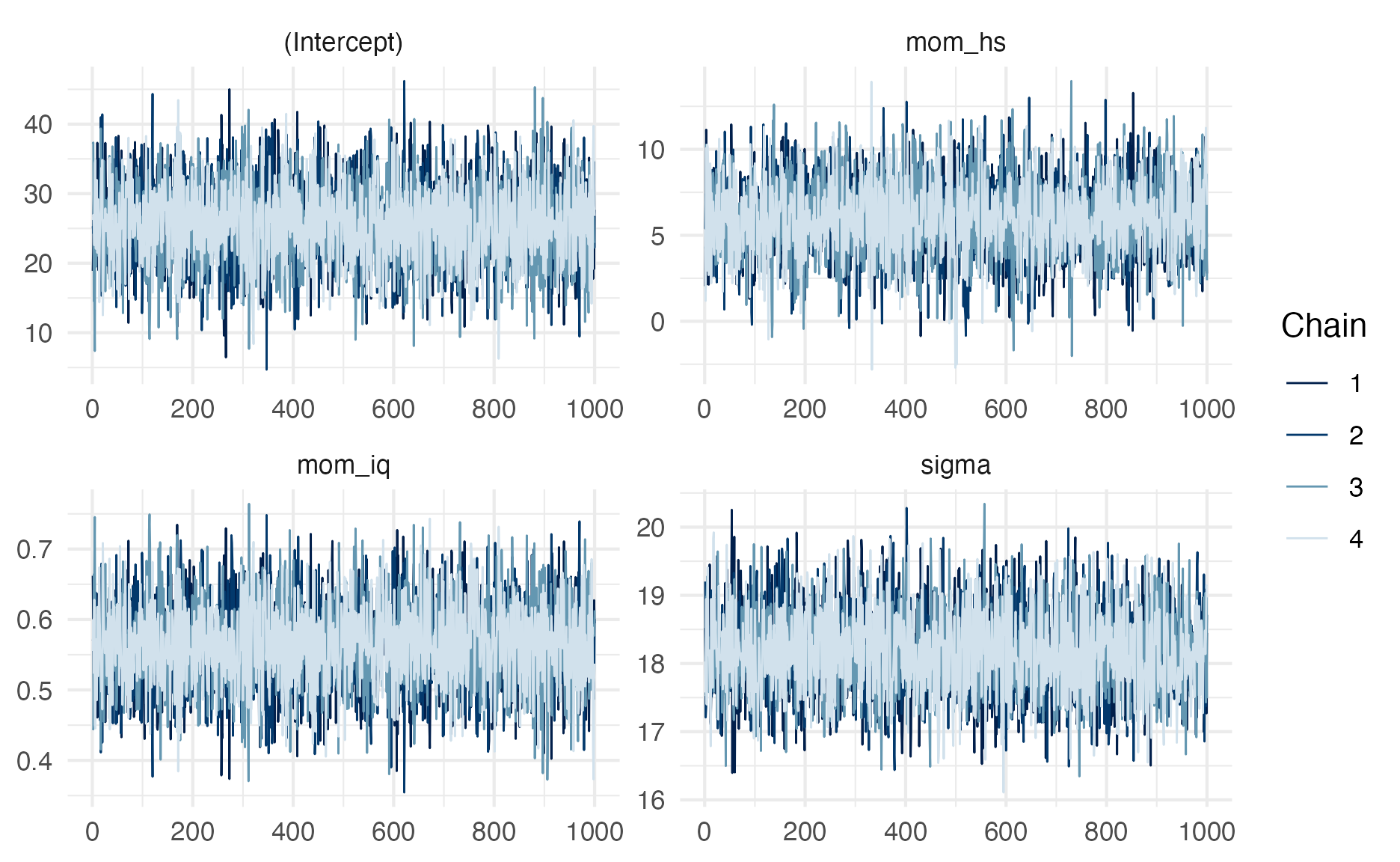
Figure 20: Traceplot do model

Na figura 21 temos o traceplot do modelo que as correntes Markov não convergiram, o bad_model (designamos iter = 200 e chains = 2). Aqui você vê que se aumentarmos o período de warmup e o número de iterações, provavelmente as correntes Markov convergiriam e ficariam estacionárias na região de maior probabilidade da posterior (e, consequentemente, dos parâmetros de interesse).

plot(bad_model, "trace")

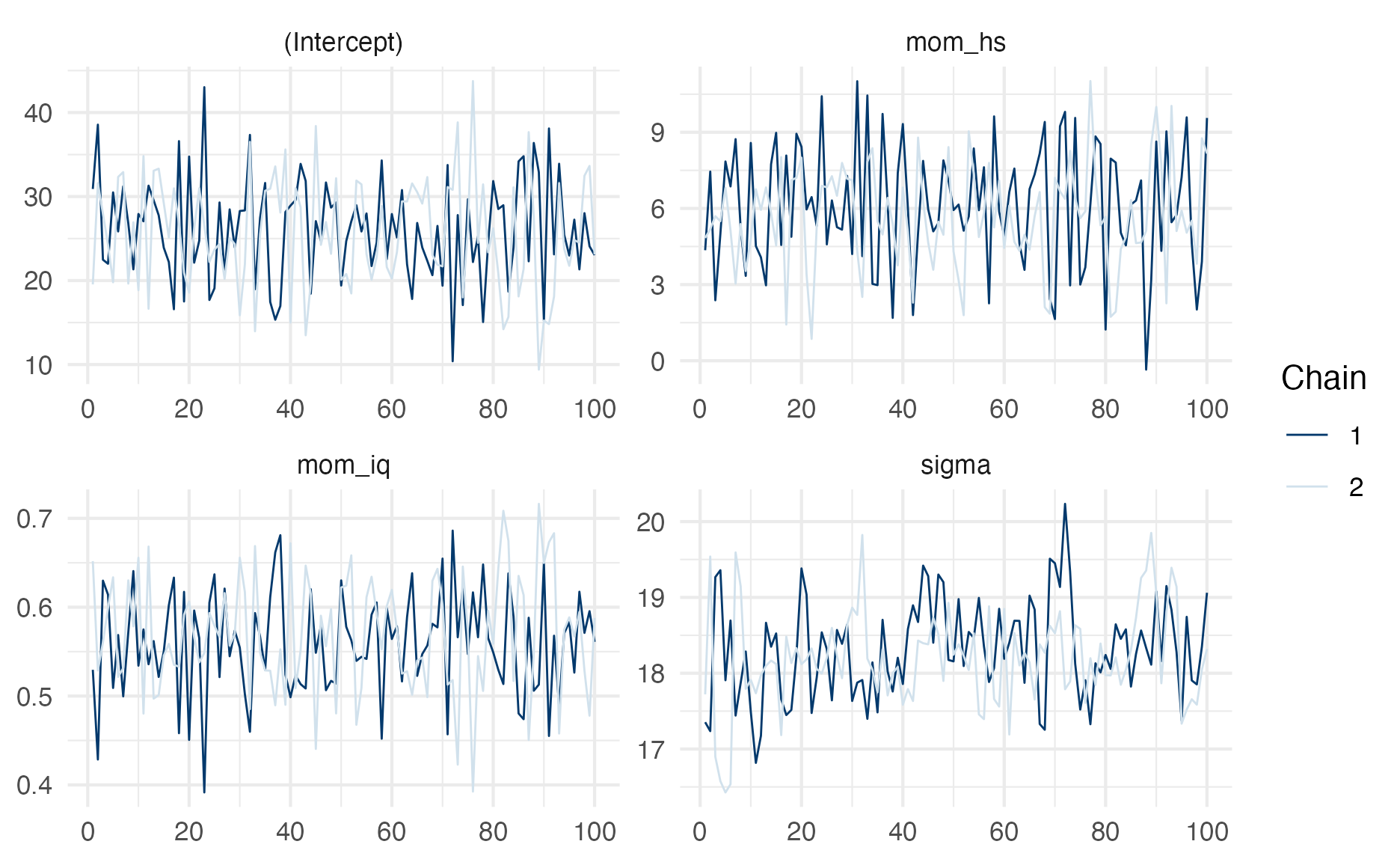
Figure 21: Traceplot do bad_model

Posterior Predictive Check

Um bom gráfico de diagnóstico é o posterior predictive check (PPC) que compara o histograma da variável dependente \(y\) contra o histograma de variáveis dependentes simuladas pelo modelo \(y_{\text{rep}}\) após a estimação dos parâmetros. A ideia é que os histogramas reais e simulados se misturem e não haja divergências. Fazemos isso com a função pp_check(stanreg).

Vejam na figura 22 o PPC do modelo que as correntes Markov convergiram e ficaram estacionárias durante a amostragem do MCMC (model). Podemos ver que as simulações \(y_{\text{rep}}\) realmente capturaram a natureza da variável dependente \(y\).

pp_check(model)

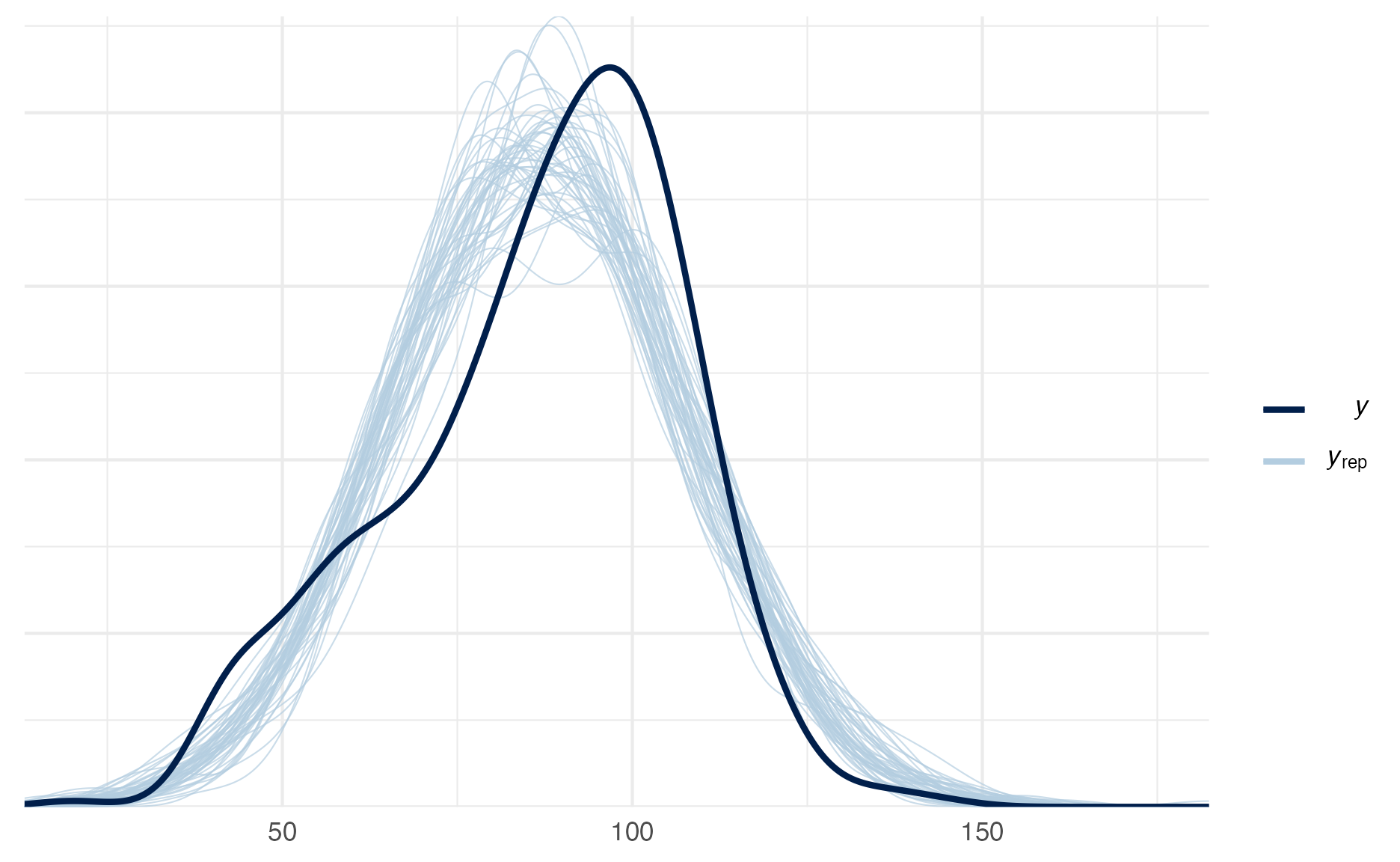
Figure 22: Posterior Preditive Check do model

Já na na figura 23 temos o PPC do modelo que as correntes Markov não convergiram, o bad_model. Aqui vemos que as simulações \(y_{\text{rep}}\) falharam em capturar a natureza da variável dependente \(y\). O PPC do bad_model também indica que se mantivéssemos um periodo maior de warmup e mais iterações das correntes Markov, provavelmente conseguiríamos ter um modelo que representasse muito bem o processo de geração de dados da nossa variável dependente \(y\).

pp_check(bad_model)

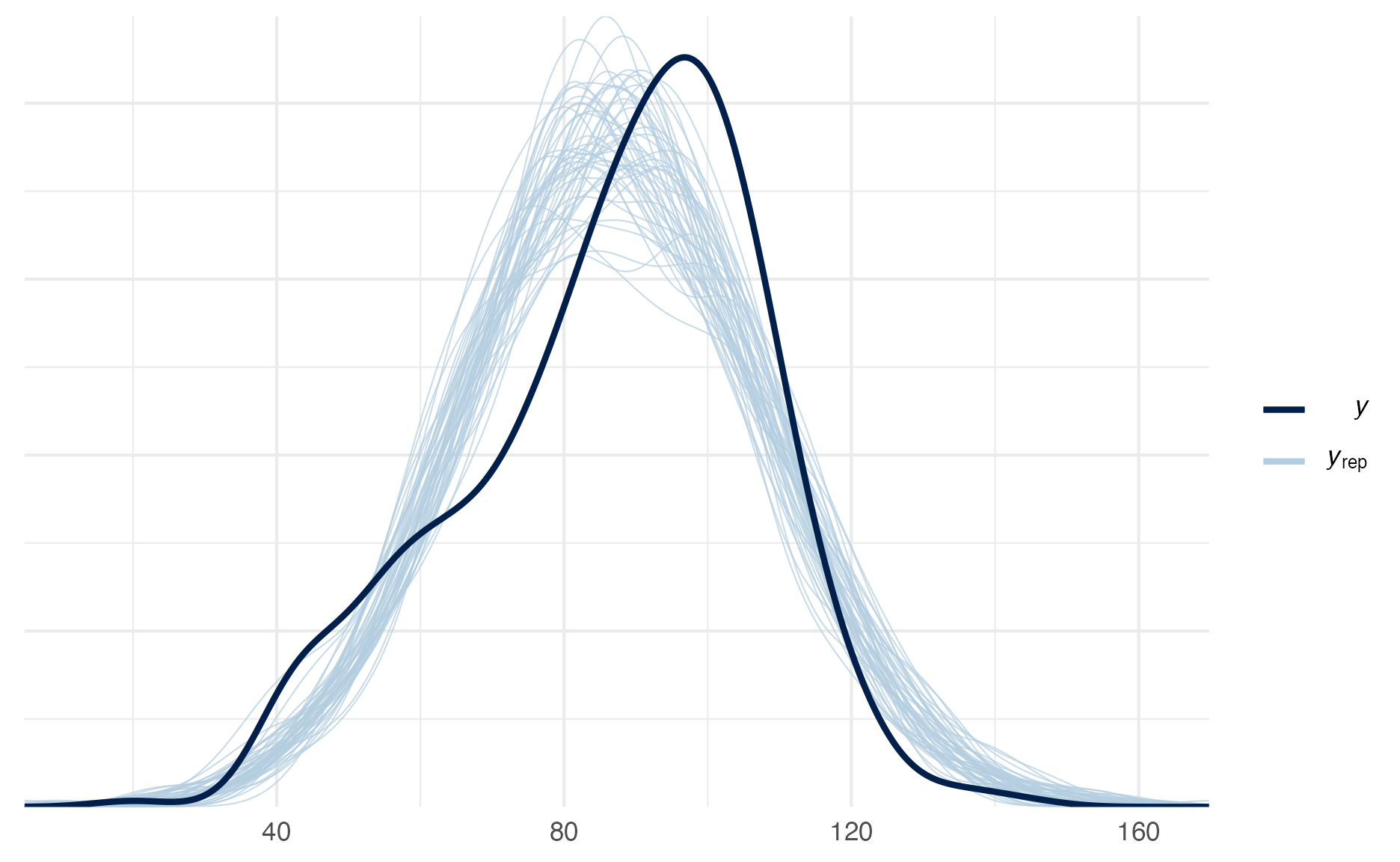
Figure 23: Posterior Preditive Check do bad_model

O quê fazer para convergir suas correntes Markov

Primeiro: Antes de fazer ajustes finos no número de correntes chains ou no número de iterações iter (entre outros …) saiba que o amostrador HMC-NUTS do Stan e seu ecossistema de pacotes (rstanarm e brms inclusos) é muito eficiente e eficaz em explorar as mais diversas complexas e “malucas” geometrias de distribuições-alvo posterior. Os argumentos padrões (iter = 2000, chains = 4 e warmup = floor(iter / 2)) funcionam perfeitamente para 99% dos casos (mesmo em modelos complexos). Dito isto, na maioria das vezes quando você possui problemas de amostragem e computacionais no seu modelo Bayesiano, o problema está na especificação do modelo e não no algoritmo de amostragem MCMC. Esta frase foi dita por Andrew Gelman (o “pai” do Stan) e é conhecido como o Folk Theorem (Gelman, 2008): “When you have computational problems, often there’s a problem with your model”.

Se o seu modelo Bayesiano está com problemas de convergência há alguns passos que podem ser tentados¹⁴. Aqui listados do mais simples para o mais complexo:

1. Aumentar o número de iterações e correntes: primeira opção é aumentar o número de iterações do MCMC com o argumento iter = XXX e também é possível aumentar o número de correntes com o argumento chains = X. Lembrando que o padrão é iter = 2000 e chains = 4.
2. Alterar a rotina de adaptação do HMC: a segunda opção é fazer com que o algoritmo de amostragem HMC fique mais conservador (com proposições de pulos menores). Isto pode ser alterado com o argumento adapt_delta da lista de opções control. control = list(adapt_delta = 0.9). O padrão do adapt_delta é control = list(adapt_delta = 0.8). Então qualquer valor entre \(0.8\) e \(1.0\) o torna mais conservador.
3. Reparametrização do Modelo: a terceira opção é reparametrizar o modelo. Há duas maneiras de parametrizar o modelo: a primeira com parametrização centrada (centered parameterization) e a segunda com parametrização não-centrada (non-centered parameterization). Não são assuntos que vamos cobrir aqui no curso. Recomendo o material de um dos desenvolvedores da linguagem Stan, Michael Betancourt.
4. Coletar mais dados: às vezes o modelo é complexo demais e precisamos de uma amostragem maior para conseguirmos estimativas estáveis.
5. Repensar o modelo: falha de convergência quando temos uma amostragem adequada geralmente é por conta de uma especificação de priors e verossimilhança que não são compatíveis com os dados. Nesse caso, é preciso repensar o processo generativo de dados no qual os pressupostos do modelo estão ancorados.

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] ggExtra_0.9          dplyr_1.0.6          rstan_2.21.2        
 [4] StanHeaders_2.21.0-7 MASS_7.3-54          ggforce_0.3.3       
 [7] gganimate_1.0.7      plotly_4.9.3         carData_3.0-4       
[10] DiagrammeR_1.0.6.1   brms_2.15.0          rstanarm_2.21.1     
[13] Rcpp_1.0.6           skimr_2.1.3          readr_1.4.0         
[16] readxl_1.3.1         tibble_3.1.2         ggplot2_3.3.3       
[19] patchwork_1.1.1      cowplot_1.1.1       

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         lazyeval_0.2.2       repr_1.1.3          
  [7] splines_4.1.0        crosstalk_1.1.1      rstantools_2.1.1    
 [10] inline_0.3.19        digest_0.6.27        htmltools_0.5.1.1   
 [13] magick_2.7.2         rsconnect_0.8.18     fansi_0.5.0         
 [16] magrittr_2.0.1       RcppParallel_5.1.4   matrixStats_0.59.0  
 [19] xts_0.12.1           prettyunits_1.1.1    colorspace_2.0-1    
 [22] textshaping_0.3.4    xfun_0.23            callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] polyclip_1.10-0      gtable_0.3.0         V8_3.4.2            
 [34] pkgbuild_1.2.0       abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] isoband_0.2.4        progress_1.2.2       viridisLite_0.4.0   
 [43] xtable_1.8-4         tmvnsim_1.0-2        stats4_4.1.0        
 [46] DT_0.18              httr_1.4.2           htmlwidgets_1.5.3   
 [49] threejs_0.3.3        RColorBrewer_1.1-2   ellipsis_0.3.2      
 [52] pkgconfig_2.0.3      loo_2.4.1            farver_2.1.0        
 [55] sass_0.4.0           here_1.0.1           utf8_1.2.1          
 [58] tidyselect_1.1.1     labeling_0.4.2       rlang_0.4.11        
 [61] reshape2_1.4.4       later_1.2.0          visNetwork_2.0.9    
 [64] munsell_0.5.0        cellranger_1.1.0     tools_4.1.0         
 [67] cli_2.5.0            generics_0.1.0       gifski_1.4.3-1      
 [70] ggridges_0.5.3       evaluate_0.14        stringr_1.4.0       
 [73] fastmap_1.1.0        yaml_2.2.1           ragg_1.1.2          
 [76] processx_3.5.2       knitr_1.33           purrr_0.3.4         
 [79] nlme_3.1-152         mime_0.10            projpred_2.0.2      
 [82] xml2_1.3.2           compiler_4.1.0       bayesplot_1.8.0     
 [85] shinythemes_1.2.0    rstudioapi_0.13      curl_4.3.1          
 [88] gamm4_0.2-6          png_0.1-7            tweenr_1.0.2        
 [91] bslib_0.2.5.1        stringi_1.6.2        highr_0.9           
 [94] ps_1.6.0             Brobdingnag_1.2-6    lattice_0.20-44     
 [97] Matrix_1.3-3         nloptr_1.2.2.2       markdown_1.1        
[100] shinyjs_2.0.0        vctrs_0.3.8          pillar_1.6.1        
[103] lifecycle_1.0.0      jquerylib_0.1.4      bridgesampling_1.1-2
[106] data.table_1.14.0    httpuv_1.6.1         R6_2.5.0            
[109] bookdown_0.22        promises_1.2.0.1     gridExtra_2.3       
[112] codetools_0.2-18     distill_1.2          boot_1.3-28         
[115] colourpicker_1.1.0   gtools_3.8.2         assertthat_0.2.1    
[118] rprojroot_2.0.2      withr_2.4.2          mnormt_2.0.2        
[121] shinystan_2.5.0      mgcv_1.8-35          parallel_4.1.0      
[124] hms_1.1.0            grid_4.1.0           tidyr_1.1.3         
[127] coda_0.19-4          minqa_1.2.4          rmarkdown_2.8       
[130] downlit_0.2.1        shiny_1.6.0          lubridate_1.7.10    
[133] base64enc_0.1-3      dygraphs_1.1.1.6    

---

1. o símbolo \(\propto\) (\propto) deve ser lido como “proporcional à.”↩︎

2. Algumas referências chamam esse processo de burnin.↩︎

3. Caso queira uma melhor explanação do algoritmo de Metropolis e Metropolis-Hastings sugiro ver Chib & Greenberg (1995)↩︎

4. do ingles probability density function (PDF).↩︎

5. objetos stanfit são objetos resultantes de modelos rstan ou rstanarm.↩︎

6. Caso queira uma melhor explanação do algoritmo de Gibbs sugiro ver Casella & George (1992).↩︎

7. isto ficará claro nas imagens e animações.↩︎

8. Vejam que aqui eu propositalmente dividi a neff por nrow(X_gibbs) / 2 (metade do número de iterações). Isso foi necessário, pois da maneira que eu codifiquei o algoritmo Gibbs ele amostra um parâmetro a cada interação e geralmente não se implementa um amostrador Gibbs dessa maneira (amostra-se todos os parâmetros por iteração). Eu fiz de propósito pois quero gerar nos GIFs animados na figura 10 a real trajetória do amostrador Gibbs no espaço amostral (vertical e horizontal, e não diagonal).↩︎

9. por questões de transbordamento numérico (numeric overflow) sempre trabalhamos com log de probabilidades.↩︎

10. 1.000 * 40 = 40.000. Esse 1 a mais é que usei a primeira iteração com Leapfrog \(L = 1\) como warmup.↩︎

11. NUTS é um algoritmo que usa o integrador simplético leapfrog e constrói uma árvore binária composta por nós de folha que são as simulações de dinâmicas Hamiltonianas usando \(2^j\) leapfrog steps nas direções para frente ou para trás no tempo no qual \(j\) é o número inteiro representando as iterações da construção da árvore binária. Uma vez que a particula simulada começa a retroceder sua trajetória a construção da árvore é interrompida e o numero ideal de \(L\) leapfrog steps é definido como \(2^j\) no tempo \(j-1\) do começo do retrocesso da trajetória. Então a partícula simulada nunca dá “meia-voltas” por isso No U-turn. Para mais detalhes sobre o algoritmo e como ele se relaciona com as dinâmicas Hamiltoninanas veja Hoffman & Gelman (2011).↩︎

12. além disso, todos os pacotes do ecossistema Stan aplicam uma decomposição QR na matriz \(X\) de dados, criando uma base ortogonal (não correlacionada) para amostragem. Isso faz com a distribuição-alvo (posterior) fique muito mais amigável do ponto de vista topológico/geométrico para o amostrador MCMC explorá-la de maneira mais eficiente e eficaz.↩︎

13. Sendo que, por padrão, Stan e rstanarm descartam a primeira metade (1.000) das iterações como aquecimento (warmup = floor(iter/2)).↩︎

14. além disso, vale a pena ativar a decomposição QR na matriz \(X\) de dados, criando uma base ortogonal (não correlacionada) para amostragem. Isso faz com a distribuição-alvo (posterior) fique muito mais amigável do ponto de vista topológico/geométrico para o amostrador MCMC explorá-la de maneira mais eficiente e eficaz. Só você especificar o argumento QR = TRUE dentro da funções do rstanarm, exemplo stan_glm(..., QR = TRUE). Ou, no brms você adicionar o argumento decomp = "QR" para qualquer fórmula dentro da função brm().↩︎