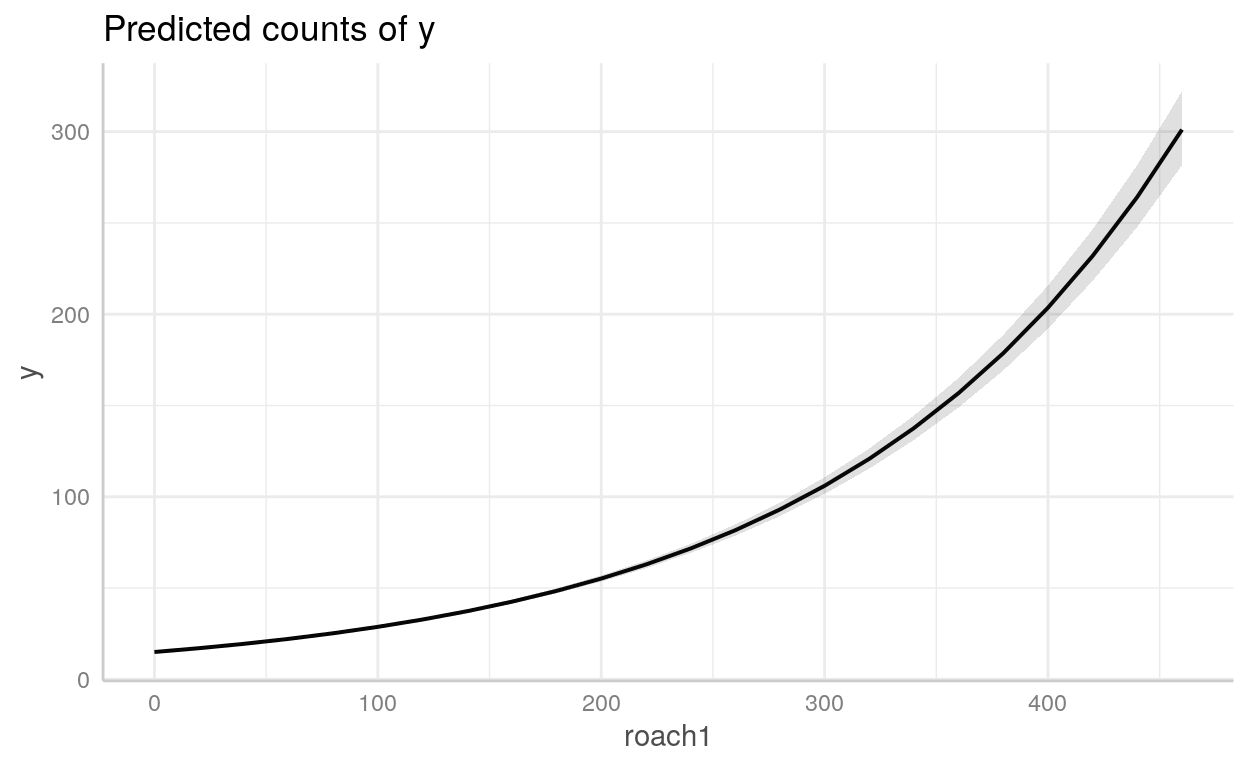Figure 1: Stats
Regressão Linear
Regressão linear permite com que você use uma ou mais variáveis discretas ou contínuas como variáveis independentes e mensurar o poder de associação com a variável dependente, que deve ser contínua.
Interpretações
Para compreender regressão linear podemos usar de três interpretações distintas mas complementares:
- Interpretação Geométrica: Regressão como uma reta.
- Interpretação Matemática: Regressão como otimização.
- Interpretação Estatística: Regressão como poder de associação entre variáveis controlando para diversos outros efeitos.
Interpretação Geométrica
Imagine que seus dados são pontos que vivem em um espaço multidimensional. A regressão é uma técnica para encontrar a melhor reta1 entre o conjunto de dados levando em conta todas as observações.
Isto é valido para qualquer espaço multidimensional, até para além de 3-D. Vamos mostrar um exemplo em 2-D da relação entre x e y, mas isto poder ser estendido para a relação x1, x2, … e y.
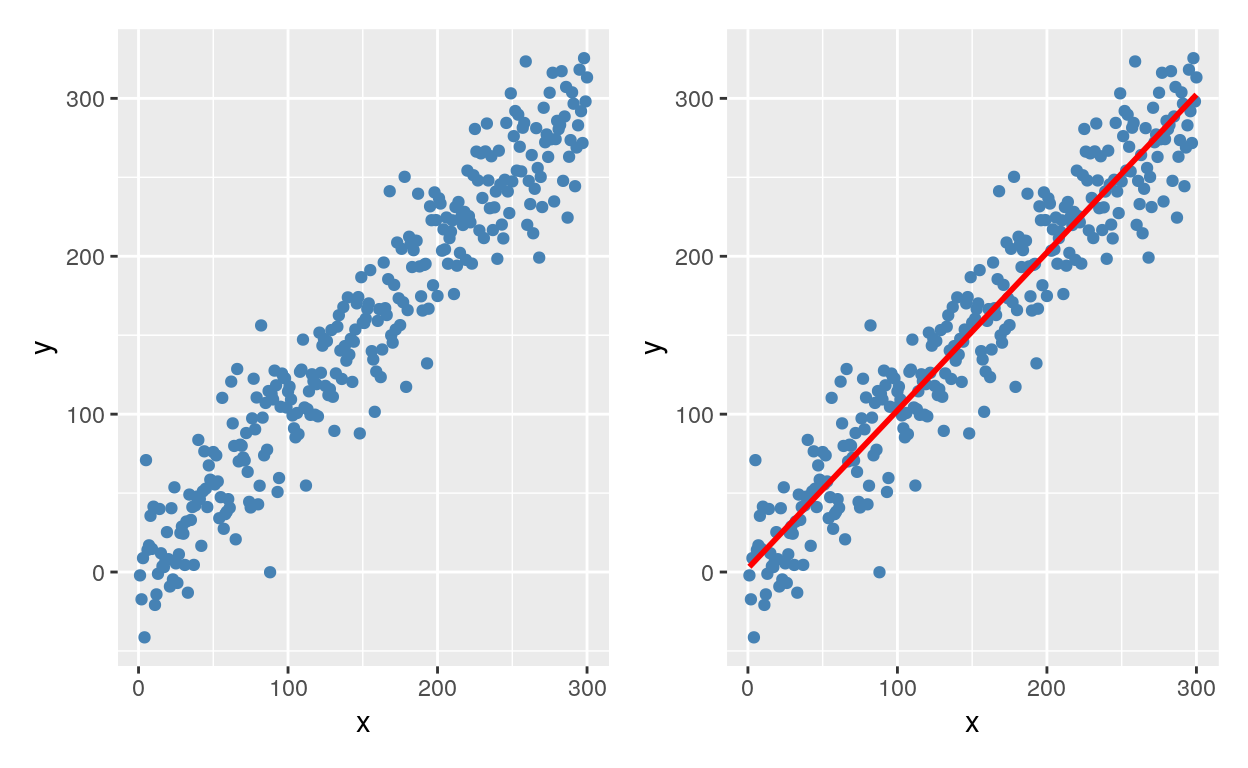
Figure 2: Uma relação entre variáveis representada por uma reta de tendência
Vejam que regressão linear usando apenas uma variável dependente e uma variável independente é a mesma coisa que que correlação.
Interpretação Matemática
A interpretação matemática é vista como uma otimização: encontrar a melhor reta entre os pontos que minimiza o erro quadrático médio (mean squared error – MSE). Ao escolhermos a melhor reta, devemos escolher a melhor reta que minimiza as distâncias entre os pontos, sendo que podemos errar para mais ou para menos. Para evitarmos que os erros se cancelem, precisamos eliminar o sinal negativo de alguns erros e convertê-los para valores positivos. Para isso, pegamos todas os erros (diferenças entre o valor previsto pela reta e o valor verdadeiro) e elevamos ao quadrado (assim todo número negativo se tornará positivo e todo positivo se manterá positivo). Portanto, a regressão se torna a busca do menor valor de uma função erro (MSE).
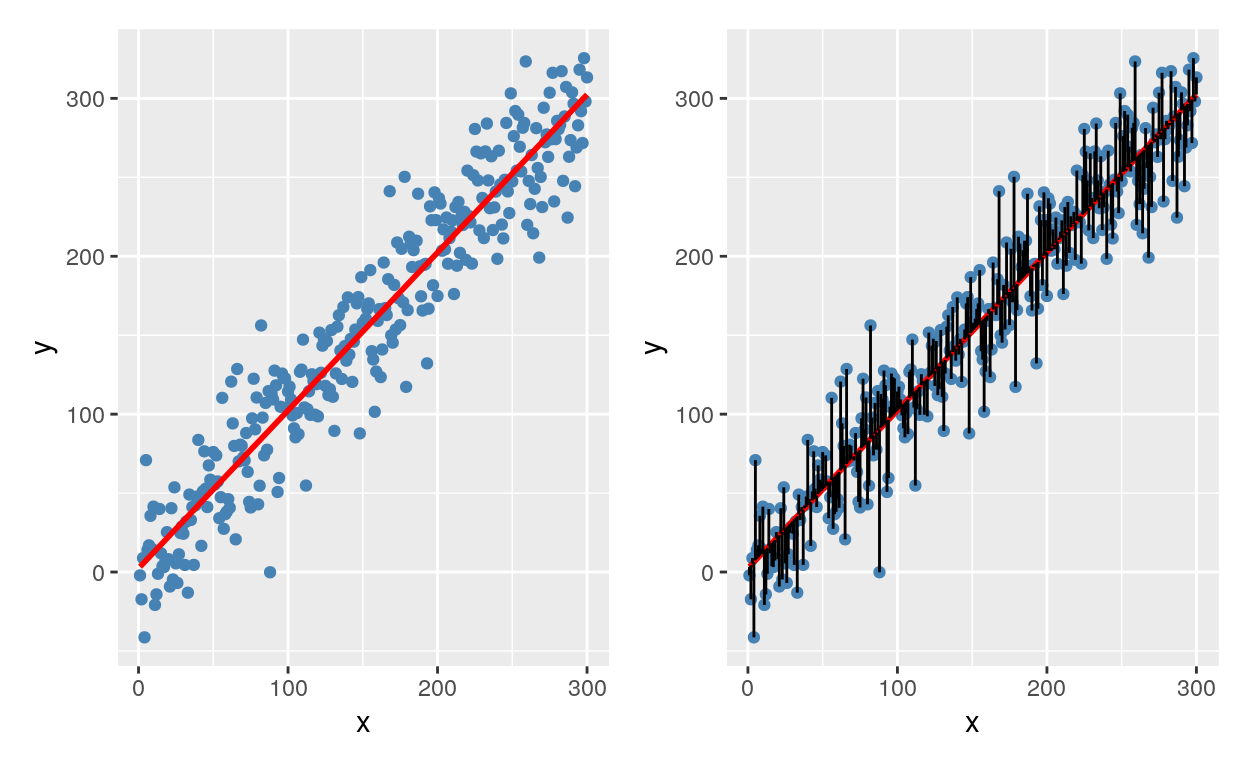
Figure 3: A melhor reta que minimiza a distância dos erros
Interpretação Estatística
A regressão linear usando uma única variável independente contínua se torna exatamente uma correlação. Agora quando empregamos mais de uma variável independente, a interpretação da regressão se torna: “O efeito de X em Y mantendo Z fixo”. Isto quer dizer que a regressão linear controla os efeitos das diferentes variáveis independentes ao calcular o efeito de uma certa variável independente. Esta é o que chamamos de interpretação estatística da regressão linear.
Por exemplo, digamos que você esteja em busca dos fatores que acarretam ataque cardíaco. Você coleta dados de pessoas que quantifiquem as seguintes variáveis: sono, stress, tabagismo, sedentarismo, entre outros… A regressão te permite mensurar o efeito de qualquer uma dessas variáveis na prevalência de ataque cardíaco controlando para outros efeitos. Em outras palavras, é possível mensurar o efeito de stress em ataque cardíaco, mantendo fixo os efeitos de sono, tabagismo, sedentarismo, etc… Isso permite você isolar o efeito de uma variável sem deixar que outras variáveis a influenciem na mensuração da sua relação com a variável dependente (no nosso caso: ataque cardíaco).
Exemplo - Score de QI de crianças
Para o nosso exemplo, usarei um dataset famoso chamado kidiq que está incluído no diretório datasets/. São dados de uma survey de mulheres adultas norte-americanas e seus respectivos filhos. Datado de 2007 possui 434 observações e 4 variáveis:
kid_score: QI da criançamom_hs: binária (0 ou 1) se a mãe possui diploma de ensino médiomom_iq: QI da mãemom_age: idade da mãe
Como especificar um modelo em R usando a sintaxe de “formula”
Podemos espeficiar modelos usando a sintaxe de formula:
y ~ x1 + x2 + ...
Call:
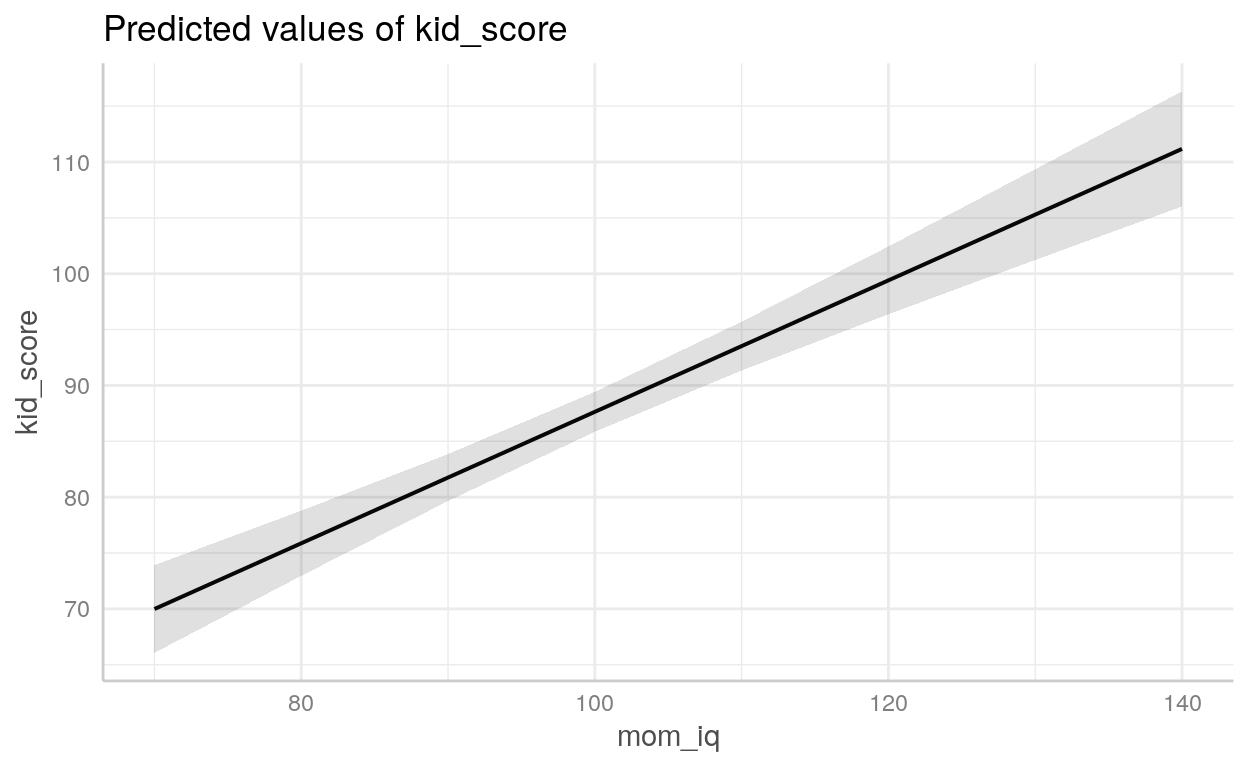
lm(formula = kid_score ~ mom_iq, data = kidiq)
Residuals:
Min 1Q Median 3Q Max
-56.75 -12.07 2.22 11.71 47.69
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 25.7998 5.9174 4.36 0.000016 ***
mom_iq 0.6100 0.0585 10.42 < 0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 18 on 432 degrees of freedom
Multiple R-squared: 0.201, Adjusted R-squared: 0.199
F-statistic: 109 on 1 and 432 DF, p-value: <0.0000000000000002
Call:
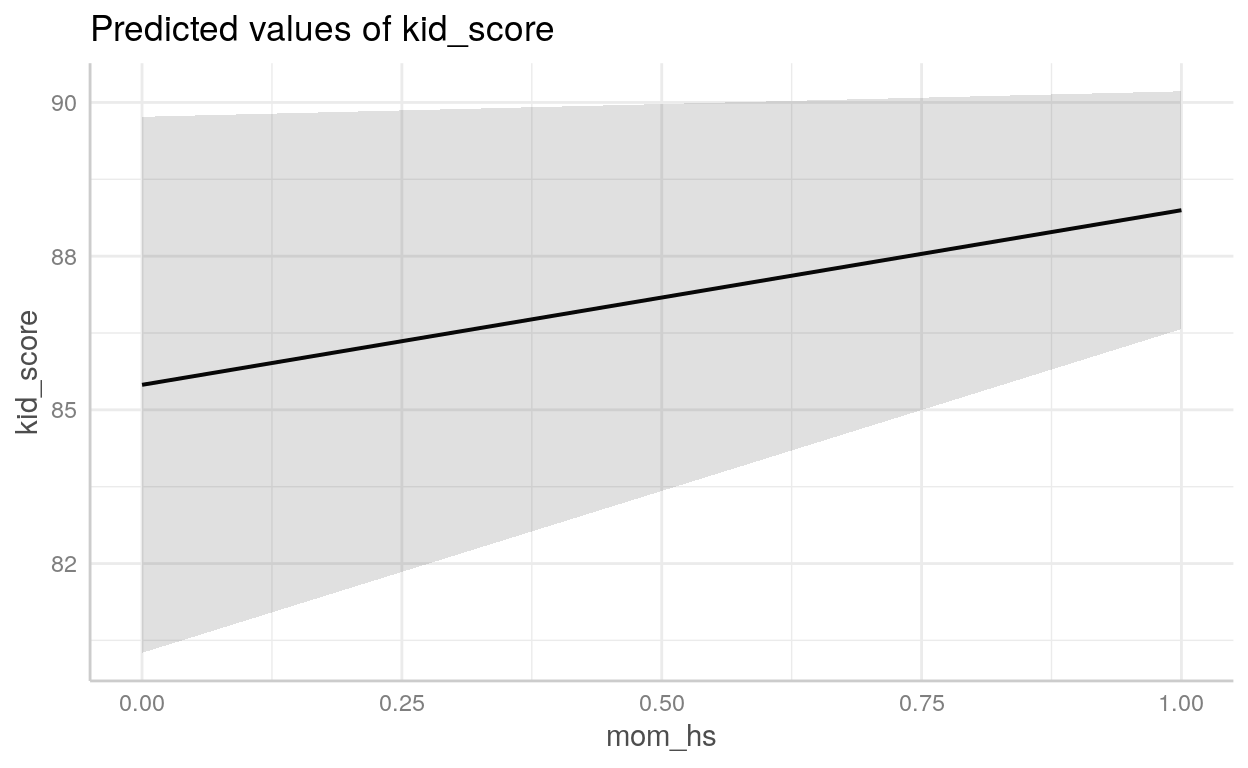
lm(formula = kid_score ~ mom_iq + mom_hs, data = kidiq)
Residuals:
Min 1Q Median 3Q Max
-52.9 -12.7 2.4 11.4 49.5
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 25.7315 5.8752 4.38 0.000015 ***
mom_iq 0.5639 0.0606 9.31 < 0.0000000000000002 ***
mom_hs 5.9501 2.2118 2.69 0.0074 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 18 on 431 degrees of freedom
Multiple R-squared: 0.214, Adjusted R-squared: 0.21
F-statistic: 58.7 on 2 and 431 DF, p-value: <0.0000000000000002
Call:
lm(formula = kid_score ~ mom_iq * mom_hs, data = kidiq)
Residuals:
Min 1Q Median 3Q Max
-52.09 -11.33 2.07 11.66 43.88
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -11.482 13.758 -0.83 0.4044
mom_iq 0.969 0.148 6.53 0.00000000018 ***
mom_hs 51.268 15.338 3.34 0.0009 ***
mom_iq:mom_hs -0.484 0.162 -2.99 0.0030 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 18 on 430 degrees of freedom
Multiple R-squared: 0.23, Adjusted R-squared: 0.225
F-statistic: 42.8 on 3 and 430 DF, p-value: <0.0000000000000002Se você quiser plotar modelos de regressão há o pacote {ggeffect}.
Regressão Logística
Uma regressão logística se comporta exatamente como um modelo linear: faz uma predição simplesmente computando uma soma ponderada das variáveis independentes, mais uma constante. Porém ao invés de retornar um valor contínuo, como a regressão linear, retorna a função logística desse valor.
\[\operatorname{Logística}(x) = \frac{1}{1 + e^{(-x)}}\]
A função logística é uma gambiarra transformação que pega qualquer valor entre menos infinito \(-\infty\) e mais infinito \(+\infty\) e transforma em um valor entre 0 e 1. Veja na figura 4 uma representação gráfica da função logística.
library(dplyr)
library(ggplot2)
tibble(
x = seq(-10, 10, length.out = 100),
logit = 1 / (1 + exp(-x))) %>%
ggplot(aes(x, logit)) +
geom_line()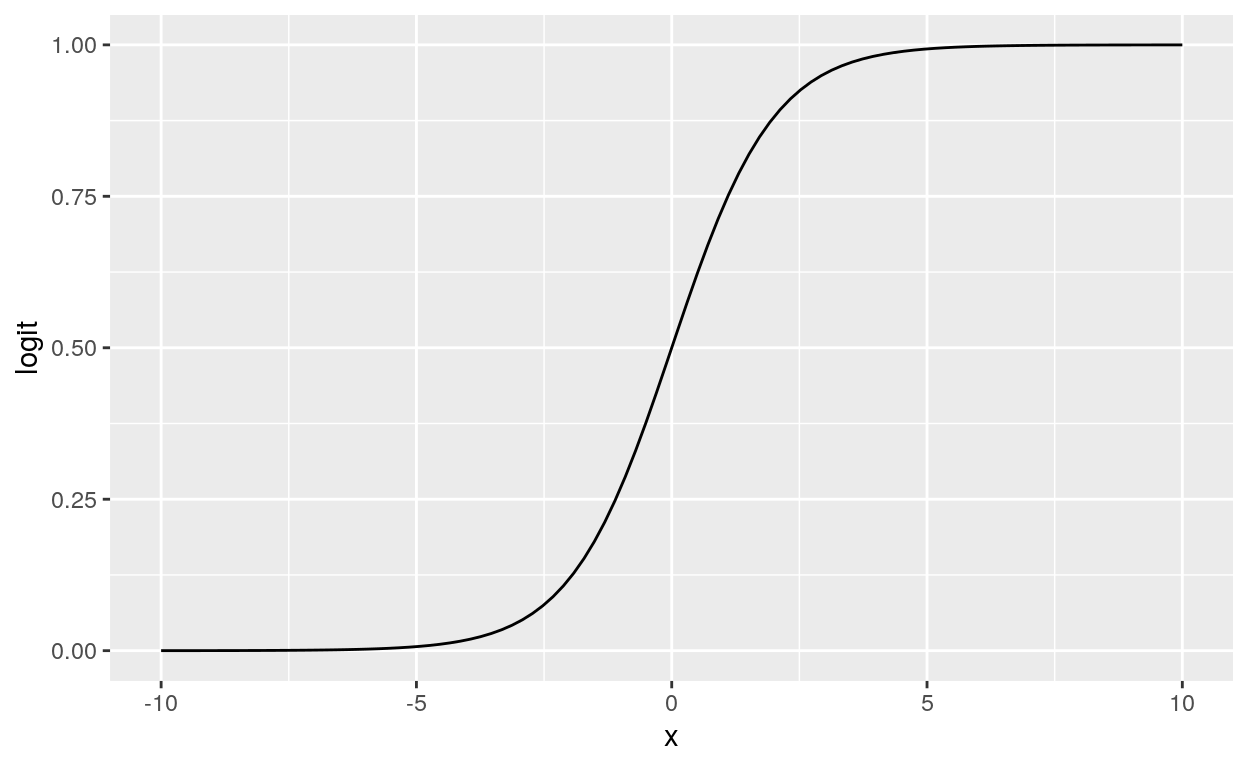
Figure 4: Função Logística
Ou seja, a função logística é a candidata ideal para quando precisamos converter algo contínuo sem restrições para algo contínuo restrito entre 0 e 1. Por isso ela é usada quando precisamos que um modelo tenha como variável dependente uma probabilidade (lembrando que qualquer numero real entre 0 e 1 é uma probabilidade válida). No caso de uma variável dependente binária, podemos usar essa probabilidade como a chance da variável dependente tomar valor de 0 ou de 1.
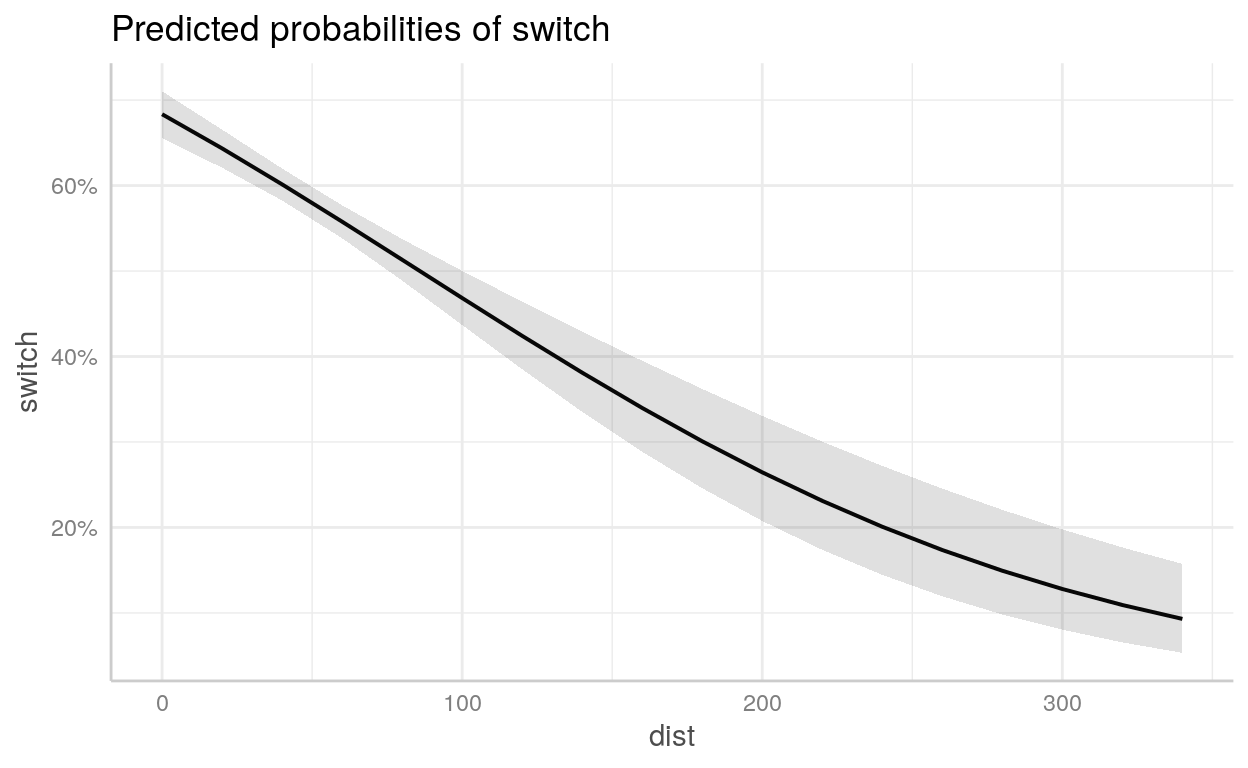
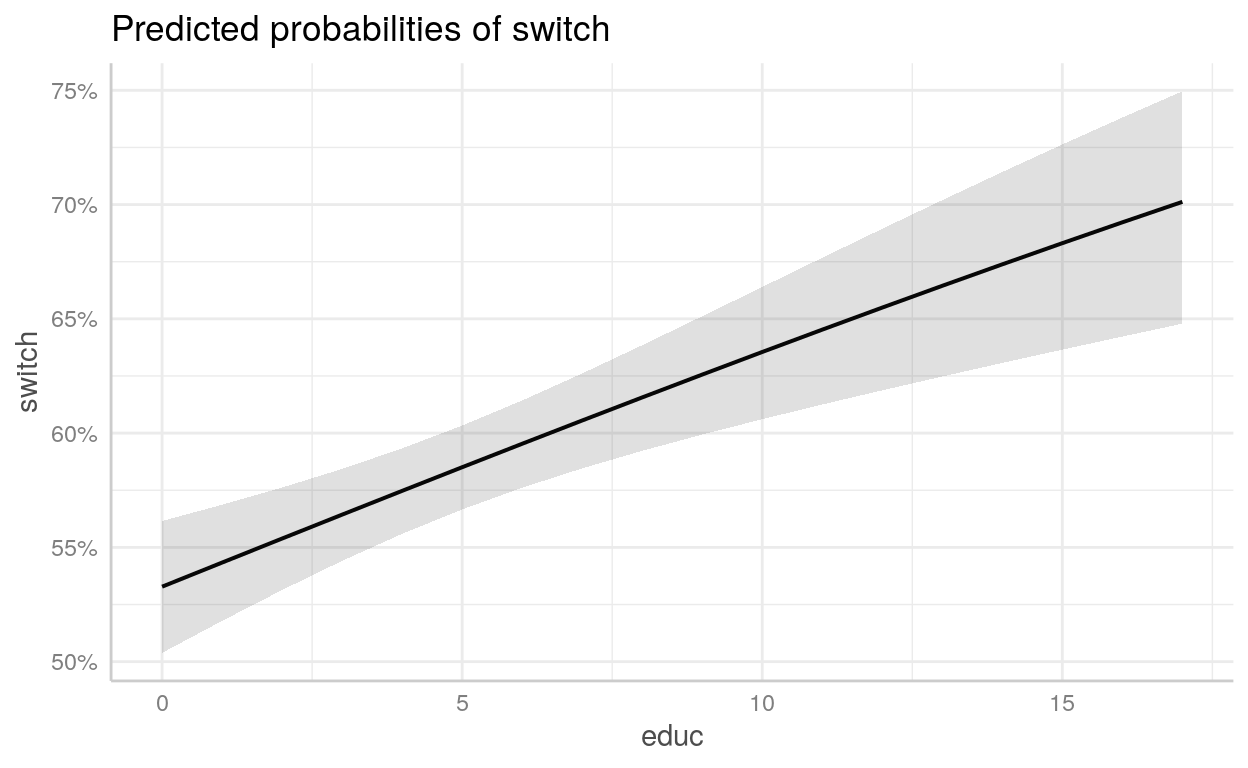
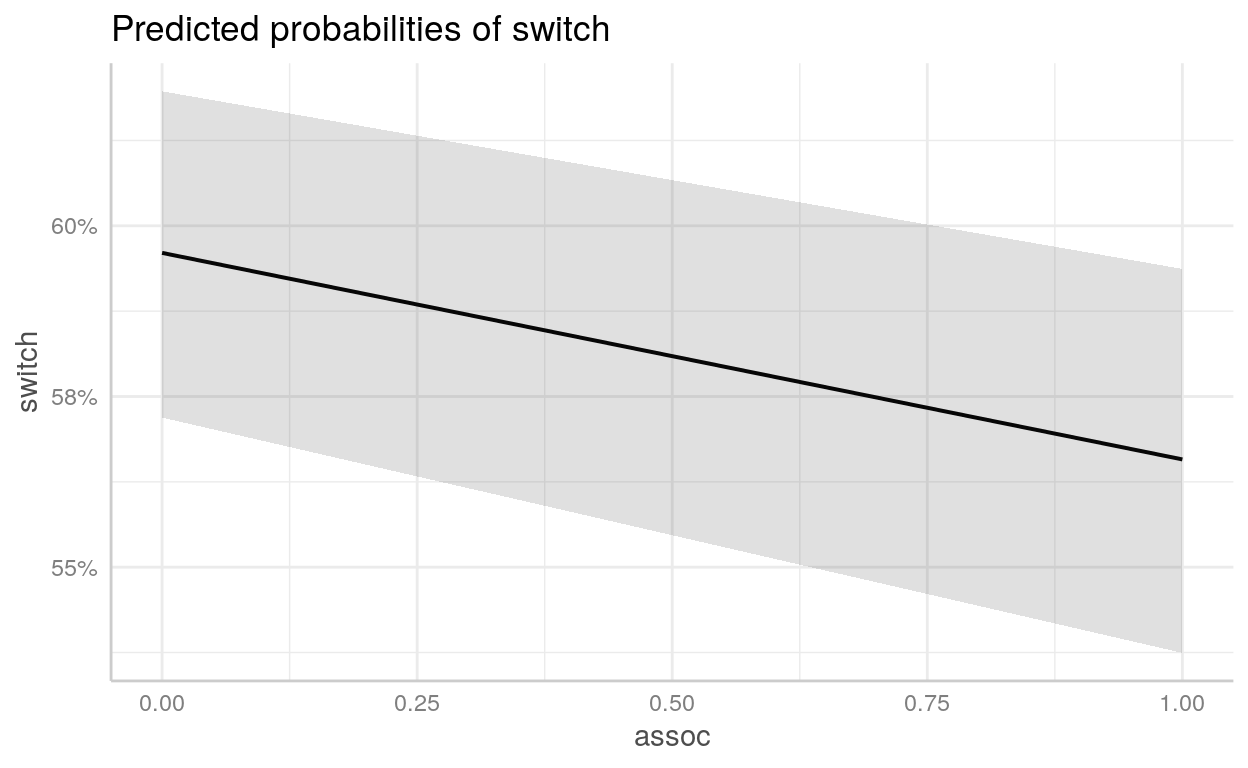
Exemplo - Propensão a mudar de poço de água contaminado
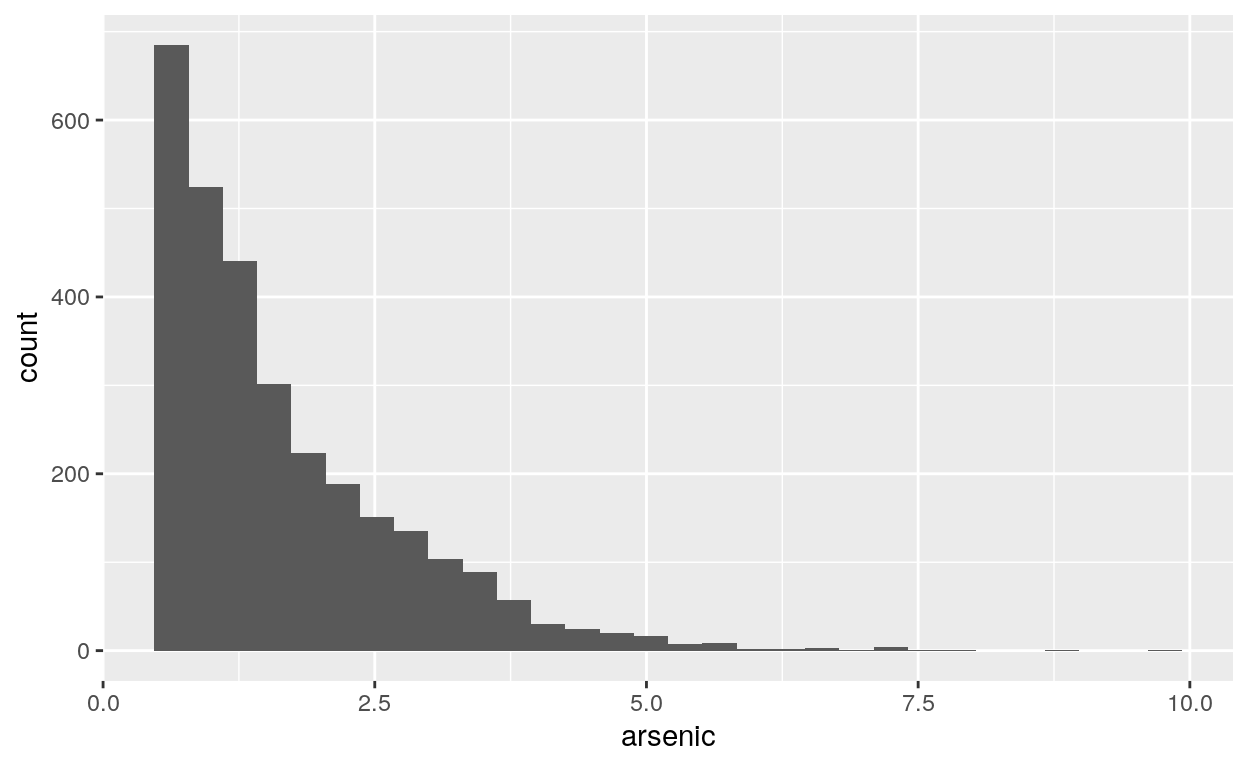
Para exemplo, usaremos um dataset chamado wells que está incluído no diretório datasets/. É uma survey com 3.200 residentes de uma pequena área de Bangladesh na qual os lençóis freáticos estão contaminados por arsênico. Respondentes com altos níveis de arsênico nos seus poços foram encorajados para trocar a sua fonte de água para uma níveis seguros de arsênico.
Possui as seguintes variáveis:
switch: dependente indicando se o respondente trocou ou não de poçoarsenic: nível de arsênico do poço do respondentedist: distância em metros da casa do respondente até o poço seguro mais próximoassociation: dummy se os membros da casa do respondente fazem parte de alguma organização da comunidadeeduc: quantidade de anos de educação que o chefe da família respondente possui
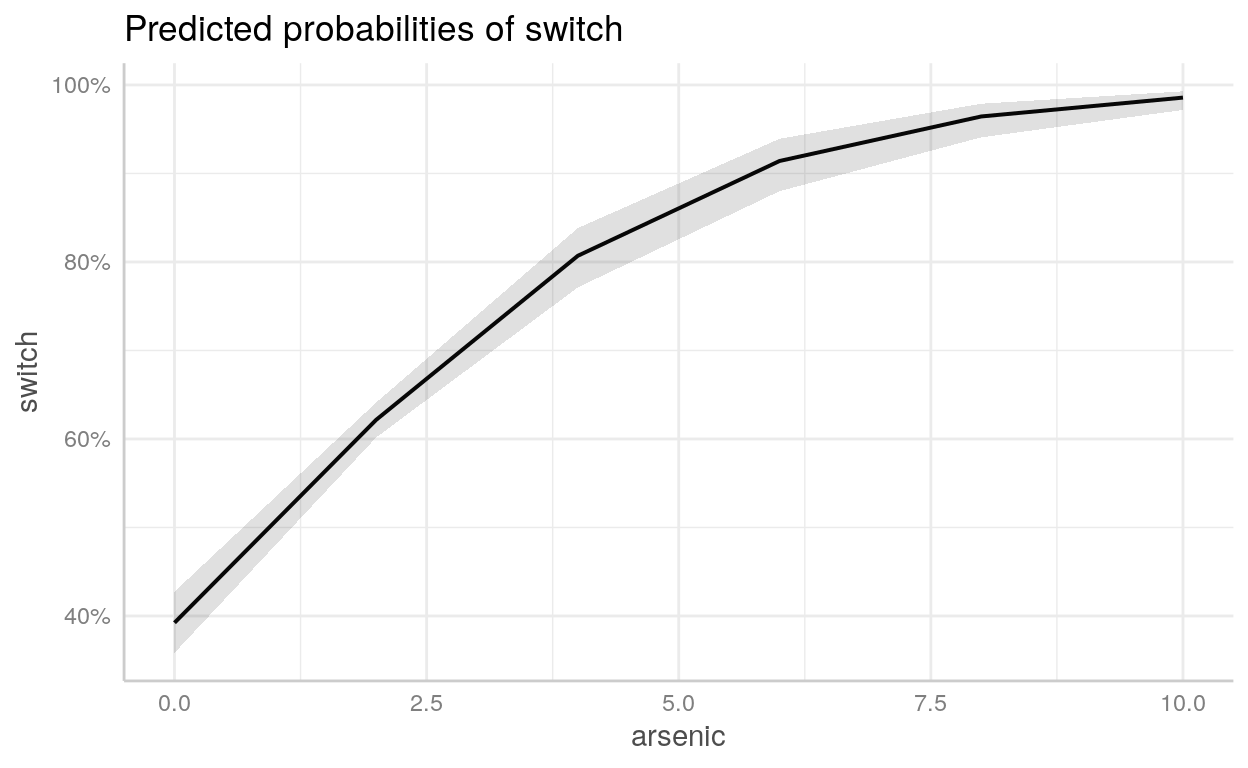
wells <- read_csv("datasets/wells.csv", col_types = "iddii")wells1 <- glm(switch ~ arsenic + dist + educ + assoc,
data = wells,
family = binomial)
summary(wells1)
Call:
glm(formula = switch ~ arsenic + dist + educ + assoc, family = binomial,
data = wells)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.594 -1.198 0.754 1.063 1.674
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.15671 0.09960 -1.57 0.12
arsenic 0.46702 0.04160 11.23 < 0.0000000000000002 ***
dist -0.00896 0.00105 -8.57 < 0.0000000000000002 ***
educ 0.04245 0.00959 4.43 0.0000095 ***
assoc -0.12430 0.07697 -1.61 0.11
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 4118.1 on 3019 degrees of freedom
Residual deviance: 3907.8 on 3015 degrees of freedom
AIC: 3918
Number of Fisher Scoring iterations: 4Vamos pegar o exp() dos coeficientes:
exp(wells1$coefficients)(Intercept) arsenic dist educ assoc
0.85 1.60 0.99 1.04 0.88 Regressão de Poisson - Dados de Contagem
Uma regressão de Poisson se comporta exatamente como um modelo linear: faz uma predição simplesmente computando uma soma ponderada das variáveis independentes \(\mathbf{X}\) pelos coeficientes estimados \(\boldsymbol{\beta}\), mais uma constante \(\alpha\). Porém ao invés de retornar um valor contínuo \(y\), como a regressão linear, retorna o logarítmo natural desse valor \(\log(y)\).
\[ \log(y)= \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_n x_n \]
que é o mesmo que
\[ y = e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_n x_n)} \]
- \(\theta\) - parâmetros do modelo
- \(\theta_0\) - constante
- \(\theta_1, \theta_2, \dots\) - coeficientes das variáveis independentes \(x_1, x_2, \dots\)
- \(n\) - número de variáveis independentes
A função \(e^x\) é chamada de função exponencial. Veja a figura 5 para uma intuição gráfica da função exponencial:
ggplot(data = tibble(
x = seq(0, 10, length.out = 100),
y = exp(x)
),
aes(x, y)) +
geom_line(size = 2, color = "steelblue") +
ylab("Exponencial(x)")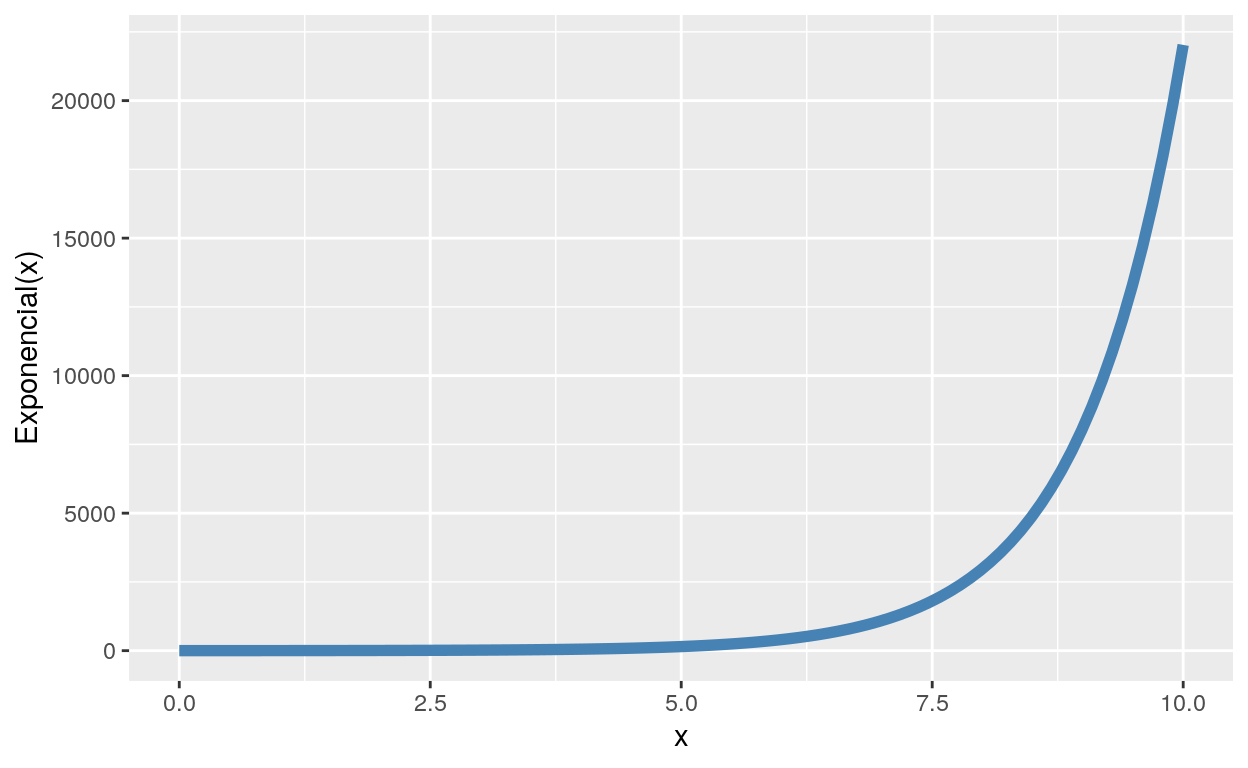
Figure 5: Função Exponencial
Regressão de Poisson é usada quando a nossa variável dependente só pode tomar valores positivos, geralmente em contextos de dados de contagem.
Exemplo Poisson - Exterminação de baratas
Para exemplo, usaremos um dataset chamado roaches que está incluído no diretório datasets/. É uma base de dados com 262 observações sobre a eficácia de um sistema de controle de pragas em reduzir o número de baratas (roaches) em apartamentos urbanos.
Possui as seguintes variáveis:
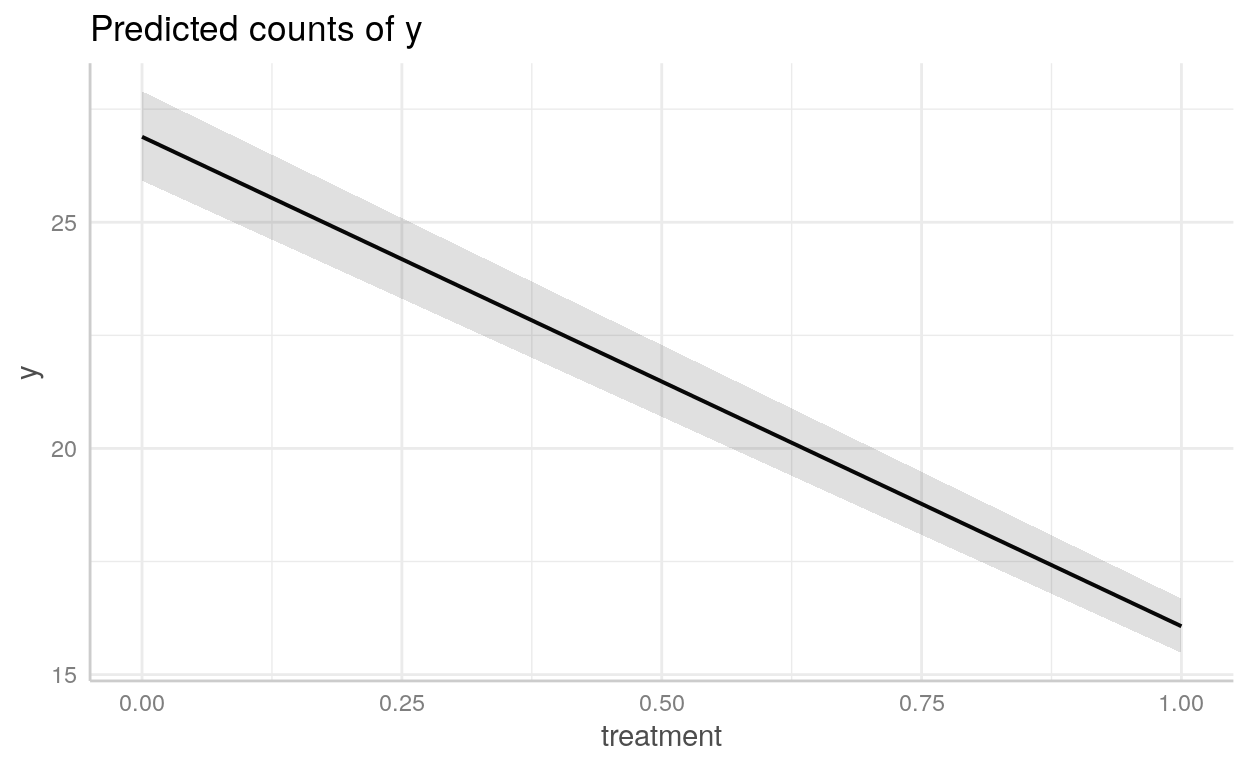
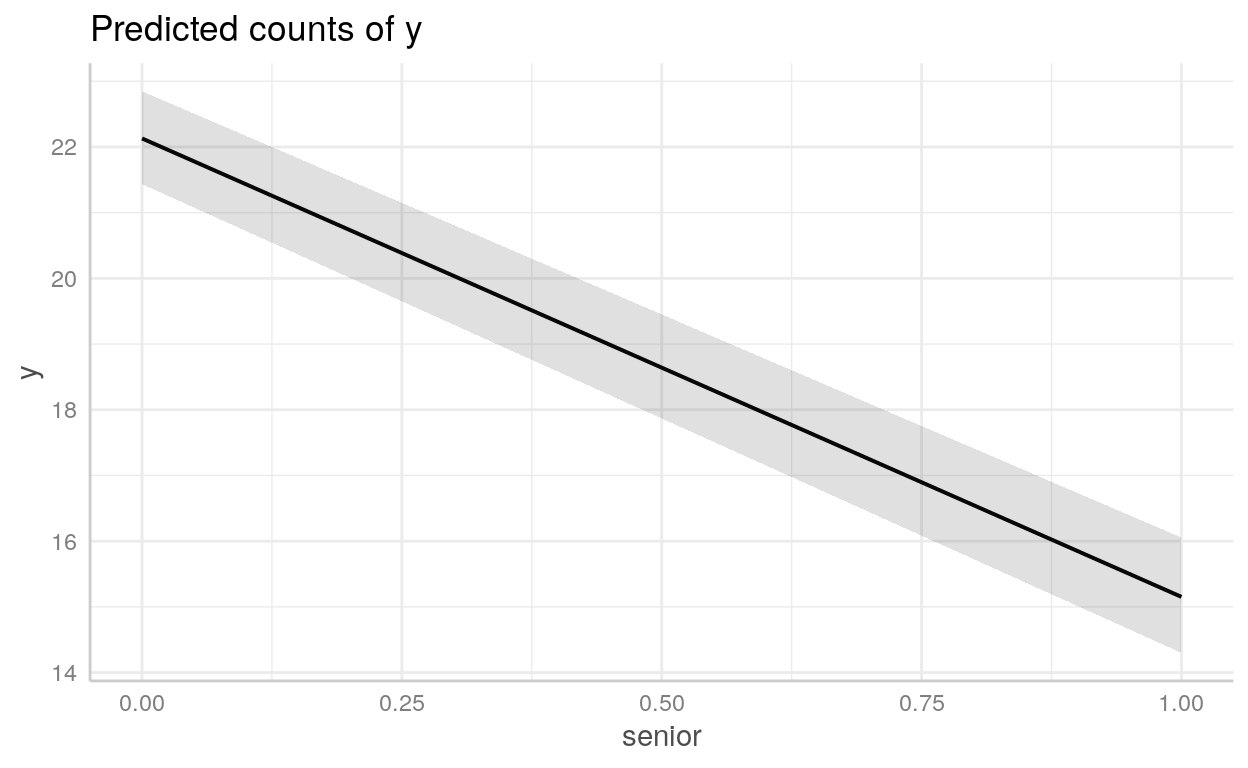
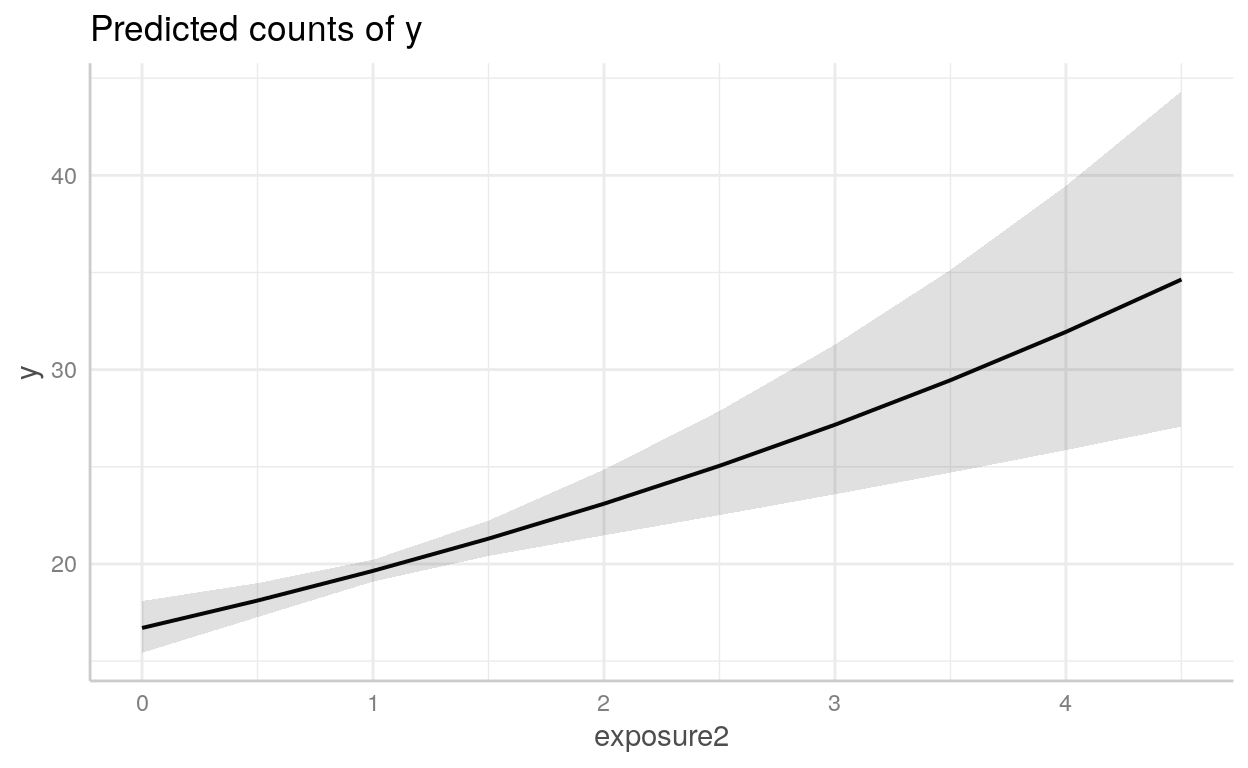
y: variável dependente - número de baratas mortasroach1: número de baratas antes da dedetizaçãotreatment: dummy para indicar se o apartamento foi dedetizado ou nãosenior: dummy para indicar se há apenas idosos no apartamentoexposure2: número de dias que as armadilhas de baratas foram usadas
roaches <- read_csv("datasets/roaches.csv", col_types = "idiid")roaches1 <- glm(
y ~ roach1 + treatment + senior + exposure2,
data = roaches,
family = poisson
)
summary(roaches1)
Call:
glm(formula = y ~ roach1 + treatment + senior + exposure2, family = poisson,
data = roaches)
Deviance Residuals:
Min 1Q Median 3Q Max
-18.35 -5.29 -4.18 0.29 27.67
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.9665993 0.0433859 68.38 < 0.0000000000000002 ***
roach1 0.0065252 0.0000902 72.38 < 0.0000000000000002 ***
treatment -0.5148722 0.0246802 -20.86 < 0.0000000000000002 ***
senior -0.3787607 0.0335552 -11.29 < 0.0000000000000002 ***
exposure2 0.1620458 0.0362256 4.47 0.0000077 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 16475 on 261 degrees of freedom
Residual deviance: 11431 on 257 degrees of freedom
AIC: 12195
Number of Fisher Scoring iterations: 6Vamos pegar o exp() dos coeficientes:
exp(roaches1$coefficients)(Intercept) roach1 treatment senior exposure2
19.43 1.01 0.60 0.68 1.18 Como plotar modelos com o {ggeffects}
Podemos usar o pacote [{ggeffects}](https://strengejacke.github.io/ggeffects/articles/practical_logisticmixedmodel.html) para *plotar* objetoslmeglm`
Ambiente
R version 4.2.2 (2022-10-31)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 22.04.1 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] ggeffects_1.1.5 broom_1.0.3 furrr_0.3.1
[4] future_1.31.0 purrr_1.0.1 ggridges_0.5.4
[7] ggExtra_0.10.0 gghighlight_0.4.0 ggrepel_0.9.3
[10] patchwork_1.1.2 forcats_1.0.0 plotly_4.10.1
[13] repurrrsive_1.1.0 ggplot2_3.4.1 stringr_1.5.0
[16] tidyr_1.3.0 janitor_2.2.0 dplyr_1.1.0
[19] readr_2.1.4 magrittr_2.0.3 tibble_3.1.8
loaded via a namespace (and not attached):
[1] minqa_1.2.5 colorspace_2.1-0 ellipsis_0.3.2
[4] rprojroot_2.0.3 estimability_1.4.1 snakecase_0.11.0
[7] rstudioapi_0.14 listenv_0.9.0 farver_2.1.1
[10] bit64_4.0.5 fansi_1.0.4 lubridate_1.9.2
[13] codetools_0.2-18 splines_4.2.2 downlit_0.4.2
[16] cachem_1.0.6 knitr_1.42 effects_4.2-2
[19] jsonlite_1.8.4 nloptr_2.0.3 dbplyr_2.3.0
[22] png_0.1-8 shiny_1.7.4 compiler_4.2.2
[25] httr_1.4.4 backports_1.4.1 assertthat_0.2.1
[28] Matrix_1.5-1 fastmap_1.1.0 lazyeval_0.2.2
[31] survey_4.1-1 cli_3.6.0 later_1.3.0
[34] htmltools_0.5.4 tools_4.2.2 gtable_0.3.1
[37] glue_1.6.2 Rcpp_1.0.10 carData_3.0-5
[40] jquerylib_0.1.4 vctrs_0.5.2 nlme_3.1-160
[43] crosstalk_1.2.0 insight_0.19.0 xfun_0.37
[46] globals_0.16.2 lme4_1.1-31 timechange_0.2.0
[49] mime_0.12 miniUI_0.1.1.1 lifecycle_1.0.3
[52] MASS_7.3-58.1 scales_1.2.1 vroom_1.6.1
[55] hms_1.1.2 promises_1.2.0.1 parallel_4.2.2
[58] RColorBrewer_1.1-3 yaml_2.3.7 memoise_2.0.1
[61] sass_0.4.5 distill_1.5 stringi_1.7.12
[64] RSQLite_2.3.0 highr_0.10 boot_1.3-28
[67] rlang_1.0.6 pkgconfig_2.0.3 evaluate_0.20
[70] lattice_0.20-45 htmlwidgets_1.6.1 labeling_0.4.2
[73] bit_4.0.5 tidyselect_1.2.0 parallelly_1.34.0
[76] bookdown_0.32 R6_2.5.1 generics_0.1.3
[79] DBI_1.1.3 pillar_1.8.1 withr_2.5.0
[82] mgcv_1.8-41 survival_3.4-0 nnet_7.3-18
[85] crayon_1.5.2 utf8_1.2.3 tzdb_0.3.0
[88] rmarkdown_2.20 grid_4.2.2 data.table_1.14.8
[91] blob_1.2.3 digest_0.6.31 xtable_1.8-4
[94] httpuv_1.6.9 munsell_0.5.0 viridisLite_0.4.1
[97] bslib_0.4.2 mitools_2.4 tecnicamente reta aqui se refere um hiperplano que é subespaço de dimensão \(n-1\) de um espaço de dimensão \(n\). Por exemplo, uma reta é um hiperplano 1-D de uma plano 2-D; um plano 2-D é um hiperplano de um plano 3-D; e assim por diante…↩︎