When to use Multilevel Models?
Hyperpriors
Three Approaches to Multilevel Models
Example - Cheese Ratings
References

Multilevel Models (a.k.a. Hierarchical Models)

Bayesian hierarchical models (also called multilevel models) are a statistical model written at multiple levels (hierarchical form) that estimates the parameters of the posterior distribution using the Bayesian approach. The sub-models combine to form the hierarchical model, and Bayes' theorem is used to integrate them with the observed data and to account for all the uncertainty that is present. The result of this integration is the posterior distribution, also known as an updated probability estimate, as additional evidence of the likelihood function is integrated together with the prior distribution of the parameters.

Hierarchical modeling is used when information is available at several different levels of observation units. The hierarchical form of analysis and organization helps to understand multiparameter problems and also plays an important role in the development of computational strategies.

Hierarchical models are mathematical statements that involve several parameters, so that the estimates of some parameters depend significantly on the values of other parameters. The figure below shows a hierarchical model in which there is a $\phi$ hyperparameter that parameterizes the parameters $\theta_1, \theta_2, \dots, \theta_N$ that are finally used to infer the posterior density of some variable of interest $\mathbf{y} = y_1, y_2, \dots, y_N$ .

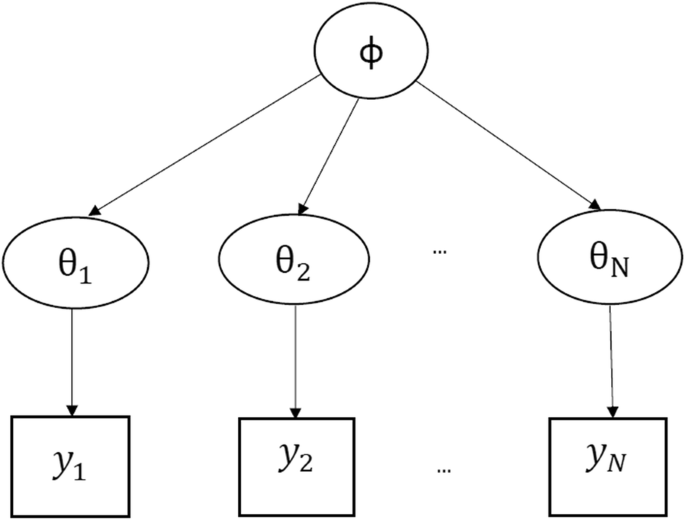
Bayesian Workflow

Hierarchical Model

When to use Multilevel Models?

Multilevel models are particularly suitable for research projects where participant data is organized at more than one level, i.e. nested data. Units of analysis are usually individuals (at a lower level) that are nested in contextual/aggregate units (at a higher level). An example is when we are measuring the performance of individuals and we have additional information about belonging to different groups such as sex, age group, hierarchical level, educational level or housing status.

There is a main assumption that cannot be violated in multilevel models which is exchangeability (de Finetti, 1974; Nau, 2001). Yes, this is the same assumption that we discussed in 2. What is Bayesian Statistics?. This assumption assumes that groups are exchangeable. The figure below shows a graphical representation of the exchangeability. The groups shown as "cups" that contain observations shown as "balls". If in the model's inferences, this assumption is violated, then multilevel models are not appropriate. This means that, since there is no theoretical justification to support exchangeability, the inferences of the multilevel model are not robust and the model can suffer from several pathologies and should not be used for any scientific or applied analysis.

Bayesian Workflow

Exchangeability – Images from Michael Betancourt

Hyperpriors

As the priors of the parameters are sampled from another prior of the hyperparameter (upper-level's parameter), which are called hyperpriors. This makes one group's estimates help the model to better estimate the other groups by providing more robust and stable estimates.

We call the global parameters as population effects (or population-level effects, also sometimes called fixed effects) and the parameters of each group as group effects (or group-level effects, also sometimes called random effects). That is why multilevel models are also known as mixed models in which we have both fixed effects and random effects.

Three Approaches to Multilevel Models

Multilevel models generally fall into three approaches:

Random-intercept model: each group receives a different intercept in addition to the global intercept.
Random-slope model: each group receives different coefficients for each (or a subset of) independent variable(s) in addition to a global intercept.
Random-intercept-slope model: each group receives both a different intercept and different coefficients for each independent variable in addition to a global intercept.
Correlated-Random-intercept-slope model: each group receives both a different intercept and different coefficients for each independent variable in addition to a global intercept; while also taking into account the correlation/covariance amongst intercept/coefficients.

Random-Intercept Model

The first approach is the random-intercept model in which we specify a different intercept for each group, in addition to the global intercept. These group-level intercepts are sampled from a hyperprior.

To illustrate a multilevel model, I will use the linear regression example with a Gaussian/normal likelihood function. Mathematically a Bayesian multilevel random-slope linear regression model is:

\begin{aligned} \mathbf{y} &\sim \text{Normal}\left( \alpha + \alpha_j + \mathbf{X} \cdot \boldsymbol{\beta}, \sigma \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \alpha_j &\sim \text{Normal}(0, \tau) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \\ \tau &\sim \text{Cauchy}^+(0, \psi_{\alpha})\\ \sigma &\sim \text{Exponential}(\lambda_\sigma) \end{aligned}

The priors on the global intercept $\alpha$ , global coefficients $\boldsymbol{\beta}$ and error $\sigma$ , along with the Gaussian/normal likelihood on $\mathbf{y}$ are the same as in the linear regression model. But now we have new parameters. The first are the group intercepts prior $\alpha_j$ that denotes that every group $1, 2, \dots, J$ has its own intercept sampled from a normal distribution centered on 0 with a standard deviation $\psi_\alpha$ . This group intercept is added to the linear predictor inside the Gaussian/normal likelihood function. The group intercepts' standard deviation $\tau$ have a hyperprior (being a prior of a prior) which is sampled from a positive-constrained Cauchy distribution (a special case of the Student- $t$ distribution with degrees of freedom $\nu = 1$ ) with mean 0 and standard deviation $\sigma_\alpha$ . This makes the group-level intercept's dispersions being sampled from the same parameter $\tau$ which allows the model to use information from one group intercept to infer robust information regarding another group's intercept dispersion and so on.

This is easily accomplished with Turing:

using Turing
using LinearAlgebra
using Statistics: mean, std
using Random: seed!
seed!(123)

@model function varying_intercept(
    X, idx, y; n_gr=length(unique(idx)), predictors=size(X, 2)
)
    #priors
    α ~ Normal(mean(y), 2.5 * std(y))       # population-level intercept
    β ~ filldist(Normal(0, 2), predictors)  # population-level coefficients
    σ ~ Exponential(std(y))                 # residual SD
    #prior for variance of random intercepts
    #usually requires thoughtful specification
    τ ~ truncated(Cauchy(0, 2); lower=0)    # group-level SDs intercepts
    αⱼ ~ filldist(Normal(0, τ), n_gr)       # group-level intercepts

    #likelihood
    ŷ = α .+ X * β .+ αⱼ[idx]
    return y ~ MvNormal(ŷ, σ^2 * I)
end;

Random-Slope Model

The second approach is the random-slope model in which we specify a different slope for each group, in addition to the global intercept. These group-level slopes are sampled from a hyperprior.

To illustrate a multilevel model, I will use the linear regression example with a Gaussian/normal likelihood function. Mathematically a Bayesian multilevel random-slope linear regression model is:

\begin{aligned} \mathbf{y} &\sim \text{Normal}\left( \alpha + \mathbf{X} \cdot \boldsymbol{\beta}_j \cdot \boldsymbol{\tau}, \sigma \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta}_j &\sim \text{Normal}(0, 1) \\ \boldsymbol{\tau} &\sim \text{Cauchy}^+(0, \psi_{\boldsymbol{\beta}})\\ \sigma &\sim \text{Exponential}(\lambda_\sigma) \end{aligned}

Here we have a similar situation from before with the same hyperprior, but now it is a hyperprior for the the group coefficients' standard deviation prior: $\boldsymbol{\beta}_j$ . This makes the group-level coefficients's dispersions being sampled from the same parameter $\tau$ which allows the model to use information from one group coefficients to infer robust information regarding another group's coefficients dispersion and so on.

In Turing we can accomplish this as:

@model function varying_slope(X, idx, y; n_gr=length(unique(idx)), predictors=size(X, 2))
    #priors
    α ~ Normal(mean(y), 2.5 * std(y))                    # population-level intercept
    σ ~ Exponential(std(y))                              # residual SD
    #prior for variance of random slopes
    #usually requires thoughtful specification
    τ ~ filldist(truncated(Cauchy(0, 2); lower=0), n_gr) # group-level slopes SDs
    βⱼ ~ filldist(Normal(0, 1), predictors, n_gr)        # group-level standard normal slopes

    #likelihood
    ŷ = α .+ X * βⱼ * τ
    return y ~ MvNormal(ŷ, σ^2 * I)
end;

Random-Intercept-Slope Model

The third approach is the random-intercept-slope model in which we specify a different intercept and slope for each group, in addition to the global intercept. These group-level intercepts and slopes are sampled from hyperpriors.

To illustrate a multilevel model, I will use the linear regression example with a Gaussian/normal likelihood function. Mathematically a Bayesian multilevel random-intercept-slope linear regression model is:

\begin{aligned} \mathbf{y} &\sim \text{Normal}\left( \alpha + \alpha_j + \mathbf{X} \cdot \boldsymbol{\beta}_j \cdot \boldsymbol{\tau}_{\boldsymbol{\beta}}, \sigma \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \alpha_j &\sim \text{Normal}(0, \tau_{\alpha}) \\ \boldsymbol{\beta}_j &\sim \text{Normal}(0, 1) \\ \tau_{\alpha} &\sim \text{Cauchy}^+(0, \psi_{\alpha})\\ \boldsymbol{\tau}_{\boldsymbol{\beta}} &\sim \text{Cauchy}^+(0, \psi_{\boldsymbol{\beta}})\\ \sigma &\sim \text{Exponential}(\lambda_\sigma) \end{aligned}

Here we have a similar situation from before with the same hyperpriors, but now we fused both random-intercept and random-slope together.

In Turing we can accomplish this as:

@model function varying_intercept_slope(
    X, idx, y; n_gr=length(unique(idx)), predictors=size(X, 2)
)
    #priors
    α ~ Normal(mean(y), 2.5 * std(y))                     # population-level intercept
    σ ~ Exponential(std(y))                               # residual SD
    #prior for variance of random intercepts and slopes
    #usually requires thoughtful specification
    τₐ ~ truncated(Cauchy(0, 2); lower=0)                 # group-level SDs intercepts
    τᵦ ~ filldist(truncated(Cauchy(0, 2); lower=0), n_gr) # group-level slopes SDs
    αⱼ ~ filldist(Normal(0, τₐ), n_gr)                    # group-level intercepts
    βⱼ ~ filldist(Normal(0, 1), predictors, n_gr)         # group-level standard normal slopes

    #likelihood
    ŷ = α .+ αⱼ[idx] .+ X * βⱼ * τᵦ
    return y ~ MvNormal(ŷ, σ^2 * I)
end;

In all of the models so far, we are using the MvNormal construction where we specify both a vector of means (first positional argument) and a covariance matrix (second positional argument). Regarding the covariance matrix σ^2 * I, it uses the model's errors σ, here parameterized as a standard deviation, squares it to produce a variance parameterization, and multiplies by I, which is Julia's LinearAlgebra standard module implementation to represent an identity matrix of any size.

Correlated-Random-Intercept-Slope Model

The third approach is the correlated-random-intercept-slope model in which we specify a different intercept and slope for each group, in addition to the global intercept. These group-level intercepts and slopes are sampled from hyperpriors. Finally, we also model the correlation/covariance amongst the intercepts and slopes. We assume that they are not independent anymore, rather they are correlated.

In order to model the correlation between parameters, we need a prior on correlation/covariance matrices. There are several ways to define priors on covariance matrices. In some ancient time, "Bayesian elders" used distributions such as the Wishart distribution and the Inverse Wishart distribution. However, priors on covariance matrices are not that intuitive, and can be hard to translate into real-world scenarios. That's why I much prefer to construct my covariances matrices from a correlation matrix and a vector of standard deviations. Remember that every covariance matrix $\boldsymbol{\Sigma}$ can be decomposed into:

\boldsymbol{\Sigma}=\text{diag}_\text{matrix}(\boldsymbol{\tau}) \cdot \boldsymbol{\Omega} \cdot \text{diag}_\text{matrix}(\boldsymbol{\tau})

where $\boldsymbol{\Omega}$ is a correlation matrix with $1$ s in the diagonal and the off-diagonal elements between -1 e 1 $\rho \in (-1, 1)$ . $\boldsymbol{\tau}$ is a vector composed of the variables' standard deviation from $\boldsymbol{\Sigma}$ (is is the $\boldsymbol{\Sigma}$ 's diagonal).

These are much more intuitive and easy to work with, specially if you are not working together with some "Bayesian elders". This approach leaves us with the need to specify a prior on correlation matrices. Luckily, we have the LKJ distribution: distribution for positive definite matrices with unit diagonals (exactly what a correlation matrix is).

To illustrate a multilevel model, I will use the linear regression example with a Gaussian/normal likelihood function. Mathematically a Bayesian multilevel correlated-random-intercept-slope linear regression model is:

\begin{aligned} \mathbf{y} & \sim \text{Normal}(\mathbf{X} \boldsymbol{\beta}_{j}, \sigma) \\ \boldsymbol{\beta}_j & \sim \text{Multivariate Normal}(\boldsymbol{\mu}_j, \boldsymbol{\Sigma}) \quad \text{for}\quad j \in \{ 1, \dots, J \} \\ \boldsymbol{\Sigma} & \sim \text{LKJ}(\eta) \\ \sigma & \sim \text{Exponential}(\lambda_\sigma) \end{aligned}

We don't have any $\alpha$ s. If we want a varying intercept, we just insert a column filled with $1$ s in the data matrix $\mathbf{X}$ . Mathematically, this makes the column behave like an "identity" variable (because the number $1$ in the multiplication operation $1 \cdot \beta$ is the identity element. It maps $x \to x$ keeping the value of $x$ intact) and, consequently, we can interpret the column's coefficient as the model's intercept.

In Turing we can accomplish this as:

using PDMats

@model function correlated_varying_intercept_slope(
    X, idx, y; n_gr=length(unique(idx)), predictors=size(X, 2)
)
    #priors
    Ω ~ LKJCholesky(predictors, 2.0) # Cholesky decomposition correlation matrix
    σ ~ Exponential(std(y))

    #prior for variance of random correlated intercepts and slopes
    #usually requires thoughtful specification
    τ ~ filldist(truncated(Cauchy(0, 2); lower=0), predictors) # group-level SDs
    γ ~ filldist(Normal(0, 5), predictors, n_gr)               # matrix of group coefficients

    #reconstruct Σ from Ω and τ
    Σ_L = Diagonal(τ) * Ω.L
    Σ = PDMat(Cholesky(Σ_L + 1e-6 * I))                        # numerical instability
    #reconstruct β from Σ and γ
    β = Σ * γ

    #likelihood
    return y ~ arraydist([Normal(X[i, :] ⋅ β[:, idx[i]], σ) for i in 1:length(y)])
end;

In the correlated_varying_intercept_slope model, we are using the efficient Cholesky decomposition version of the LKJ prior with LKJCholesky. We put priors on all group coefficients γ and reconstruct both the covariance matrix Σ and the coefficient matrix β.

Example - Cheese Ratings

For our example, I will use a famous dataset called cheese (Boatwright, McCulloch & Rossi, 1999), which is data from cheese ratings. A group of 10 rural and 10 urban raters rated 4 types of different cheeses (A, B, C and D) in two samples. So we have $4 \cdot 20 \cdot 2 = 160$ observations and 4 variables:

cheese: type of cheese from A to D
rater: id of the rater from 1 to 10
background: type of rater, either rural or urban
y: rating of the cheese

OK, let's read our data with CSV.jl and output into a DataFrame from DataFrames.jl:

using DataFrames
using CSV
using HTTP

url = "https://raw.githubusercontent.com/storopoli/Bayesian-Julia/master/datasets/cheese.csv"
cheese = CSV.read(HTTP.get(url).body, DataFrame)
describe(cheese)

4×7 DataFrame
 Row │ variable    mean     min    median  max    nmissing  eltype
     │ Symbol      Union…   Any    Union…  Any    Int64     DataType
─────┼───────────────────────────────────────────────────────────────
   1 │ cheese               A              D             0  String1
   2 │ rater       5.5      1      5.5     10            0  Int64
   3 │ background           rural          urban         0  String7
   4 │ y           70.8438  33     71.5    91            0  Int64

As you can see from the describe() output, the mean cheese ratings is around 70 ranging from 33 to 91.

In order to prepare the data for Turing, I will convert the Strings in variables cheese and background to Ints. Regarding cheese, I will create 4 dummy variables one for each cheese type; and background will be converted to integer data taking two values: one for each background type. My intent is to model background as a group both for intercept and coefficients. Take a look at how the data will look like for the first 5 observations:

for c in unique(cheese[:, :cheese])
    cheese[:, "cheese_$c"] = ifelse.(cheese[:, :cheese] .== c, 1, 0)
end

cheese[:, :background_int] = map(cheese[:, :background]) do b
    if b == "rural"
        1
    elseif b == "urban"
        2
    else
        missing
    end
end

first(cheese, 5)

5×9 DataFrame
 Row │ cheese   rater  background  y      cheese_A  cheese_B  cheese_C  cheese_D  background_int
     │ String1  Int64  String7     Int64  Int64     Int64     Int64     Int64     Int64
─────┼───────────────────────────────────────────────────────────────────────────────────────────
   1 │ A            1  rural          67         1         0         0         0               1
   2 │ A            1  rural          66         1         0         0         0               1
   3 │ B            1  rural          51         0         1         0         0               1
   4 │ B            1  rural          53         0         1         0         0               1
   5 │ C            1  rural          75         0         0         1         0               1

Now let's us instantiate our model with the data. Here, I will specify a vector of Ints named idx to represent the different observations' group memberships. This will be used by Turing when we index a parameter with the idx, e.g. αⱼ[idx].

X = Matrix(select(cheese, Between(:cheese_A, :cheese_D)));
y = cheese[:, :y];
idx = cheese[:, :background_int];

The first model is the varying_intercept:

model_intercept = varying_intercept(X, idx, y)
chain_intercept = sample(model_intercept, NUTS(), MCMCThreads(), 1_000, 4)
println(DataFrame(summarystats(chain_intercept)))

9×8 DataFrame
 Row │ parameters  mean       std       mcse        ess_bulk  ess_tail  rhat     ess_per_sec
     │ Symbol      Float64    Float64   Float64     Float64   Float64   Float64  Float64
─────┼───────────────────────────────────────────────────────────────────────────────────────
   1 │ α            70.7489   5.02573   0.176587     1049.21   944.855  1.00255      19.8948
   2 │ β[1]          2.91501  1.30963   0.0257346    2596.92  2763.9    1.00097      49.2419
   3 │ β[2]        -10.632    1.34056   0.028425     2224.99  2724.4    1.00189      42.1895
   4 │ β[3]          6.52144  1.3159    0.0265587    2450.36  2667.92   1.00052      46.463
   5 │ β[4]          1.09178  1.31719   0.0264376    2475.97  2627.54   1.00117      46.9485
   6 │ σ             7.3913   0.449209  0.00807096   3127.77  2530.83   1.00102      59.3078
   7 │ τ             6.11784  5.54993   0.152948     1863.81  1849.7    1.00172      35.341
   8 │ αⱼ[1]        -3.39662  4.92084   0.174051     1057.29   929.725  1.00312      20.0479
   9 │ αⱼ[2]         3.63474  4.95267   0.175295     1054.17   920.198  1.00331      19.9889

Here we can see that the model has a population-level intercept α along with population-level coefficients βs for each cheese dummy variable. But notice that we have also group-level intercepts for each of the groups αⱼs. Specifically, αⱼ[1] are the rural raters and αⱼ[2] are the urban raters.

Now let's go to the second model, varying_slope:

model_slope = varying_slope(X, idx, y)
chain_slope = sample(model_slope, NUTS(), MCMCThreads(), 1_000, 4)
println(DataFrame(summarystats(chain_slope)))

12×8 DataFrame
 Row │ parameters  mean        std       mcse       ess_bulk  ess_tail   rhat     ess_per_sec
     │ Symbol      Float64     Float64   Float64    Float64   Float64    Float64  Float64
─────┼────────────────────────────────────────────────────────────────────────────────────────
   1 │ α           71.6225     6.12929   0.80038     70.2758    24.8834  1.0542       1.3079
   2 │ σ            7.98871    0.435528  0.0142789  879.095   1907.61    1.00481     16.3607
   3 │ τ[1]         5.95148    5.05219   0.283585   297.117   1630.98    1.01456      5.52961
   4 │ τ[2]         7.13182    7.54656   1.22127    120.798     26.97    1.03962      2.24817
   5 │ βⱼ[1,1]      0.199936   0.839602  0.0512732  282.448    223.989   1.01652      5.25661
   6 │ βⱼ[2,1]     -0.933251   1.06721   0.0676919  231.737    252.835   1.01661      4.31283
   7 │ βⱼ[3,1]      0.522532   0.883634  0.035598   636.854   1246.34    1.02562     11.8524
   8 │ βⱼ[4,1]      0.0664401  0.797414  0.0514516  278.881    154.864   1.02163      5.19022
   9 │ βⱼ[1,2]      0.290895   0.843615  0.0732187  135.896     84.0176  1.03096      2.52915
  10 │ βⱼ[2,2]     -0.853134   1.05917   0.0568238  415.139    467.237   1.01995      7.7261
  11 │ βⱼ[3,2]      0.563184   0.876935  0.0375404  474.159    818.21    1.01366      8.82451
  12 │ βⱼ[4,2]      0.124051   0.787212  0.0525178  224.833    143.946   1.018        4.18434

Here we can see that the model has still a population-level intercept α. But now our population-level coefficients βs are replaced by group-level coefficients βⱼs along with their standard deviation τᵦs. Specifically βⱼ's first index denotes the 4 dummy cheese variables' and the second index are the group membership. So, for example βⱼ[1,1] is the coefficient for cheese_A and rural raters (group 1).

Now let's go to the third model, varying_intercept_slope:

model_intercept_slope = varying_intercept_slope(X, idx, y)
chain_intercept_slope = sample(model_intercept_slope, NUTS(), MCMCThreads(), 1_000, 4)
println(DataFrame(summarystats(chain_intercept_slope)))

15×8 DataFrame
 Row │ parameters  mean       std       mcse        ess_bulk  ess_tail  rhat     ess_per_sec
     │ Symbol      Float64    Float64   Float64     Float64   Float64   Float64  Float64
─────┼───────────────────────────────────────────────────────────────────────────────────────
   1 │ α           70.8973    7.06973   0.226273    1080.56    988.602  1.00354     13.1307
   2 │ σ            7.07716   0.403315  0.00763609  2791.06   2389.42   1.00236     33.9161
   3 │ τₐ           6.19068   5.86481   0.187349    1286.35   1007.7    1.00342     15.6313
   4 │ τᵦ[1]        6.19739   5.39243   0.202217     646.032  1159.5    1.00601      7.85039
   5 │ τᵦ[2]        6.24244   5.30258   0.215136     598.407  1527.72   1.00463      7.27167
   6 │ αⱼ[1]       -3.62952   5.05254   0.176822    1253.95    761.597  1.00336     15.2377
   7 │ αⱼ[2]        3.42934   5.05582   0.176181    1271.82    839.894  1.00348     15.4548
   8 │ βⱼ[1,1]      0.273658  0.779529  0.0188846   1727.94   1703.37   1.00193     20.9975
   9 │ βⱼ[2,1]     -0.88519   1.07495   0.0402493    794.926   375.533  1.00615      9.6597
  10 │ βⱼ[3,1]      0.540418  0.897065  0.0325307    849.719   418.537  1.00343     10.3255
  11 │ βⱼ[4,1]      0.119311  0.761924  0.0183527   1730.92   1000.11   1.00092     21.0336
  12 │ βⱼ[1,2]      0.230796  0.819673  0.0210441   1571.83   1681.27   1.00307     19.1004
  13 │ βⱼ[2,2]     -0.916136  1.02804   0.0319528   1027.79   2087.51   1.00208     12.4894
  14 │ βⱼ[3,2]      0.577911  0.873303  0.0269948   1094.9    1738.12   1.00304     13.3049
  15 │ βⱼ[4,2]      0.115502  0.784112  0.0186258   1758.58   1981.55   1.0031      21.3698

Now we have fused the previous model in one. We still have a population-level intercept α. But now we have in the same model group-level intercepts for each of the groups αⱼs and group-level along with their standard deviation τₐ. We also have the coefficients βⱼs with their standard deviation τᵦs. The parameters are interpreted exactly as the previous cases.

Now let's go to the fourth model, varying_intercept_slope. Here we are going to add a columns of into the data matrix X:

X_correlated = hcat(fill(1, size(X, 1)), X)
model_correlated = correlated_varying_intercept_slope(X_correlated, idx, y)
chain_correlated = sample(model_correlated, NUTS(), MCMCThreads(), 1_000, 4)
println(DataFrame(summarystats(chain_correlated)))

31×8 DataFrame
 Row │ parameters  mean         std        mcse          ess_bulk  ess_tail  rhat        ess_per_sec
     │ Symbol      Float64      Float64    Float64       Float64   Float64   Float64     Float64
─────┼───────────────────────────────────────────────────────────────────────────────────────────────
   1 │ Ω.L[1,1]     1.0         0.0        NaN             NaN      NaN      NaN          NaN
   2 │ Ω.L[2,1]     0.0499316   0.31051      0.00698543   1975.54  2314.64     1.00168      1.52283
   3 │ Ω.L[3,1]    -0.454537    0.249772     0.00571052   1977.49  2262.51     1.00096      1.52433
   4 │ Ω.L[4,1]     0.308835    0.25287      0.00599969   1843.28  2199.73     1.00014      1.42088
   5 │ Ω.L[5,1]    -0.125632    0.307712     0.00654629   2239.37  2376.57     1.00314      1.72619
   6 │ Ω.L[2,2]     0.946451    0.0731193    0.00168809   2176.21  2182.87     1.00018      1.67751
   7 │ Ω.L[3,2]     0.00316296  0.326756     0.00512707   4010.69  2567.33     1.0003       3.0916
   8 │ Ω.L[4,2]     0.0351896   0.354115     0.00527131   4546.36  3111.1      1.00178      3.50452
   9 │ Ω.L[5,2]     0.0261588   0.366052     0.00538327   4345.52  2064.09     1.00291      3.3497
  10 │ Ω.L[3,3]     0.775999    0.148672     0.00348151   1845.72  2482.95     1.00082      1.42276
  11 │ Ω.L[4,3]    -0.0330662   0.349329     0.00604209   3242.42  2090.97     1.00099      2.49939
  12 │ Ω.L[5,3]     0.0374594   0.360744     0.00516219   4901.98  2431.25     1.00176      3.77865
  13 │ Ω.L[4,4]     0.753896    0.150472     0.00357772   1850.93  2236.89     1.00165      1.42677
  14 │ Ω.L[5,4]     0.0116934   0.349883     0.00506856   4664.43  2772.27     1.00128      3.59553
  15 │ Ω.L[5,5]     0.684545    0.179677     0.00469272   1541.5   1667.6      1.00377      1.18825
  16 │ σ            7.08991     0.392342     0.00609954   4281.99  2994.66     1.00037      3.30073
  17 │ τ[1]         3.82687     0.792461     0.0243249    1071.64  1274.54     1.00157      0.82606
  18 │ τ[2]         0.515217    0.457244     0.0118942    1162.98  1701.28     1.00367      0.896471
  19 │ τ[3]         1.57042     0.675595     0.0194601    1075.05  1066.81     1.00327      0.82869
  20 │ τ[4]         0.79098     0.502001     0.0137349    1042.75   683.387    1.0037       0.803794
  21 │ τ[5]         0.536124    0.435909     0.0118638    1106.15  1058.94     1.00122      0.852668
  22 │ γ[1,1]       5.1869      2.19555      0.0618344    1249.75  1539.01     1.00063      0.963357
  23 │ γ[2,1]      -0.104914    4.6473       0.0843589    3038.11  2765.66     0.999955     2.3419
  24 │ γ[3,1]      -2.26726     3.24333      0.0677281    2307.05  2102.85     1.00399      1.77836
  25 │ γ[4,1]       0.786036    4.18682      0.0682086    3757.86  2648.24     1.00005      2.89671
  26 │ γ[5,1]       0.317867    4.53047      0.067744     4456.83  2826.46     1.0041       3.43551
  27 │ γ[1,2]       5.68517     2.38212      0.0679177    1209.5   1530.76     1.00015      0.932333
  28 │ γ[2,2]       0.406946    4.69823      0.0761723    3785.93  2816.48     1.00131      2.91835
  29 │ γ[3,2]      -2.43749     3.41662      0.0695933    2451.7   2481.02     1.00083      1.88987
  30 │ γ[4,2]       1.40997     4.31934      0.0742324    3389.91  2550.09     1.00076      2.61308
  31 │ γ[5,2]      -0.565495    4.69425      0.0822518    3281.19  2340.3      1.00369      2.52928

We can see that we also get all of the Cholesky factors of the correlation matrix Ω which we can transform back into a correlation matrix by doing Ω = Ω.L * Ω.L'.

References

Boatwright, P., McCulloch, R., & Rossi, P. (1999). Account-level modeling for trade promotion: An application of a constrained parameter hierarchical model. Journal of the American Statistical Association, 94(448), 1063–1073.

de Finetti, B. (1974). Theory of Probability (Volume 1). New York: John Wiley & Sons.

Nau, R. F. (2001). De Finetti was Right: Probability Does Not Exist. Theory and Decision, 51(2), 89–124. https://doi.org/10.1023/A:1015525808214

Last modified: January 29, 2024. Website built with Franklin.jl and the Julia programming language.