Bonus: Epidemiological Models using ODE Solvers in Turing

Ok, now this is something that really makes me very excited with Julia's ecosystem. If you want to use an Ordinary Differential Equation solver in your Turing model, you don't need to code it from scratch. You've just borrow a pre-made one from DifferentialEquations.jl. This is what makes Julia so great. We can use functions and types defined in other packages into another package and it will probably work either straight out of the bat or without much effort!

For this tutorial I'll be using Brazil's COVID data from the Media Consortium. For reproducibility, we'll restrict the data to the year of 2020:

using Downloads
using DataFrames
using CSV
using Chain
using Dates

url = "https://data.brasil.io/dataset/covid19/caso_full.csv.gz"
file = Downloads.download(url)
df = DataFrame(CSV.File(file))
br = @chain df begin
    filter(
        [:date, :city] =>
            (date, city) ->
                date < Dates.Date("2021-01-01") &&
                    date > Dates.Date("2020-04-01") &&
                    ismissing(city),
        _,
    )
    groupby(:date)
    combine(
        [
            :estimated_population_2019,
            :last_available_confirmed_per_100k_inhabitants,
            :last_available_deaths,
            :new_confirmed,
            :new_deaths,
        ] .=>
            sum .=> [
                :estimated_population_2019,
                :last_available_confirmed_per_100k_inhabitants,
                :last_available_deaths,
                :new_confirmed,
                :new_deaths,
            ],
    )
end;

Let's take a look in the first observations

first(br, 5)

5×6 DataFrame
 Row │ date        estimated_population_2019  last_available_confirmed_per_100k_inhabitants  last_available_deaths  new_confirmed  new_deaths
     │ Date        Int64                      Float64                                        Int64                  Int64          Int64
─────┼────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
   1 │ 2020-04-02                  210147125                                        79.6116                    305           1167          61
   2 │ 2020-04-03                  210147125                                        90.9596                    365           1114          60
   3 │ 2020-04-04                  210147125                                       103.622                     445           1169          80
   4 │ 2020-04-05                  210147125                                       115.594                     496           1040          51
   5 │ 2020-04-06                  210147125                                       125.766                     569            840          73

Also the bottom rows

last(br, 5)

5×6 DataFrame
 Row │ date        estimated_population_2019  last_available_confirmed_per_100k_inhabitants  last_available_deaths  new_confirmed  new_deaths
     │ Date        Int64                      Float64                                        Int64                  Int64          Int64
─────┼────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
   1 │ 2020-12-27                  210147125                                      1.22953e5                 191250          17614         337
   2 │ 2020-12-28                  210147125                                      1.23554e5                 191788          27437         538
   3 │ 2020-12-29                  210147125                                      1.24291e5                 192839          56371        1051
   4 │ 2020-12-30                  210147125                                      1.25047e5                 194056          55600        1217
   5 │ 2020-12-31                  210147125                                      1.25724e5                 195072          54469        1016

Here is a plot of the data:

using AlgebraOfGraphics
using CairoMakie
f = Figure()
plt = data(br) * mapping(:date => L"t", :new_confirmed => "infected daily") * visual(Lines)
draw!(f[1, 1], plt)

The Susceptible-Infected-Recovered (SIR) (Grinsztajn, Semenova, Margossian & Riou, 2021) model splits the population in three time-dependent compartments: the susceptible, the infected (and infectious), and the recovered (and not infectious) compartments. When a susceptible individual comes into contact with an infectious individual, the former can become infected for some time, and then recover and become immune. The dynamics can be summarized in a system ODEs:

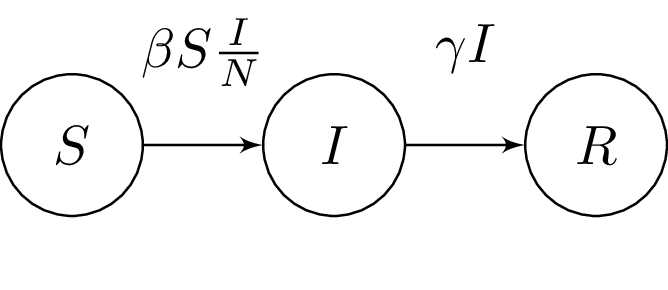
where:

• $S(t)$ – the number of people susceptible to becoming infected (no immunity)

• $I(t)$ – the number of people currently infected (and infectious)

• $R(t)$ – the number of recovered people (we assume they remain immune indefinitely)

• $\beta$ – the constant rate of infectious contact between people

• $\gamma$ – constant recovery rate of infected individuals

How to code an ODE in Julia?

It's very easy:

1. Use DifferentialEquations.jl

2. Create a ODE function

3. Choose:

   • Initial Conditions – $u_0$

   • Parameters – $p$

   • Time Span – $t$

   • Optional – Solver or leave blank for auto

PS: If you like SIR models checkout epirecipes/sir-julia

The following function provides the derivatives of the model, which it changes in-place. State variables and parameters are unpacked from u and p; this incurs a slight performance hit, but makes the equations much easier to read.

using DifferentialEquations

function sir_ode!(du, u, p, t)
    (S, I, R) = u
    (β, γ) = p
    N = S + I + R
    infection = β * I * S / N
    recovery = γ * I
    @inbounds begin
        du[1] = -infection # Susceptible
        du[2] = infection - recovery # Infected
        du[3] = recovery # Recovered
    end
    return nothing
end;

This is what the infection would look with some fixed β and γ in a timespan of 100 days starting from day one with 1,167 infected (Brazil in April 2020):

i₀ = first(br[:, :new_confirmed])
N = maximum(br[:, :estimated_population_2019])

u = [N - i₀, i₀, 0.0]
p = [0.5, 0.05]
prob = ODEProblem(sir_ode!, u, (1.0, 100.0), p)
sol_ode = solve(prob)
f = Figure()
plt =
    data(stack(DataFrame(sol_ode), Not(:timestamp))) *
    mapping(
        :timestamp => L"t",
        :value => L"N";
        color=:variable => renamer(["value1" => "S", "value2" => "I", "value3" => "R"]),
    ) *
    visual(Lines; linewidth=3)
draw!(f[1, 1], plt; axis=(; title="SIR Model for 100 days, β = $(p[1]), γ = $(p[2])"))

How to use a ODE solver in a Turing Model

Please note that we are using the alternative negative binomial parameterization as specified in 8. Bayesian Regression with Count Data:

function NegativeBinomial2(μ, ϕ)
    p = 1 / (1 + μ / ϕ)
    r = ϕ

    return NegativeBinomial(r, p)
end

NegativeBinomial2 (generic function with 1 method)

Now this is the fun part. It's easy: just stick it inside!

using Turing
using LazyArrays
using Random: seed!
seed!(123)

@model function bayes_sir(infected, i₀, r₀, N)
    #calculate number of timepoints
    l = length(infected)

    #priors
    β ~ TruncatedNormal(2, 1, 1e-4, 10)     # using 10 because numerical issues arose
    γ ~ TruncatedNormal(0.4, 0.5, 1e-4, 10) # using 10 because numerical issues arose
    ϕ⁻ ~ truncated(Exponential(5); lower=0, upper=1e5)
    ϕ = 1.0 / ϕ⁻

    #ODE Stuff
    I = i₀
    u0 = [N - I, I, r₀] # S,I,R
    p = [β, γ]
    tspan = (1.0, float(l))
    prob = ODEProblem(sir_ode!, u0, tspan, p)
    sol = solve(
        prob,
        Tsit5(); # similar to Dormand-Prince RK45 in Stan but 20% faster
        saveat=1.0,
    )
    solᵢ = Array(sol)[2, :] # New Infected
    solᵢ = max.(1e-4, solᵢ) # numerical issues arose

    #likelihood
    return infected ~ arraydist(LazyArray(@~ NegativeBinomial2.(solᵢ, ϕ)))
end;

Now run the model and inspect our parameters estimates. We will be using the default NUTS() sampler with 1_000 samples on only one Markov chain:

infected = br[:, :new_confirmed]
r₀ = first(br[:, :new_deaths])
model_sir = bayes_sir(infected, i₀, r₀, N)
chain_sir = sample(model_sir, NUTS(), 1_000)
summarystats(chain_sir[[:β, :γ]])

Summary Statistics
  parameters      mean       std      mcse   ess_bulk   ess_tail      rhat   ess_per_sec
      Symbol   Float64   Float64   Float64    Float64    Float64   Float64       Float64

           β    1.1199    0.0292    0.0013   477.2173   505.0551    0.9996       11.2615
           γ    1.0869    0.0296    0.0014   477.1981   493.8323    0.9996       11.2610

Hope you had learned some new bayesian computational skills and also took notice of the amazing potential of Julia's ecosystem of packages.

References

Grinsztajn, L., Semenova, E., Margossian, C. C., & Riou, J. (2021). Bayesian workflow for disease transmission modeling in Stan. ArXiv:2006.02985 [q-Bio, Stat]. http://arxiv.org/abs/2006.02985