O que é Estatística Bayesiana?

Noções de Probabilidade, Estatística Frequentista versus Estatística Bayesiana

A estatística Bayesiana¹ é uma abordagem de análise de dados baseada no teorema de Bayes, onde o conhecimento disponível sobre os parâmetros em um modelo estatístico é atualizado com as informações dos dados observados (Gelman et al., 2013). O conhecimento prévio é expresso como uma distribuição a priori² e combinado com os dados observados na forma de uma função de verossimilhança³ para determinar a distribuição a posteriori⁴ . A posteriori também pode ser usada para fazer previsões sobre eventos futuros.

Estatística Bayesiana está revolucionando todos os campos das ciências baseadas em evidências⁵ (van de Schoot et al., 2021). A insatisfação com métodos tradicionais de inferência estatística (estatística frequentista) e o advento dos computadores com o crescimento exponencial de poder computacional⁶ proporcionaram a ascensão da estatística Bayesiana por ser uma abordagem alinhada com a intuição humana de incerteza, robusta à más-práticas científicas, porém computacionalmente intensiva.

Porém antes de entrarmos em estatística Bayesiana, temos que falar de probabilidade: o motor da inferência Bayesiana.

O que é probabilidade?

PROBABILIDADE NÃO EXISTE!

de Finetti (1974)⁷

Essas são as primeiras palavras no prefácio do célebre livro de Bruno de Finetti (figura 1), um dos mais importantes matemáticos e filósofos da probabilidade. Sim, a probabilidade não existe. Ou melhor, probabilidade como uma quantidade física, chance objetiva, NÃO existe. De Finetti mostrou que, em certo sentido preciso, se dispensarmos a questão da chance objetiva nada se perde. A matemática do raciocínio indutivo permanece exatamente a mesma.

Figure 1: Bruno de Finetti. Figura de https://www.wikipedia.org

Considere jogar uma moeda de enviesada. As tentativas são consideradas independentes e, como resultado, exibem outra propriedade importante: a ordem não importa. Dizer que a ordem não importa é dizer que se você pegar qualquer sequência finita de cara e coroa e permutar os resultados da maneira que quiser, a sequência resultante terá a mesma probabilidade. Dizemos que essa probabilidade é invariante sob permutações.

Ou, dito de outra forma, a única coisa que importa é a frequência relativa. As sequências de resultados que têm as mesmas frequências de cara e coroa consequentemente possuem a mesma probabilidade. A frequência é considerada uma estatística suficiente⁸. Dizer que a ordem não importa ou dizer que a única coisa que importa é a frequência são duas maneiras de dizer exatamente a mesma coisa. Essa propriedade é chamada de permutabilidade por de Finetti. E é a mais importantes propriedade da probabilidade que faz com que possamos manipulá-la matematicamente (ou filosoficamente) mesmo que ela não exista como uma “coisa” física.

Ainda desenvolvendo o argumento: “O raciocínio probabilístico –sempre entendido como subjetivo– decorre apenas da incerteza de algo. Não faz diferença se a incerteza diz respeito a um futuro imprevisível⁹, ou a um passado despercebido, ou a um passado duvidosamente relatado ou esquecido¹⁰… A única coisa relevante é a incerteza – a extensão de nosso próprio conhecimento e ignorância. O fato real de se os eventos considerados são ou não determinados em algum sentido, ou conhecidos por outras pessoas, e assim por diante, é irrelevante” (tradução minha de de Finetti (1974)).

Concluindo: não importa o que é probabilidade, você consegue usá-la de qualquer maneira, mesmo que ela seja um frequência absoluta (ex: probabilidade de eu plantar bananeira de sunga na Avenida Paulista é ZERO pois a probabilidade de um evento que nunca ocorreu ocorrer no futuro é ZERO) ou um palpite subjetivo (ex: talvez a probabilidade não seja ZERO, mas 0,00000000000001; bem improvável, mas não impossível).

Definição Matemática

Com a intuição filosófica de probabilidade elaborada, vamos às intuições matemáticas. A probabilidade de um evento é um número real¹¹ entre 0 e 1, onde, grosso modo, 0 indica a impossibilidade do evento e 1 indica a certeza do evento. Quanto maior a probabilidade de um evento, mais provável é que o evento ocorrerá. Um exemplo simples é o lançamento de uma moeda justa (imparcial). Como a moeda é justa, os dois resultados (“cara” e “coroa”) são igualmente prováveis; a probabilidade de “cara” é igual à probabilidade de “coroa”; e uma vez que nenhum outro resultado é possível, a probabilidade de “cara” ou “coroa” é \(\frac{1}{2}\) (que também pode ser escrita como 0,5 ou 50%).

Sobre notação, definimos que \(A\) é um evento e \(P(A)\) a probabilidade do evento, logo:

\[ \{P(A) \in \mathbb{R} : 0 \leq P(A) \leq 1 \}. \]

Isto quer dizer o “probabilidade do evento \(A\) ocorrer é o conjunto de todos os números reais entre 0 e 1; incluindo 0 e 1.” Além disso temos três axiomas¹², oriundos de Kolmogorov (1933) (figura 2):

1. Não-negatividade: Para todo \(A\), \(P(A) \geq 0\). Toda probabilidade é positiva (maior ou igual a zero), independente do evento.
2. Aditividade: Para dois mutuamente exclusivos \(A\) e \(B\) (não podem ocorrer ao mesmo tempo¹³): \(P(A) = 1 - P(B)\) e \(P(B) = 1 - P(A)\).
3. Normalização: A probabilidade de todos os eventos possíveis \(A_1, A_2, \dots\) devem somar 1: \(\sum_{n \in \mathbb{N}} A_n = 1\).

Figure 2: Andrey Nikolaevich Kolmogorov. Figura de https://www.wikipedia.org

Com esses três simples (e intuitivos) axiomas, conseguimos derivar e construir toda a matemática da probabilidade.

Probabilidade Condicional

Um conceito importante é a probabilidade condicional que podemos definir como “probabilidade de um evento ocorrer caso outro tenha ocorrido ou não.” A notação que usamos é \(P( A \mid B )\), que lê-se como “a probabilidade de observamos \(A\) dado que já observamos \(B\).”

Um bom exemplo é o jogo de Poker Texas Hold’em, onde o jogador recebe duas cartas e podem utilizar mais cinco cartas comunitárias para montar sua “mão.” A probabilidade de você receber um Rei (\(K\)) é \(\frac{4}{52}\):

\[ P(K) = \left(\frac{4}{52}\right) = \left(\frac{1}{13}\right). \]

E a probabilidade de você receber um Ás (\(A\)) também é \(\frac{4}{52}\):

\[ P(A) = \left(\frac{4}{52}\right) = \left(\frac{1}{13}\right). \]

Porém a probabilidade de você receber um Rei como segunda carta dado que você recebeu um Ás como primeira carta é:

\[ P(K \mid A) = \left(\frac{4}{51}\right). \]

Como temos uma carta a menos (\(52 - 1 = 51\)) já que você recebeu o Ás (visto que \(A\) foi observado), temos 4 Reis ainda no baralho, logo \(\frac{4}{51}\).

Probabilidade Conjunta

Probabilidade condicional nos leva à um outro conceito importante: probabilidade conjunta. Probabilidade conjunta é a “probabilidade de observados dois eventos ocorrem.” Continuando no nosso exemplo do Poker, a probabilidade de você receber como duas cartas iniciais um Ás (\(A\)) e um Rei (\(K\)) é:

\[ \begin{aligned} P(A,K) &= P(A) \cdot P(K \mid A) \\ &= P \left(\frac{1}{13}\right) \cdot P \left(\frac{4}{51}\right)\\ &= P \left(\frac{4}{51 \cdot 13}\right) \\ &\approx 0.006. \end{aligned} \]

Note que \(P(A,K) = P(K,A)\):

\[ \begin{aligned} P(K,A) &= P(K) \cdot P(A \mid K) \\ &= P \left(\frac{1}{13}\right) \cdot P \left(\frac{4}{51}\right)\\ &= P \left(\frac{4}{51 \cdot 13}\right) \\ &\approx 0.006. \end{aligned} \]

No nosso exemplo de Poker temos uma certa simetria:

\[ P(K \mid A) = P(A \mid K). \]

Mas sem sempre essa simetria existe (na verdade muito raramente ela existe). A identidade que temos é a seguinte:

\[ P(A) \cdot P(K \mid A) = P(K) \cdot P(A \mid K). \]

Então essa simetria só existe quando as taxas basais dos eventos condicionais são iguais:

\[ P(A) = P(K). \]

Que é o que ocorre no nosso exemplo.

Probabilidade Condicional não é “comutativa”

\[P(A \mid B) \neq P(B \mid A)\]

Veja um exemplo prático. Digamos que eu estou me sentindo bem e começo a tossir na fila do mercado. O que você acha que irá acontecer? Todo mundo vai achar que estou com COVID, o que é equivalente à pensar em \(P(\text{tosse} \mid \text{covid})\). Vendo os sintomas mais comuns do COVID, caso você esteja com COVID, a chance de você tossir é muito alta. Mas na verdade tossimos muito mais frequentemente que temos COVID – \(P(\text{tosse}) \neq P(\text{COVID})\), logo:

\[ P(\text{COVID} \mid \text{tosse}) \neq P(\text{tosse} \mid \text{COVID}). \]

Teorema de Bayes

Este é o ultimo conceito de probabilidade que precisamos abordar antes de mergulhar na estatística Bayesiana¹⁴, mas é o mais importante. Note que não é coincidência semântica que estatística Bayesiana e teorema de Bayes possuem o mesmo prefixo.

Thomas Bayes (1701 - 1761, figura 3) foi um estatístico, filósofo e ministro presbiteriano inglês conhecido por formular um caso específico do teorema que leva seu nome: o teorema de Bayes. Bayes nunca publicou o que se tornaria sua realização mais famosa; suas notas foram editadas e publicadas após sua morte pelo seu amigo Richard Price¹⁵. Em seus últimos anos, Bayes se interessou profundamente por probabilidade. Alguns especulam que ele foi motivado a refutar o argumento de David Hume contra a crença em milagres com base nas evidências do testemunho em “An Inquiry Concerning Human Understanding.”

Figure 3: Thomas Bayes. Figura de https://www.wikipedia.org

Vamos logo para o Teorema. Lembra que temos a seguinte identidade na probabilidade:

\[ \begin{aligned} P(A,B) &= P(B,A) \\ P(A) \cdot P(B \mid A) &= P(B) \cdot P(A \mid B). \end{aligned} \]

Pois bem, agora passe o \(P(B)\) do lado direito para o lado esquerdo dividindo:

\[ \begin{aligned} P(A) \cdot P(B \mid A) &= \overbrace{P(B)}^{\text{isso vai para $\leftarrow$}} \cdot P(A \mid B) \\ &\\ \frac{P(A) \cdot P(B \mid A)}{P(B)} &= P(A \mid B) \\ P(A \mid B) &= \frac{P(A) \cdot P(B \mid A)}{P(B)}. \end{aligned} \]

E esse é o resultado final:

\[ P(A \mid B) = \frac{P(A) \cdot P(B \mid A)}{P(B)}. \]

A estatística Bayesiana usa esse teorema como motor de inferência dos parâmetros de um modelo condicionado aos dados observados.

Parâmetros Discretos vs Contínuos

Tudo o que foi exposto até agora partiu do pressuposto que os parâmetros são discretos. Isto foi feito com o intuito de prover uma melhor intuição do que é probabilidade. Nem sempre trabalhamos com parâmetros discretos. Os parâmetros podem ser contínuos, como por exemplo: idade, altura, peso etc. Mas não se desespere, todas as regras e axiomas da probabilidade são válidos também para parâmetros contínuos. A única coisa que temos que fazer é trocar todas as somas \(\sum\) por integrais \(\int\). Por exemplo o terceiro axioma de Normalização para variáveis aleatórias contínuas se torna:

\[ \int_{x \in X} p(x) dx = 1. \]

Estatística Bayesiana

Agora que você já sabe o que é probabilidade e o que é o teorema de Bayes, vou propor o seguinte modelo:

\[ \underbrace{P(\theta \mid y)}_{\textit{Posteriori}} = \frac{\overbrace{P(y \mid \theta)}^{\text{Verossimilhança}} \cdot \overbrace{P(\theta)}^{\textit{Priori}}}{\underbrace{P(y)}_{\text{Constante Normalizadora}}}, \]

onde:

• \(\theta\) – parâmetro(s) de interesse
• \(y\) – dados observados
• Priori – probabilidade prévia do valor do(s) parâmetro(s)¹⁶
• Verossimilhança – probabilidade dos dados observados condicionados aos valores do(s) parâmetro(s)
• Posteriori – probabilidade posterior do valor do(s) parâmetros após observamos os dados \(y\)
• Constante Normalizadora – \(P(y)\) não faz sentido intuitivo. Essa probabilidade é transformada e pode ser interepretada como algo que existe apenas para que o resultado de \(P(y \mid \theta) P(\theta)\) seja algo entre 0 e 1 – uma probabilidade válida. Vamos falar mais sobre essa constante na Aula 5 - Markov Chain Montecarlo – MCMC

A estatísica Bayesiana nos permite quantificar diretamente a incerteza relacionada ao valor de um ou mais parâmetros do nosso modelo condicionado aos dados observados. Isso é a característica principal da estatística Bayesiana. Pois estamos estimando diretamente \(P(\theta \mid y)\) por meio do teorema de Bayes. A estimativa resultante é totalmente intuitiva: simplesmente quantifica a intercerteza que temos sobre o valor de um ou mais parâmetro condicionado nos dados, nos pressupostos do nosso modelo (verossimilhança) e na probabilidade prévia que temos sobre tais valores.

Estatística Frequentista

Para contrastar com a estatística Bayesiana, vamos ver como a estatística clássica frequentista¹⁷. E já aviso, não é algo intuitivo que nem a estatística Bayesiana.

Para a estatística frequentista o pesquisador está proibido de fazer conjecturas probabilísticas sobre parâmetros. Pois eles não são incertos, muito pelo contrário é uma quantidade determinada. A única questão é que não observamos diretamente os parâmetros, mas eles são determinísticos e não permitem qualquer margem de incerteza. Logo, para a abordagem frequentista, parâmetros são quantidades de interesse não observadas na qual não fazemos conjecturas probabilísticas.

O que é então incerto na estatística frequentista? Resposta curta: os dados observados. Para a abordagem frequentista a sua amostra é incerta. É sobre ela que você pode fazer conjecturas probabilísticas. Portanto, a incerteza é expressa na probabilidade de eu obter dados similares aos que eu obtive se eu amostrasse de uma população de interesse infinitas amostras do mesmo tamanho que a minha amostra¹⁸. A incerteza é condicionada à uma abordagem frequentista, em outras palavras, a incerteza só existe se eu considerar um processo de amostragem infinito e extrair desse processo uma frequência. A probabilidade só existe se representar uma frequência. Mesmo se isso ocasionar em um “processo de amostragem infinito de uma população que eu nunca observei,” por mais estranho que isso soe¹⁹.

Para a abordagem frequentista não existe probabilidade posteriori nem priori pois ambas envolvem parâmetros, e vimos que isso é proibido em solo frequentista. Tudo o que é necessário para a inferência estatística está contida na verossimilhança²⁰.

Além disso, por razões de facilidade de computação, pois boa parte desses métodos foram inventados na primeira métade do século XX (sem a ajuda do computador), apenas é computado o valor dos parâmetros que maximizam a função da verossimilhança²¹. Desse processo de otimização extraímos a moda da verossimilhança (i.e. o valor máximo). A estimativa de maximização da verossimilhança é o valor dos parâmetros de forma que a amostra de tamanho \(N\) amostrada de maneira aleatória de uma população (os dados que você tem) é a amostra de tamanho \(N\) mais provável da população. Todas as outras amostras potenciais que poderiam ser extraídos dessa população terão uma estimação pior do que a amostra que você realmente tem²². Em outras palavras, estamos condicionando o(s) valor(es) dos parâmetro(s) aos dados observados, partindo do pressuposto de que estamos amostrando amostras infinitas de tamanho \(N\) de uma população teórica e tratando os valores dos parâmetros como fixos e nossa amostra como aleatória (ou incerta).

A moda funciona perfeitamente no mundo de conto de fadas que se pressupõe que tudo segue uma distribuição normal, pois a moda é igual a mediana e a média – \(\text{média} = \text{mediana} = \text{moda}\). Só tem um problema, raramente esse pressuposto é verdadeiro (figura 4), ainda mais quando falamos de parâmetros num contexto de pluralidade de parâmetros e relações complexas entre parâmetros (modelos complexos).

Figure 4: Pressupostos vs Realidade. Figura de Katherine Hoffman. Reprodução Autorizada.

Vale aqui uma breve explicação sociológica e computacional porque a estatística clássica proíbe conjecturas probabilísticas sobre parâmetros e trabalhamos com otimização (achar o valor máximo de uma função) do que aproximação ou estimação da densidade completa da verossimilhança (em outras palavras, “levantar a capivara toda” da verossimilhança ao invés de somente a moda).

Sobre a questão sociológica, a ciência no começo do século XX partia do princípio que ela é objetiva e toda subjetividade deve ser banida. Logo, como a estimação da probabilidade a posteriori de parâmetros envolve a elucidação de uma probabilidade a priori de parâmetros, tal método não deve ser permitido na ciência, pois traz subjetividade (sabemos hoje que nada no comportamento humano é puramente objetivo, e a subjetividade impregna todas as empreitadas humanas).

Sobre a questão computacional, na década de 1930s sem computadores era muito mais fácil usar pressupostos fortes sobre os dados para conseguir uma resposta de uma estimação estatística usando derivações matemáticas do que calcular na mão a estimação estatística sem depender de tais pressupostos. Por exemplo: o famoso teste \(t\) de Student é um teste que indica quando conseguimos rejeitar que a média de um certo parâmetro de interesse entre dois grupos é igual (famosa hipótese nula – \(H_0\)). Esse teste parte do pressuposto que se o parâmetro de interesse for distribuído conforme uma distribuição normal (pressuposto 1 – normalidade da variável dependente), se a variância do parâmetro de interesse varia de maneira homogênea dentre os grupos (pressuposto 2 – homogeneidade das variâncias) e se o número de observações nos dois grupos de interesse é similar (pressuposto 3 – homogeneidade do tamanho dos grupos) a diferença entre os grupos ponderada pela variância dos grupos segue uma distribuição \(t\) de Student (por isso o nome do teste).

Então a estimação estatística se resume a calcular a média de dois grupos, a variância de cada um deles para um parâmetro de interesse e buscar o tal do \(p\)-valor numa tabela e ver se conseguimos rejeitar a \(H_0\). Isto é válido quando tudo o que fazemos é calculado na mão, hoje com um computador 1 milhão de vezes mais potente que o computador da Apollo 11 (levou a humanidade à lua) no seu bolso²³, não sei se ainda é valido.

\(p\)-valores

\(p\)-valores são de difícil entendimento, \(p < 0.05\).

Já que mencionamos \(p\)-valor, vamos então explicar o que é o \(p\)-valor. Primeiramente a definição estatística:

\(p\)-valor é a probabilidade de obter resultados no mínimo tão extremos quanto os que foram observados, dado que a hipótese nula \(H_0\) é verdadeira.

Se você escrever essa definição em qualquer prova, livro ou artigo científico, você estará 100% preciso e correto na definição do que é um \(p\)-valor. Agora, a compreensão dessa definição é algo complicado. Para isso, vamos quebrar essa definição em algumas partes para melhor compreensão:

• “probabilidade de obter resultados…”: vejam que \(p\)-valores são uma característica dos seus dados e não da sua teoria ou hipótese.
• “…no mínimo tão extremos quanto os que foram observados…”: “no minimo tão” implica em definir um limiar para a caracterização de algum achado relevante, que é comumente chamado de \(\alpha\). Geralmente estipulamos alpha em 5% (\(\alpha = 0.05\)) e qualquer coisa mais extrema que alpha (ou seja menor que 5%) caracterizamos como significante.
• “…dado que a hipótese nula é verdadeira.”: todo teste estatístico que possui um \(p\)-valor possui uma Hipótese Nula (geralmente escrita como \(H_0\)). Hipótese nula, sempre tem a ver com algum efeito nulo. Por exemplo, a hipótese nula do teste Shapiro-Wilk e Komolgorov-Smirnov é “os dados são distribuídos conforme uma distribuição Normal” e a do teste de Levene é “as variâncias dos dados são iguais.” Sempre que ver um \(p\)-valor, se pergunte: “Qual a hipótese nula que este teste presupõe correta?”

Para entender o \(p\)-valor qualquer teste estatístico primeiro descubra qual é a hipótese nula por trás daquele teste. A definição do \(p\)-valor não mudará. Em todo teste ela é sempre a mesma. O que muda com o teste é a hipótese nula. Cada teste possui sua \(H_0\). Por exemplo, alguns testes estatísticos comuns (\(\text{D}\) = dados):

• Teste t: \(P(D \mid \text{a diferença entre os grupos é zero})\)
• ANOVA: \(P(D \mid \text{não há diferença entre os grupos})\)
• Regressão: \(P(D \mid \text{coeficiente é nulo})\)
• Shapiro-Wilk: \(P(D \mid \text{amostra é normal})\)

\(p\)-valor é a probabilidade dos dados que você obteve dado que a hipótese nula é verdadeira. Para os que gostam do formalismo matemático: \(p = P(D \mid H_0)\). Em português, essa expressão significa “a probabilidade de \(D\) condicionado à \(H_0\).” Antes de avançarmos para alguns exemplos e tentativas de formalizar uma intuição sobre os \(p\)-valores, é importante ressaltar que \(p\)-valores dizem algo à respeito dos dados e não de hipóteses. Para o \(p\)-valor, a hipótese nula é verdadeira, e estamos apenas avaliando se os dados se conformam à essa hipótese nula ou não. Se vocês saírem desse tutorial munidos com essa intuição, o mundo será agraciado com pesquisadores mais preparados para qualificar e interpretar evidências (\(p < 0.05\)).

Exemplo intuitivo:

Imagine que você tem uma moeda que suspeita ser enviesada para uma probabilidade maior de dar cara. (Sua hipótese nula é então que a moeda é justa.) Você joga a moeda 100 vezes e obtém mais cara do que coroa. O \(p\)-valor não dirá se a moeda é justa, mas dirá a probabilidade de você obter pelo menos tantas caras quanto se a moeda fosse justa. É isso - nada mais.

Apesar de mencionar anteriormente que definições intuitivas não são precisas, elas sem dúvida facilitam o entendimento do \(p\)-valor.

\(p\)-valores – Algumas questões históricas

Não tem como entendermos \(p\)-valores se não compreendermos as suas origens e trajetória histórica. A primeira menção do termo foi feita pelo estatístico Ronald Fisher[A controvérsia da personalidade e vida de Ronald Fisher merece uma nota de rodapé. Suas contribuições, sem dúvida, foram cruciais para o avanço da ciência e da estatística. Seu intelecto era brilhante e seu talento já floresceu jovem: antes de completar 33 anos de idade ele tinha proposto o método de estimação por máxima verossimilhança (maximum likelihood estimation) (Stigler et al., 2007) e também criou o conceito de graus de liberdade (degrees of freedom) ao propor uma correção no teste de chi-quadrado de Pearson (Baird, 1983). Também inventou a Análise de Variância (ANOVA) e foi o primeiro a propor randomização como uma maneira de realizar experimentos, sendo considerado o “pai” dos ensaios clínicos randomizados. Nem tudo é florido na vida de Fisher, ele foi um eugenista e possuía uma visão muito forte sobre etnia e raça preconizando a superioridade de certas etnias. Além disso, era extremamente invariante, perseguindo, prejudicando e debochando qualquer crítico à suas teorias e publicações. O que vemos hoje no monopólio do paradigma Neyman-Pearson (Neyman & Pearson, 1933) com \(p\)-valores e hipóteses nulas é resultado desse esforço Fisheriano em calar os críticos e deixar apenas sua voz ecoar.] em 1925 (Fisher, 1925) que define o \(p\)-valor como um “índice que mede a força da evidência contra a hipótese nula.” Para quantificar a força da evidência contra a hipótese nula, Fisher defendeu “\(p<0.05\) (5% de significância) como um nível padrão para concluir que há evidência contra a hipótese testada, embora não como uma regra absoluta.” Fisher não parou por aí mas classificou a força da evidência contra a hipótese nula. Ele propôs “se \(p\) está entre 0.1 e 0.9, certamente não há razão para suspeitar da hipótese testada. Se estiver abaixo de 0.02, é fortemente indicado que a hipótese falha em explicar o conjunto dos fatos. Não seremos frequentemente perdidos se traçarmos uma linha convencional de 0.05” Desde que Fisher fez esta declaração há quase 100 anos, o limiar de 0.05 foi usado por pesquisadores e cientistas em todo o mundo e tornou-se ritualístico usar 0.05 como limiar como se outros limiares não pudessem ser usados.

Figure 5: Ronald Fisher. Figura de https://www.wikipedia.org

Após isso, o limiar de 0.05 agora instaurado como inquestionável influenciou fortemente a estatística e a ciência. Mas não há nenhuma razão contra a adoção de outros limiares (\(\alpha\)) como 0.1 ou 0.01 (Lakens et al., 2018). Se bem argumentados, a escolha de limiares diferentes de 0.05 pode ser bem-vista por editores, revisores e orientadores. Como o \(p\)-valor é uma probabilidade, ele é uma quantidade contínua. Não há razão para diferenciarmos um \(p\) de 0.049 contra um \(p\) de 0.051. Robert Rosenthal, um psicólogo já dizia “Deus ama \(p\) de 0.06 tanto quanto um \(p\) de 0.05” (Rosnow & Rosenthal, 1989).

No último ano de sua vida, Fisher publicou um artigo (Fisher, 1962) examinando as possibilidades dos métodos Bayesianos, mas com as probabilidades a priori a serem determinadas experimentalmente. Inclusive alguns autores especulam (Jaynes, 2003) que se Fisher estivesse vivo hoje, ele provavelmente seria um “Bayesiano.”

O que o \(p\)-valor não é

Com a definição e intuição do que é um \(p\)-valor bem ancoradas, podemos avançar para o que o \(p\)-valor não é!

1. \(p\)-valor não é a probabilidade da Hipótese nula - Famosa confusão entre \(P(D \mid H_0)\) e \(P(H_0 \mid D)\). \(p\)-valor não é a probabilidade da hipótese nula, mas sim a probabilidade dos dados que você obteve. Para obter a $P(H_0 D) você precisa de estatística Bayesiana.

2. \(p\)-valor não é a probabilidade dos dados serem produzidos pelo acaso - Não! Ninguém falou nada de acaso. Mais uma vez: \(p\)-valor é probabilidade de obter resultados no mínimo tão extremos quanto os que foram observados, dado que a hipótese nula é verdadeira.

3. \(p\)-valor mensura o tamanho do efeito de um teste estatístico - Também não… \(p\)-valor não diz nada sobre o tamanho do efeito. Apenas sobre se o quanto os dados observados divergem do esperado sob a hipótese nula. É claro que efeitos grandes são mais prováveis de serem estatisticamente significantes que efeitos pequenos. Mas isto não é via de regra e nunca julguem um achado pelo seu \(p\)-valor, mas sim pelo seu tamanho de efeito. Além disso, \(p\)-valores podem ser “hackeados” de diversas maneiras (Head, Holman, Lanfear, Kahn, & Jennions, 2015) e muitas vezes seu valor é uma consequência direta do tamanho da amostra.

Intervalos de Confiança

Para concluir, vamos falar sobre os famosos intervalos de confiança, que não são uma medida que quantifica a incerteza do valor de um parâmetro (lembre-se conjecturas probabilísticas sobre parâmetros são proibidos em frequentist-land). Segure seu queixo, intervalos de confiança são:

Um intervalo de confiança de X% para um parâmetro é um intervalo \((a, b)\) gerado por um procedimento que em amostragem repetida tem uma probabilidade de X% de conter o valor verdadeiro do parâmetro, para todos os valores possíveis do parâmetro

Neyman (1937) (o “pai” dos intervalos de confiança, figura 6)

Figure 6: Jerzy Neyman. Figura de https://www.wikipedia.org

Mais uma vez a ideia da amostragem repetida infinita vezes de uma população que você nunca viu. Por exemplo: digamos que você executou uma análise estatística para comparar eficácia de uma política pública em dois grupos e você obteve a diferença entre a média desses grupos. Você pode expressar essa diferença como um intervalo de confiança. Geralmente escolhemos a confiança de 95%. Você então escreve no seu artigo que a “diferença entre grupos observada é de 10.5 - 23.5 (95% IC).” Isso quer dizer que 95 estudos de 100, que usem o mesmo tamanho de amostra e população-alvo, aplicando o mesmo teste estatístico, esperarão encontrar um resultado de diferenças de média entre grupos entre 10.5 e 23.5. Aqui as unidades são arbitrárias, mas para continuar o exemplo vamos supor que sejam expectativa de vida.

Infelizmente com estatística frequentista você tem que escolher uma das duas qualidades para explicações: intuitiva ou precisa²⁴.

Intervalos de Confiança (Frequentista) vs Intervalos de Credibilidade (Bayesiana)

A estatística Bayesiana possui um conceito análogo ao de intervalos de confiança da estatística frequentista. Esse conceito se chama intervalo de credibilidade²⁵ e, ao contrário do intervalo de confiança, a sua definição é intuitiva. Intervalo de credibilidade mensura um intervalo no qual temos certeza que o valor do parâmetro de interesse é, com base na verossimilhança condicionada aos dados observados – \(P(y \mid \theta)\); e na probabilidade priori do parâmetro – \(P(\theta)\). Ele é basicamente uma “fatia” da probabilidade posteriori do parâmetro restrita a um certo nível de certeza. Por exemplo: um intervalo de credibilidade 95% mostra o intervalo que temos 95% de certeza que o valor do nosso parâmetro se encontra. Simples assim…

Para exemplificar veja na figura 7 que mostra uma distribuição Log-Normal com média 0 e desvio padrão 2. O gráfico na parte superior mostra a estimativa da máxima verossimilhança²⁶ do valor de \(\theta\) que é a moda da distribuição. E no gráfico de baixo temos o intervalo de credibilidade 50% do valor de \(\theta\) que é o intervalo entre o percentil 25% e o percentil 75%. Nesse exemplo, estimação por máxima verossimilhança nos leva à valores estimados que não são condizentes com a real densidade probabilística do valor de \(\theta\).

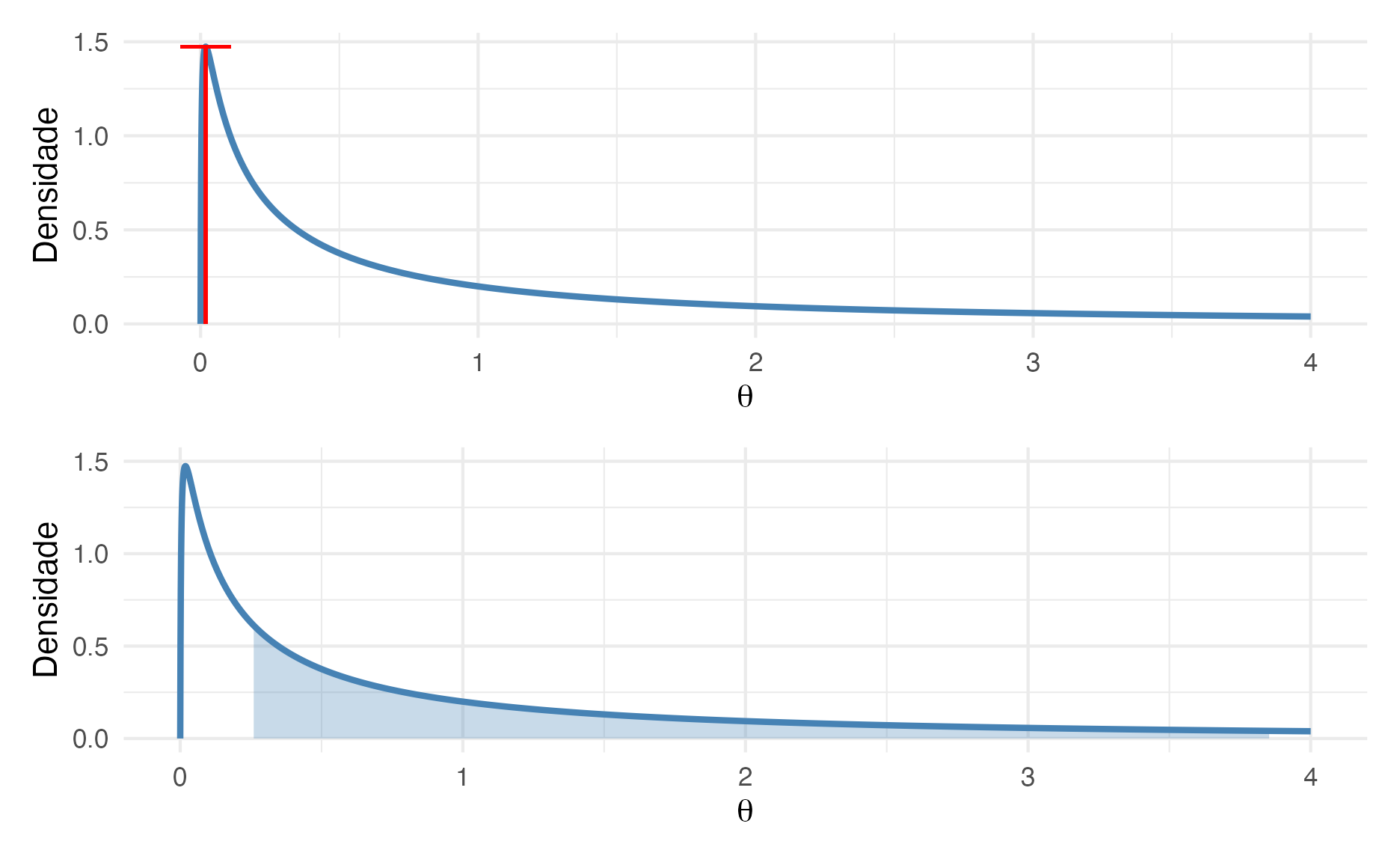
Figure 7: De baixo para cima: Estimação de Máxima Verossimilhança e Intervalo de Credibilidade

Agora um exemplo de uma distribuição multimodal²⁷. A figura 8 mostra uma distribuição bimodal com duas modas 2 e 10²⁸. O gráfico na parte superior mostra a estimativa da máxima verossimilhança do valor de \(\theta\) que é a moda da distribuição. Vejam que mesmo com 2 modas, maxima verossimilhança se “agarra” na maior moda²⁹. E no gráfico de baixo temos o intervalo de credibilidade 50% do valor de \(\theta\) que é o intervalo entre o percentil 25% e o percentil 75%. Nesse exemplo, estimação por máxima verossimilhança de novo nos leva à valores estimados que não são condizentes com a real densidade probabilística do valor de \(\theta\).

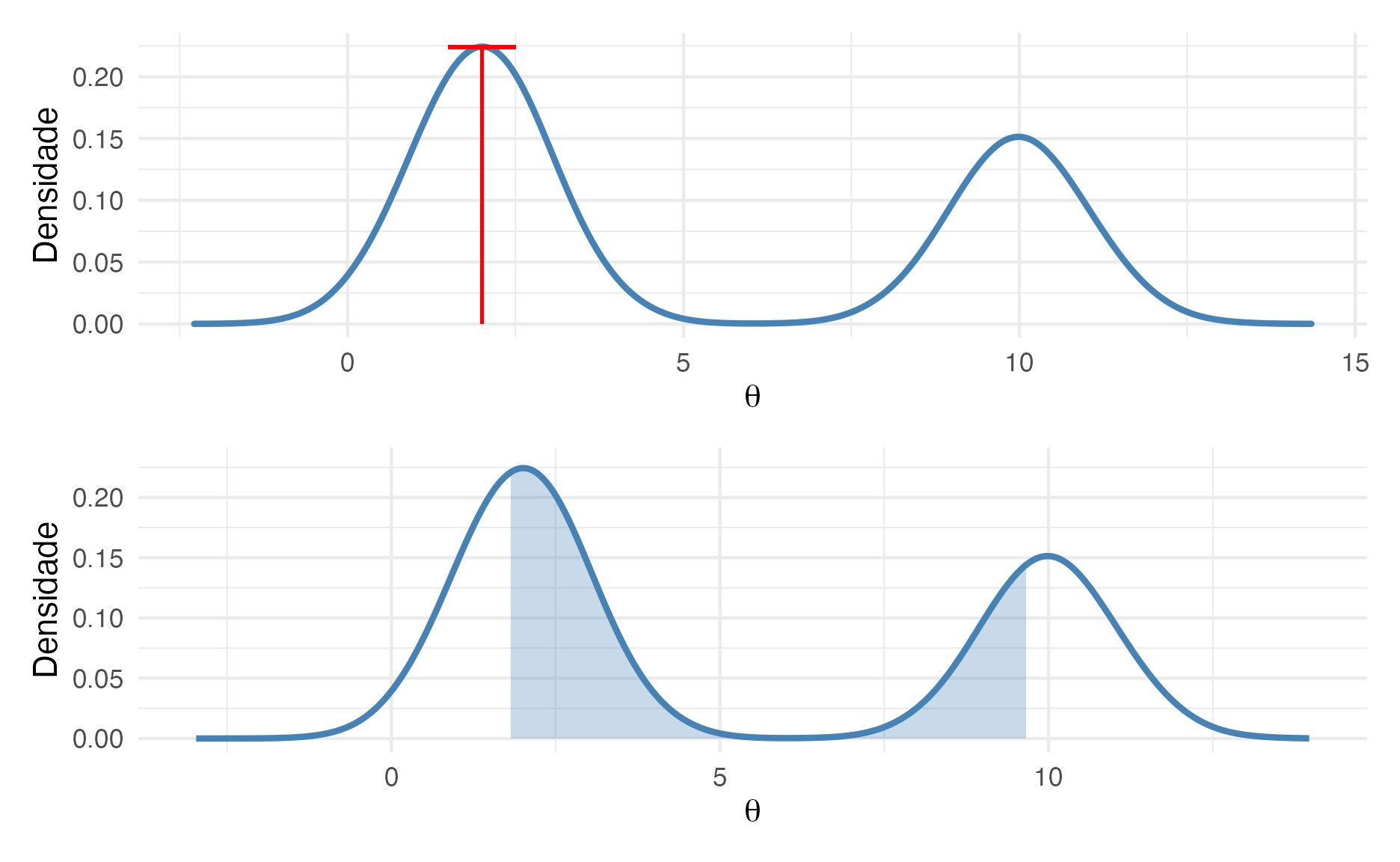
Figure 8: De baixo para cima: Estimação de Máxima Verossimilhança e Intervalo de Credibilidade

Estatística Bayesiana vs Frequentista

O que discutimos acima de resume nessa tabela abaixo:

	Estatística Bayesiana	Estatística Frequentista
Dados	Fixos – Não Aleatórios	Incertos – Aleatórios
Parâmetros	Incertos – Aleatórios	Fixos – Não Aleatórios
Inferência	Incerteza sobre o valor do parâmetro	Incerteza sobre um processo de amostragem de uma população infinita
Probabilidade	Subjetiva	Objetiva (mas com diversos pressupostos dos modelos)
Incerteza	Intervalo de Credibilidade – \(P(\theta \mid y)\)	Intervalo de Confiança – \(P(y \mid \theta)\)

Vantagens da Estatística Bayesiana

Por fim, eu sumarizo as principais vantagens da estatística Bayesiana:

• Abordagem Natural para expressar incerteza
• Habilidade de incorporar informações prévia
• Maior flexibilidade do modelo
• Distribuição posterior completa dos parâmetros
  • Intervalos de Confiança vs Intervalos de Credibilidade
• Propagação natural da incerteza

E eu acredito que preciso também mostrar a principal desvantagem:

• Velocidade lenta de estimativa do modelo (30 segundos ao invés de 3 segundos na abordagem frequentista)

O começo do fim da Estatística Frequentista

Caro leitor, saiba que você está em um momento da história no qual a Estatística está passando por grandes mudanças. Acredito que a estatística frequentista, em especial a maneira que qualificamos evidências e hipóteses com \(p\)-valores se transformará de maneira “significante.” Há cinco anos atrás, a American Statistical Association (ASA, maior organização profissional de estatística do mundo) publicou uma declaração sobre \(p\)-valores (Wasserstein & Lazar, 2016). A declaração diz exatamente o que falamos aqui. Os conceitos principais do teste de significância de hipótese nula e, em particular \(p\)-valores não conseguem prover o que os pesquisadores requerem deles. Apesar do que dizem muitos livros de estatística, materiais de ensinos e artigos publicados, \(p\)-valores abaixo de 0,05 não “provam” a realidade de nada. Nem, chegando a esse ponto, os \(p\)-valores acima de 0,05 refutam alguma coisa. A declaração da ASA tem mais de 3.600 citações provocando impacto relevante. Como um exemplo, um simpósio internacional foi promovido em 2017 que originou uma edição especial de acesso aberto da The American Statistician dedicada à maneiras práticas de abandonarmos \(p < 0.05\) (Wasserstein, Schirm, & Lazar, 2019).

Logo na sequência vieram mais tentativas e reivindicações. Em setembro de 2017, a Nature Human Behaviour publicou um editorial propondo que o nível de significância do \(p\)-valor seja reduzido de \(0.05\) para \(0.005\) (Benjamin et al., 2018). Diversos autores, inclusive muitos estatísticos altamente influentes e importantes argumentaram que esse simples passo ajudaria a combater o problema da crise de replicabilidade da ciência, que muitos acreditam ser a principal consequência do uso abusivo de \(p\)-valores (Ioannidis, 2019). Além disso, muitos foram um passo além e sugerem que a ciência descarte de uma vez por todas \(p\)-valores (“It’s time to talk about ditching statistical significance,” 2019; Lakens et al., 2018). Muitos sugerem (eu inclusive) que a principal ferramenta de inferência seja a estatística Bayesiana (Amrhein, Greenland, & McShane, 2019; Goodman, 2016; van de Schoot et al., 2021)

Stan

Stan (Carpenter et al., 2017) é uma plataforma para modelagem e computação estatística de alto desempenho. Milhares de usuários contam com Stan para modelagem estatística, análise de dados e previsão nas ciências sociais, biológicas e físicas, engenharia e negócios. Stan tem mais de 3.600 citações no Google Scholar³⁰. Além disso, Stan tem o suporte financeiro da NumFOCUS, uma fundação sem fins lucrativos que dá apoio financeiro à projetos de softwares opensource. Dentre os patrocinadores da NumFOCUS podemos citar AWS Amazon, Bloomberg, Microsoft, IBM, RStudio, Facebook, NVIDIA, Netflix, entre outras.

Os modelos em Stan são especificados pela sua própria linguagem (similar à C++) e são compilados em um arquivo executável que gera inferências estatísticas Bayesiana com amostragem Monte Carlo de correntes Markov (Markov Chain Monte Carlo – MCMC) de alto desempenho. Stan possui interfaces para as seguintes linguagens de programação³¹:

• R: RStan e CmdStanR
• Python: PyStan e CmdStanPy
• Shell (Linha de Comando): CmdStan
• Julia: Stan.jl
• Scala: ScalaStan
• Matlab: MatlabStan
• Stata: StataStan
• Mathematica: MathematicaStan

Para instalar Stan o usuário deve possuir um compilador C++ no seu sistema operacional³². Essa é a principal dependência do Stan, uma vez que todas suas outras dependências (Boost e Eigen) são bibliotecas header-only e não precisam de configurações adicionais a não ser um compilador C++ funcional.

A linguagem Stan possui uma curva de aprendizagem bem desafiadora, por isso Stan possui um ecossistema de pacotes de interfaces que muitas vezes ajudam e simplificam a sua utilização:

• rstanarm: ajuda o usuário a especificar modelos usando a síntaxe familiar de fórmulas do R.
• brms: similar ao rstanarm pois usa a síntaxe familiar de fórmulas do R, mas dá maior flexibilidade na especificação de modelos mais complexos³³.

Stan³⁴ usa um amostrador MCMC que utiliza dinâmica Hamiltoniana (Hamiltonian Monte Carlo – HMC) para guiar as propostas de amostragem de novos parâmetros no sentido do gradiente da densidade de probabilidade da posterior. Isto implica em um amostrador mais eficiente e que consegue explorar todo o espaço amostral da posterior com menos iterações; e também mais eficaz que consegue tolerar diferentes geometrias de espaços amostrais da posterior. Em outras palavras, Stan usa técnicas de amostragem avançadas que permite com que modelos complexos Bayesianos atinjam convergência de maneira rápida. No Stan, raramente deve-se ajustar os parâmetros do algoritmo HMC, pois geralmente os parâmetros padrões (out-of-the-box) funcionam muito bem. Assim, o usuário foca no que é importante: a especificação dos componentes probabilísticos do seu modelo Bayesiano.

Stan é a ferramenta mais popular e poderosa de inferência Bayesiana, veja abaixo um vídeo de uma série popular chamada Billions, temporada 3 episódio 9. Interessante aqui é que não se menciona outras ferramentas extremamente populares em análise de dados³⁵ e coloca Stan no mesmo patamar que Python, Julia e C++.

História do Stan

Stan é uma homenagem ao matemático Stanislaw Ulam (figura 9), que participou do projeto Manhattan e ao tentar calcular o processo de difusão de neutrons para a bomba de hidrogênio acabou criando uma classe de métodos chamada Monte Carlo.

Figure 9: Stanislaw Ulam. Figura de https://www.wikipedia.org

Métodos de Monte Carlo possuem como conceito subjacente o uso a aleatoriedade para resolver problemas que podem ser determinísticos em princípio. Eles são freqüentemente usados em problemas físicos e matemáticos e são mais úteis quando é difícil ou impossível usar outras abordagens. Os métodos de Monte Carlo são usados principalmente em três classes de problemas: otimização, integração numérica e geração de sorteios a partir de uma distribuição de probabilidade.

A ideia do método veio enquanto jogava paciência durante sua recuperação de uma cirurgia, Ulam pensou em jogar centenas de jogos para estimar estatisticamente a probabilidade de um resultado bem-sucedido. Conforme ele mesmo menciona em Eckhardt (1987):

Os primeiros pensamentos e tentativas que fiz para praticar [o Método de Monte Carlo] foram sugeridos por uma pergunta que me ocorreu em 1946 quando eu estava convalescendo de uma doença e jogando paciência. A questão era quais são as chances de que um jogo de paciência com 52 cartas obtivesse sucesso? Depois de passar muito tempo tentando estimá-los por meio de cálculos combinatórios puros, me perguntei se um método mais prático do que o “pensamento abstrato” não seria expô-lo, digamos, cem vezes e simplesmente observar e contar o número de jogadas bem-sucedidas. Isso já era possível imaginar com o início da nova era de computadores rápidos, e eu imediatamente pensei em problemas de difusão de nêutrons e outras questões de física matemática e, de forma mais geral, como mudar os processos descritos por certas equações diferenciais em uma forma equivalente interpretável como uma sucessão de operações aleatórias. Mais tarde [em 1946], descrevi a ideia para John von Neumann e começamos a planejar cálculos reais.

Por ser secreto, o trabalho de von Neumann e Ulam exigia um codinome. Um colega de von Neumann e Ulam, Nicholas Metropolis³⁶, sugeriu usar o nome Monte Carlo, que se refere ao Casino Monte Carlo em Mônaco, onde o tio de Ulam (Michał Ulam) pedia dinheiro emprestado a parentes para jogar.

Caso o leitor se interesse na história por trás da criação do Stan veja esse vídeo abaixo do Youtube da StanCon 2018.

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
[1] tibble_3.1.2    ggplot2_3.3.3   patchwork_1.1.1 cowplot_1.1.1  

loaded via a namespace (and not attached):
 [1] bslib_0.2.5.1     compiler_4.1.0    pillar_1.6.1     
 [4] jquerylib_0.1.4   highr_0.9         tools_4.1.0      
 [7] digest_0.6.27     downlit_0.2.1     jsonlite_1.7.2   
[10] evaluate_0.14     lifecycle_1.0.0   gtable_0.3.0     
[13] pkgconfig_2.0.3   rlang_0.4.11      DBI_1.1.1        
[16] distill_1.2       yaml_2.2.1        parallel_4.1.0   
[19] xfun_0.23         withr_2.4.2       dplyr_1.0.6      
[22] stringr_1.4.0     knitr_1.33        generics_0.1.0   
[25] vctrs_0.3.8       sass_0.4.0        systemfonts_1.0.2
[28] tidyselect_1.1.1  grid_4.1.0        glue_1.4.2       
[31] R6_2.5.0          textshaping_0.3.4 fansi_0.5.0      
[34] rmarkdown_2.8     farver_2.1.0      purrr_0.3.4      
[37] magrittr_2.0.1    scales_1.1.1      htmltools_0.5.1.1
[40] ellipsis_0.3.2    assertthat_0.2.1  colorspace_2.0-1 
[43] labeling_0.4.2    ragg_1.1.2        utf8_1.2.1       
[46] stringi_1.6.2     munsell_0.5.0     crayon_1.4.1     

---

1. maiúsculo, pois se refere ao teorema de Bayes que é um sobrenome.↩︎

2. do inglês prior distribution.↩︎

3. do inglês likelihood function.↩︎

4. do inglês posterior distribution↩︎

5. pessoalmente, como um bom Popperiano, não acredito que haja ciência sem ser baseada em evidências; o que não usa evidências pode ser considerado como lógica, filosofia ou práticas sociais (não menos ou mais importantes que a ciência, apenas uma demarcação do que é ciência e do que não é; ex: matemática e direito).↩︎

6. seu smartphone (iPhone 12 - 4GB RAM) possui 1.000.000x (1 milhão) mais poder computacional que o computador de bordo da Apollo 11 (4kB RAM) que levou o homem à lua. Detalhe: esse computador de bordo era responsável pela navegação, rota e controles do módulo lunar.↩︎

7. caso o leitor queira uma discussão aprofundada veja Nau (2001).↩︎

8. do inglês sufficient statistic.↩︎

9. observação minha: relacionado à abordagem Bayesiana subjetiva.↩︎

10. observação minha: relacionado à abordagem frequentista objetiva.↩︎

11. um número que pode ser expressado como um ponto em uma linha contínua que se origina em menos infinito e termina e mais infinito \((-\infty, +\infty)\); para quem gosta de computação é um ponto flutuante float ou double.↩︎

12. na matemática axiomas são afirmações pressupostas como verdadeiras que servem como premissas or pontos de partidas para elaboração de argumentos e teoremas. Muitas vezes os axiomas são questionáveis, por exemplo geometria não-Euclidiana refuta o quinto axioma de Euclides sobre linhas paralelas. Até agora não há nenhum questionamento que tenha suportado o escrutínio do tempo e da ciência sobre os três axiomas da probabilidade.↩︎

13. por exemplo, o resultado de uma moeda dado é um dos 2 eventos mutualmente exclusivos: cara ou coroa.↩︎

14. palavra de escoteiro.↩︎

15. o nome formal do teorema é Bayes-Price-Laplace, pois Thomas Bayes foi o primeiro a descobrir, Richard Price pegou seus rascunhos, formalizou em notação matemática e apresentou para a Royal Society of London, e Pierre Laplace redescobriu o teorema sem ter tido contato prévio no final do século XVIII na França ao usar probabilidade para inferência estatística com dados do Censo na era Napoleônica.↩︎

16. vou cobrir probabilidades prévias –priori– no conteúdo da Aula 4 - Priors↩︎

17. também chamada de ortodoxa.↩︎

18. eu avisei que não era intuitivo…↩︎

19. seu “sentido aranha” deve estar disparando agora…↩︎

20. algo que vale notar: a verossimilhança também carrega muita subjetividade.↩︎

21. para os que gostam de matemática, calculamos em qual ponto de \(\theta\) a derivada da função de verossimilhança é zero – \(\mathcal{L}^\prime = 0\). Então estamos falando de um processo de otimização que para algumas funções de verossimilhança nós podemos derivar uma solução analítica.↩︎

22. eu já avisei que não é tão intuitivo?↩︎

23. seu smartphone (iPhone 12 - 4GB RAM) possui 1.000.000x (1 milhão) mais poder computacional que o computador de bordo da Apollo 11 (4kB RAM) que levou o homem à lua. Detalhe: esse computador de bordo era responsável pela navegação, rota e controles do módulo lunar.↩︎

24. isto foi copiado de Andrew Gelman – Estatístico Bayesiano.↩︎

25. do inglês credible interval.↩︎

26. do inglês: Maximum Likelihood Estimation – MLE.↩︎

27. o que não é muito raro de se ver no mundo real.↩︎

28. para os curiosos é uma mistura de duas distribuições normais ambas com desvio padrão 1, mas com médias diferentes. Para completar atribui os pesos de 60% para a distribuição com média 2 e 40% para a distribuição com média 10.↩︎

29. para ser mais preciso, estimação por máxima verossimilhança em funções não-convexas não consegue achar uma solução analítica e, se formos usar um outro procedimento iterativo de maximização, há um risco de ficarmos preso na segunda – menor – moda da distribuição.↩︎

30. conforme consulta em 14 de Março de 2021.↩︎

31. estou riscando as linguagens que não são opensource por uma questão de princípios.↩︎

32. o que ocasiona muitas frustações, mas quase todos os problemas são solucionados se o usuário seguir as instruções no repositório GitHub do Stan sobre compiladores C++.↩︎

33. e geralmente a amostragem é um pouco mais rápida que o rstanarm.↩︎

34. e consequentemente todas suas interfaces com diversas linguagens de programação e todos os pacotes do seu ecossistema.↩︎

35. nada de TensorFlow, PyTorch, Pandas, Scikit-Learn, etc…↩︎

36. também mencionado na Aula 5 - Markov Chain Montecarlo – MCMC.↩︎