Regressão Robusta Bayesiana

Modelos Lineares Generalizados – \(t\) de Student

Jose Storopoli https://scholar.google.com/citations?user=xGU7H1QAAAAJ&hl=en (UNINOVE)https://www.uninove.br
August 1, 2021

Vamos lembrar da curva Gaussiana/Normal que possui um formato de sino (figura 1). Ela não é muito alongada nas “pontas.” Ou seja, as observações não fogem muito da média. Quando usamos essa distribuição como verossimilhança na inferência modelos Bayesianos, forçamos a que todas as estimativas sejam condicionadas à uma distribuição normal da variável dependente. Se nos dados houverem muitas observações com valores discrepantes (bem diferentes da média – outliers), isso faz com que as estimativas dos coeficientes das variáveis independentes fiquem instáveis. Isso ocorre porquê a distribuição normal não consegue contemplar observações muito divergentes da média sem ter que mudar a média de posição. Em outras palavras, ela precisa se “deslocar” para conseguir estimar observações com valores discrepantes causando instabilidade da inferência.

ggplot(data = tibble(x = seq(-4, 4, length = 100))) +
  labs(
    title = "Distribuição Normais",
    subtitle = expression(list(mu == 0, sigma == 1)),
    x = expression(theta),
    y = "Densidade"
  ) +
  geom_line(aes(x, y = dnorm(x, mean = 0, sd = 1)), color = "steelblue", size = 2)
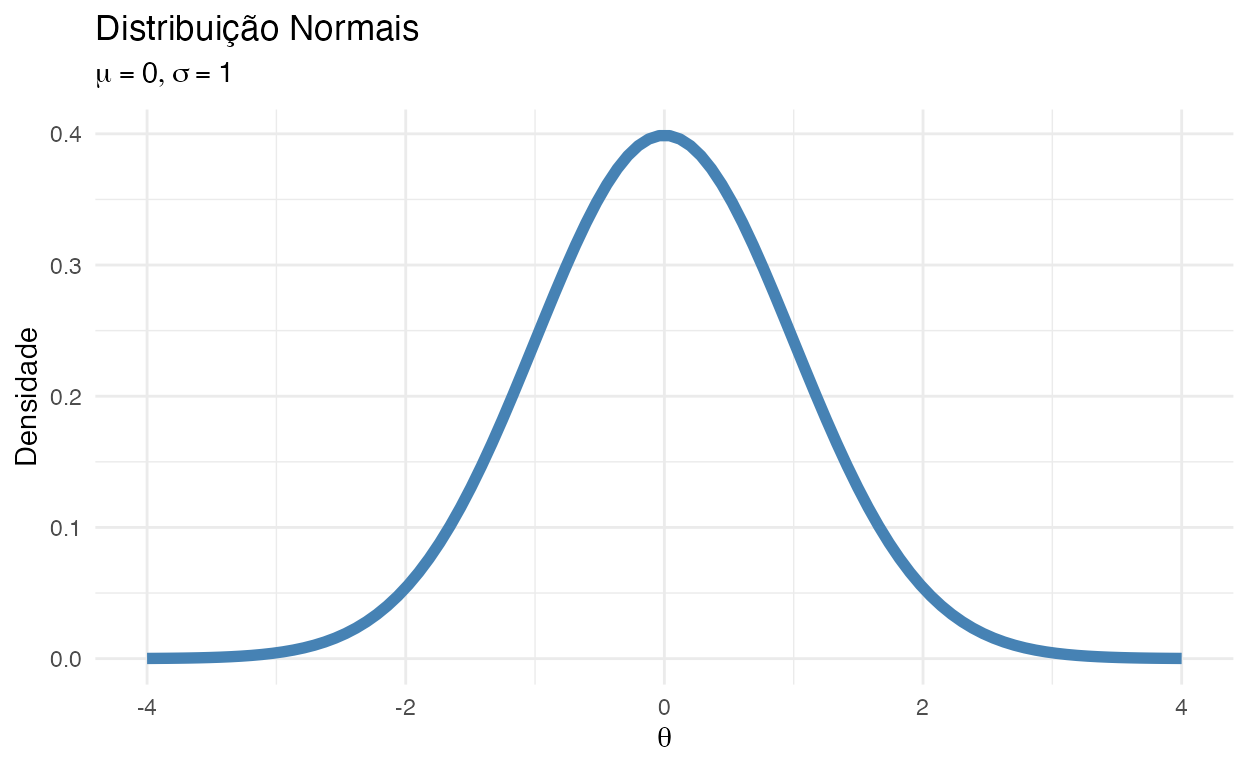
Distribuição Normal

Figure 1: Distribuição Normal

Então precisamos de uma distribuição mais “maleável” como verossimilhança. Uma distribuição que seja mais robusta à observações discrepantes (outliers). Uma distribuição similar à Normal mas que possua caudas mais longas para justamente contemplar observações muito longe da média sem ter que mudar a média de posição e ter que se “contorser” toda. Para isso temos a distribuição \(t\) de Student. Lembrando o formato dela na figura 2:

ggplot(data = tibble(x = seq(-4, 4, length = 100))) +
  labs(
    title = "Distribuição t de Student",
    subtitle = expression(list(nu == 3, mu == 0, sigma == 1)),
    x = expression(theta),
    y = "Densidade"
  ) +
  geom_line(aes(x, y = dt(x, df = 3)), color = "red", size = 2)
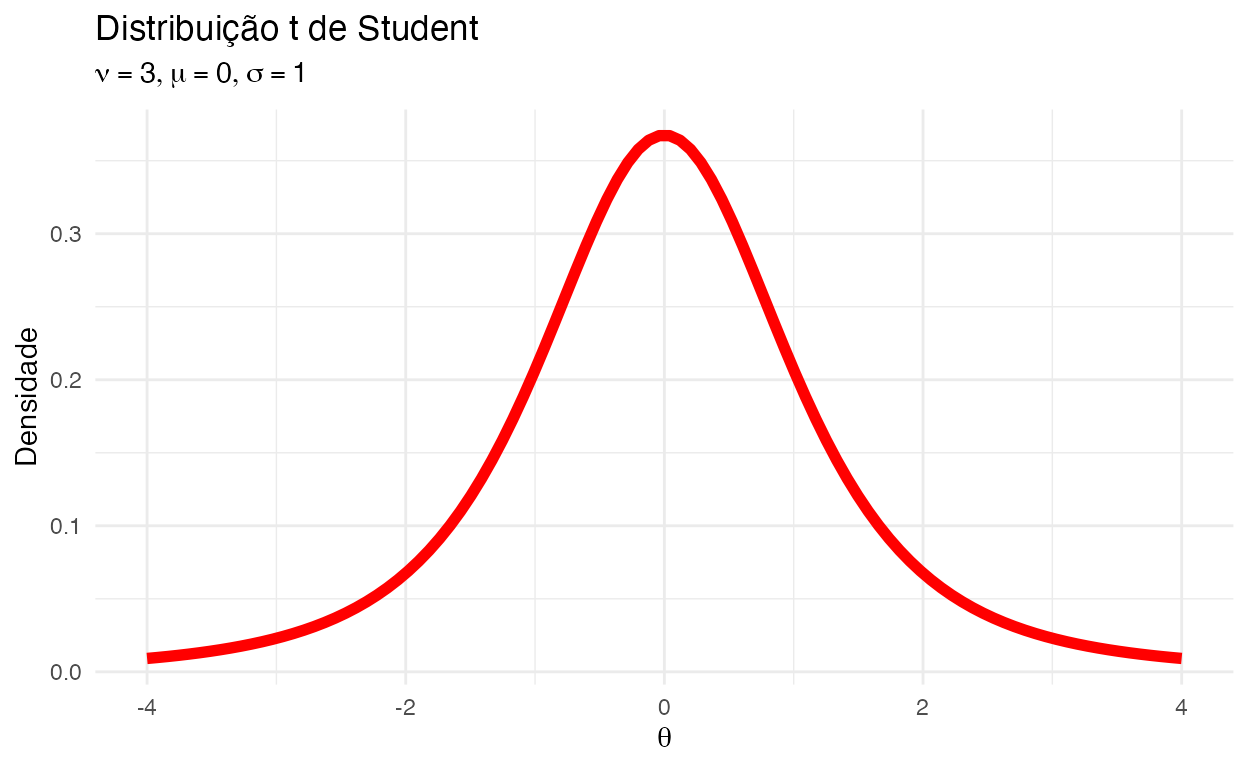
Distribuição $t$ de Student

Figure 2: Distribuição \(t\) de Student

Comparativo Normal vs Student

Reparem nas caudas na figura 3:

ggplot(data = tibble(x = seq(-4, 4, length = 100))) +
  labs(
    title = "Comparativo Distribuições Normal vs t de Student",
    subtitle = expression(list(nu == 3, mu == 0, sigma == 1)),
    x = expression(theta),
    y = "Densidade"
  ) +
  geom_line(aes(x, y = dnorm(x, mean = 0, sd = 1), color = "Normal"), size = 2) +
  geom_line(aes(x, y = dt(x, df = 3), color = "Student"), size = 2) +
  scale_color_manual(
    name = "Distribuições",
    values = c("steelblue", "red")
  )
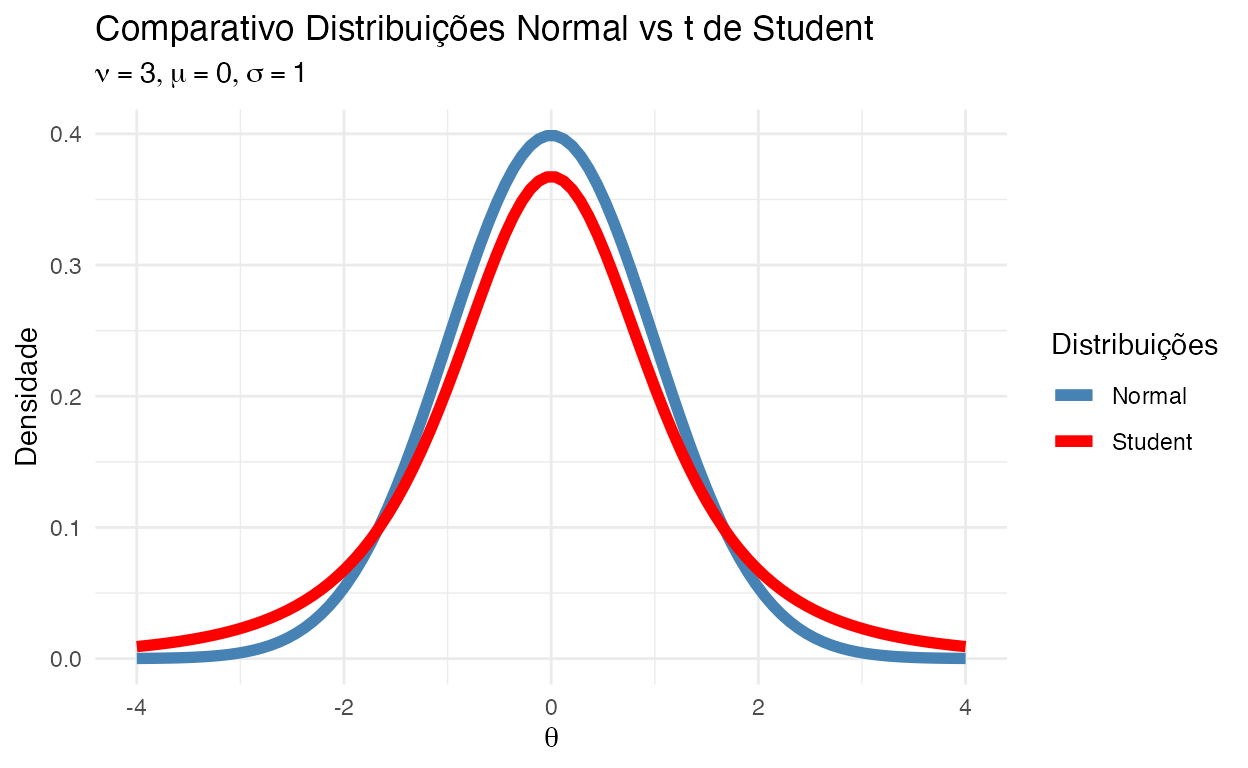
Comparativo Distribuições Normal vs $t$ de Student

Figure 3: Comparativo Distribuições Normal vs \(t\) de Student

Regressão Robusta Bayesiana

A abordagem padrão para modelarmos uma variável dependente contínua é com um função de verossimilhança Gaussiana/Normal. Isto implica que o erro do modelo, \(\sigma\) da função de verossimilhança Gaussiana/Normal seja distribuído como uma distribuição normal:

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Normal}\left( \alpha + \mathbf{X} \boldsymbol{\beta}, \sigma \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \\ \sigma &\sim \text{Exponencial}(\lambda_\sigma) \end{aligned} \]

Do ponto de vista Bayesiano, não há nada especial na verossimilhança Gaussiana/Normal. É apenas uma distribuição probabilística especificada em um modelo. Podemos deixar o modelo mais robusto ao usarmos uma distribuição \(t\) de Student como função de verossimilhança. Isto implica que o erro do modelo, \(\sigma\) não segue uma distribuição normal, mas sim uma distribuição \(t\) de Student:

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Student}\left( \nu, \alpha + \mathbf{X} \boldsymbol{\beta}, \sigma \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \\ \nu &\sim \text{Log-Normal}(2, 1) \\ \sigma &\sim \text{Exponencial}(\lambda_\sigma) \end{aligned} \]

Aqui temos algumas diferenças:

  1. A função de verossimilhança \(t\) de Student requer 1 parâmetro adicional: \(\nu\), os graus de liberdade. Esses controlam o quão “longas” serão as caudas. Valores \(\nu > 20\) fazem a distribuição \(t\) de Student praticamente se tornar uma distribuição normal.
  2. Não há nada especial em \(\nu\). É apenas mais um parâmetro para o modelo estimar. Então é só eluciar uma priori. No caso, estou usando uma Distribuição Log-Normal com média 2 e desvio padrão 1.

Veja que não há nada de especial também nas prioris dos coeficientes \(\boldsymbol{\beta}\) ou da constante \(\alpha\). Poderíamos muito bem também colocar outras distribuições ou até deixar o modelo mais robustos ainda à outliers colocando prioris \(t\) de Student:

\[ \begin{aligned} \alpha &\sim \text{Student}(\nu_\alpha, \mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Student}(\nu_{\boldsymbol{\beta}}, \mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \\ \nu_\alpha &\sim \text{Log-Normal}(1, 1) \\ \nu_{\boldsymbol{\beta}} &\sim \text{Log-Normal}(1, 1) \end{aligned} \]

Modelos Lineares Robustos com o pacote brms

O rstanarm não nos dá a possibilidade de usar distribuições \(t\) de Student como função de verossimilhança de modelos Bayesiano. Para usarmos distribuições \(t\) de Student, precisamos usar o brms (Bürkner, 2017). O brms usa a mesma síntaxe que o rstanarm e possui as mesmas famílias de funções de verossimilhança, mas com algumas diferenças:

A função que usamose para designar modelos Bayesianos no brms é a brm():

brm(y ~ ...,
    data = ...,
    family = student)

Exemplo - Prestígio de Duncan (1961)

Para exemplicar regressão robusta vamos usar um dataset que tem muitas observações discrepantes (outliers) chamado Duncan (Duncan, 1961). Ele possui 45 observações sobre ocupações nos EUA e 5 variáveis:

Como sempre eu gosto de usar o pacote skimr (Waring et al., 2021) com a função skim():

library(skimr)
duncan <- read_csv2("datasets/Duncan.csv", col_types = "ffiii")
skim(duncan)
Table 1: Data summary
Name duncan
Number of rows 45
Number of columns 5
_______________________
Column type frequency:
factor 2
numeric 3
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
profession 0 1 FALSE 45 acc: 1, pil: 1, arc: 1, aut: 1
type 0 1 FALSE 3 bc: 21, pro: 18, wc: 6

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
income 0 1 42 24 7 21 42 64 81 ▇▂▅▃▅
education 0 1 53 30 7 26 45 84 100 ▆▆▃▂▇
prestige 0 1 48 32 3 16 41 81 97 ▇▃▅▂▇

Eu acho que variável dependente prestige merece uma atenção maior, vejam o histograma dela na figura 4. Parece que temos uma multimodalidade rolando por aqui:

ggplot(duncan, aes(prestige)) +
  geom_histogram(bins = 15, fill = "steelblue") +
  labs(
    title = "Histograma da variável prestige",
    y = "Frequência"
  )
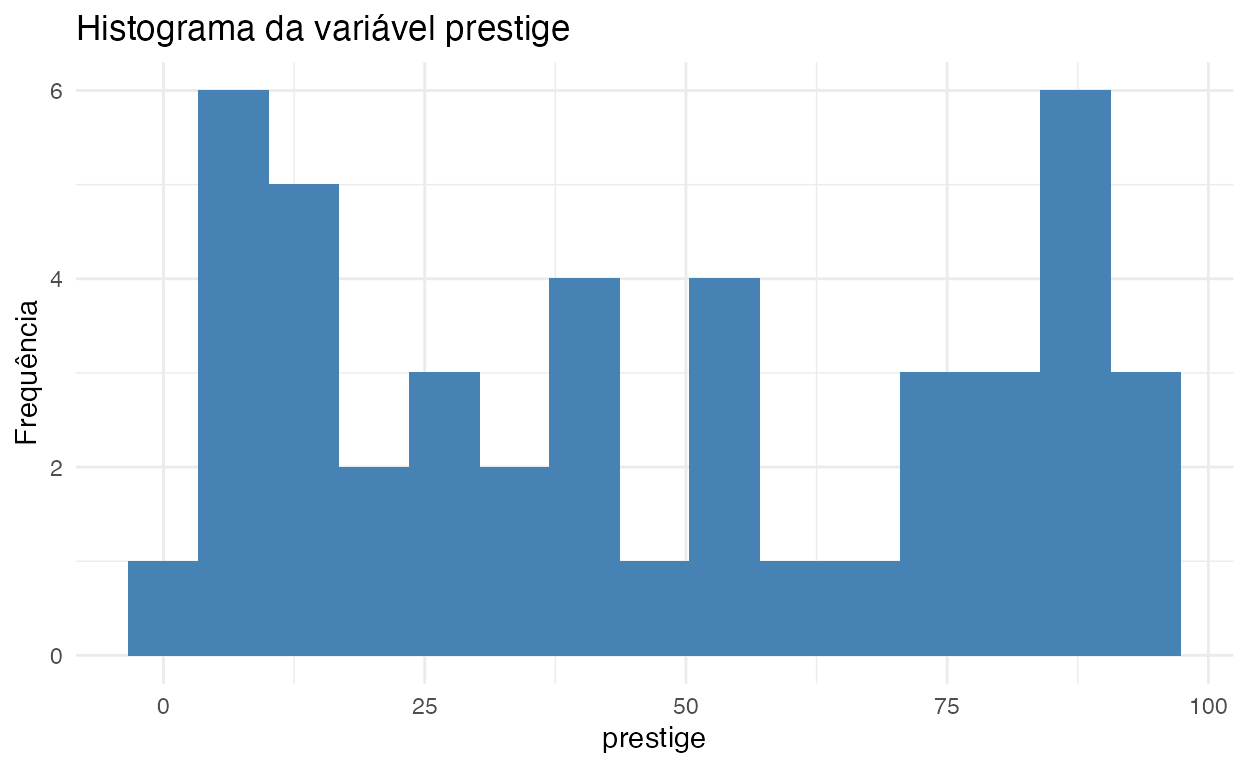
Histograma da variável `prestige`

Figure 4: Histograma da variável prestige

Primeiro modelo: Regressão Linear

Vamos estimar primeiramente uma regressão linear usando a distribuição Normal como verossimilhança no rstanarm. Para exemplificação vou manter as prioris padrões do rstanarm:

# Detectar quantos cores/processadores
options(mc.cores = parallel::detectCores())
options(Ncpus = parallel::detectCores())

library(rstanarm)

model_1 <- stan_glm(
  prestige ~ income + education,
  data = duncan,
  family = gaussian # nem precisaria pois é o argumento padrão
)

E na sequência o sumário das estimativas do modelo, assim como os diagnósticos da MCMC:

summary(model_1)


Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      prestige ~ income + education
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 45
 predictors:   3

Estimates:
              mean   sd    10%   50%   90%
(Intercept)  -6.1    4.6 -12.0  -6.2  -0.2
income        0.6    0.1   0.4   0.6   0.8
education     0.5    0.1   0.4   0.5   0.7
sigma        13.8    1.6  11.8  13.6  15.8

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 47.6    2.9 43.9  47.7  51.3 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.1  1.0  4499 
income        0.0  1.0  2089 
education     0.0  1.0  2319 
sigma         0.0  1.0  1977 
mean_PPD      0.1  1.0  3023 
log-posterior 0.0  1.0  1343 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Aparentemente parece que o modelo possui boas métricas (todos Rhat menores que 1.01) mas quando olhamos o Posterior Predictive Check (figura 5), vemos uma bagunça:

pp_check(model_1, nreps = 40)
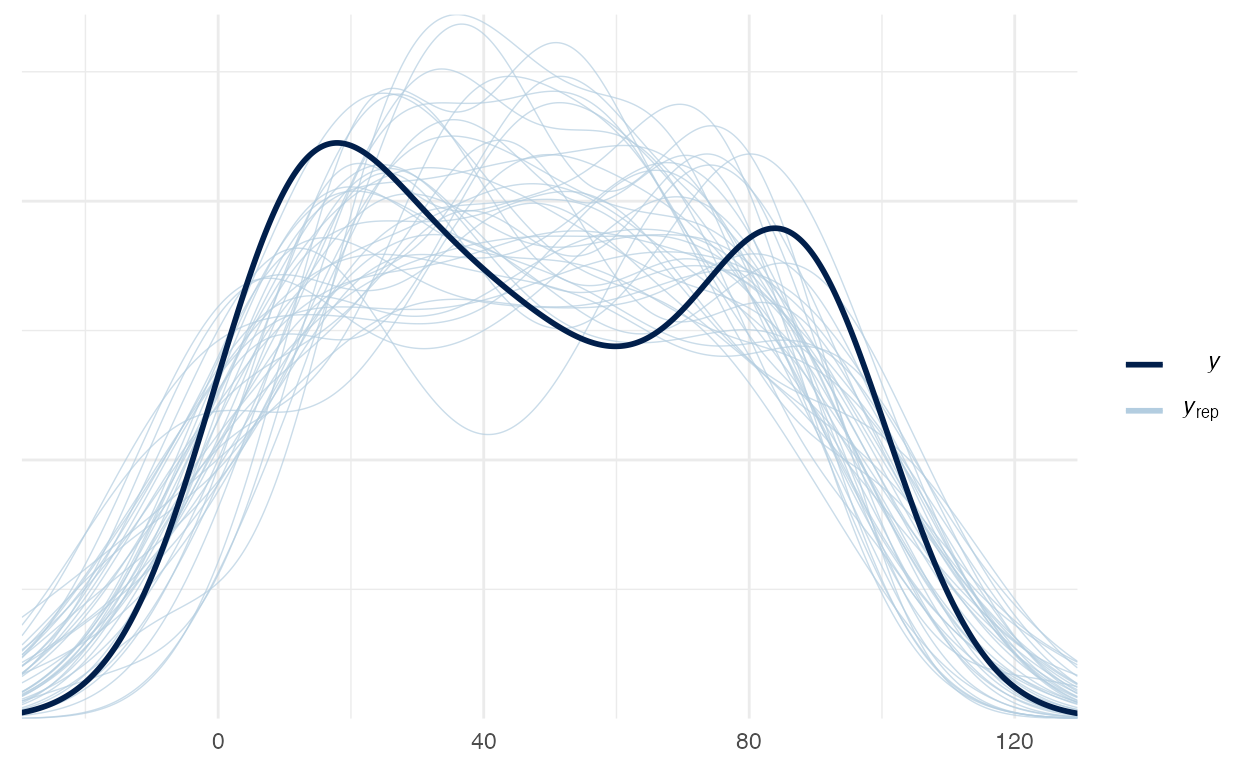
*Posterior Preditive Check* do modelo Gaussiano/Normal

Figure 5: Posterior Preditive Check do modelo Gaussiano/Normal

Segundo modelo: Regressão Robusta

Para rodar um modelo Bayesiano que usa como verossimilhança a distribuição \(t\) de Student basta somente usar a mesma síntaxe que o stan_glm mas colocando argumento family = student. Aqui vou usar as mesmas priors que o padrão do rstanarm (caso queira, é só verificá-las com o prior_summary(model_1)):

library(brms)
model_2 <- brm(
  prestige ~ income + education,
  data = duncan,
  family = student,
  prior = c(
    prior(normal(0, 3.22), class = b, coef = income),
    prior(normal(0, 2.65), class = b, coef = education),
    prior(normal(48, 79), class = Intercept),
    prior(exponential(0.032), class = sigma),
    prior(lognormal(2, 1), class = nu)
  )
)

E na sequência o sumário das estimativas do modelo com verossimilhança \(t\) de Student (estou colocando o prob = 0.9 para que o sumário do modelo brms seja o mesmo que o sumário do rstanarm), assim como os diagnósticos da MCMC:

summary(model_2, prob =  0.9)

 Family: student 
  Links: mu = identity; sigma = identity; nu = identity 
Formula: prestige ~ income + education 
   Data: duncan (Number of observations: 45) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Population-Level Effects: 
          Estimate Est.Error l-90% CI u-90% CI Rhat Bulk_ESS Tail_ESS
Intercept    -7.03      3.91   -13.29    -0.40 1.00     4796     3249
income        0.69      0.14     0.46     0.91 1.00     1582     2198
education     0.49      0.11     0.32     0.67 1.00     1615     2057

Family Specific Parameters: 
      Estimate Est.Error l-90% CI u-90% CI Rhat Bulk_ESS Tail_ESS
sigma    11.27      2.13     7.67    14.72 1.00     1383     1501
nu       10.70     12.35     2.09    33.90 1.00     1676     1549

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Vemos que o erro do modelo sigma reduziu de \(\approx 14\) para \(\approx 11\), o que implica em uma melhor inferência do modelo. Além disso, temos um novo parâmetro estimado pelo modelo que é o parâmetro nu (\(\nu\)): os graus de liberdade da distribuição \(t\) de Student usada como verossimilhança.

E para concluir, vejam que p Posterior Predictive Check (figura 6) ficou com um aspecto muito melhor que o modelo linear:

pp_check(model_2, nsamples = 40)
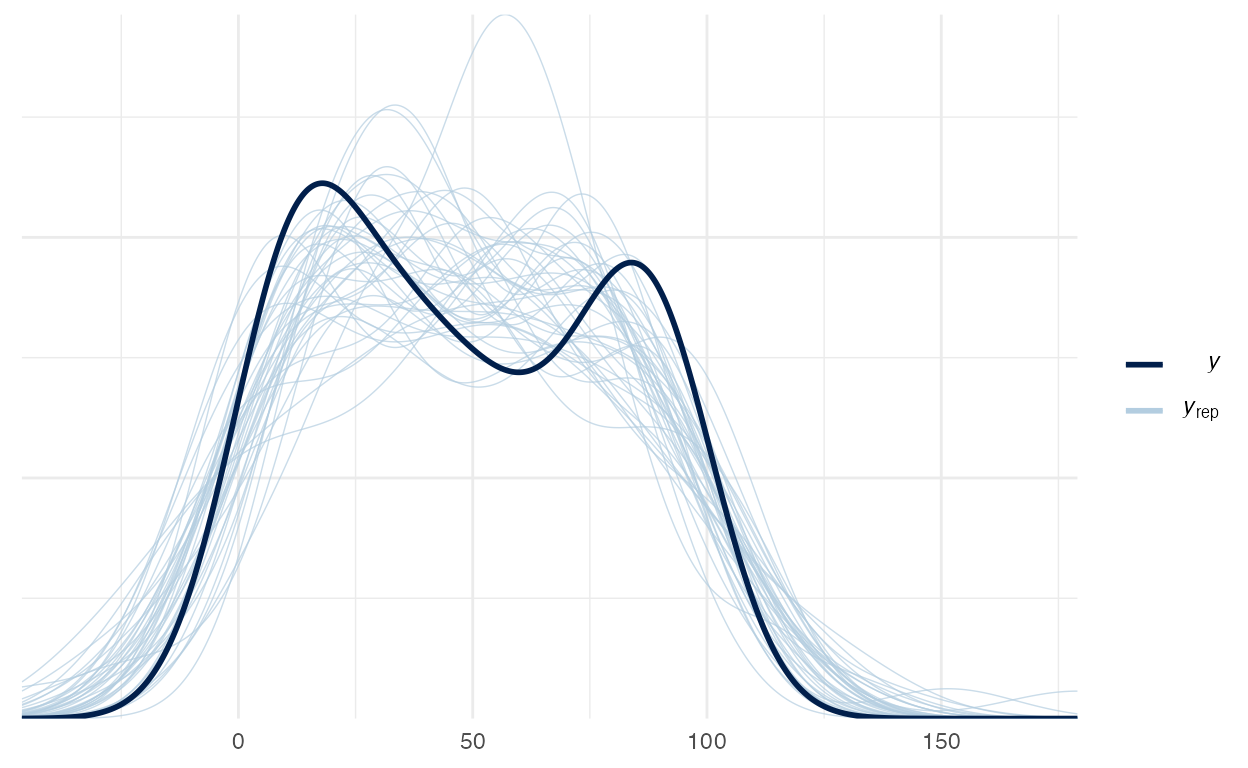
*Posterior Preditive Check* do modelo $t$ de Student

Figure 6: Posterior Preditive Check do modelo \(t\) de Student

Atividade Prática

O dataset Boston Housing está disponível em datasets/Boston_Housing.csv. Possui 506 observações e possui 14 variáveis:

###

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] gapminder_0.3.0      ggExtra_0.9          dplyr_1.0.6         
 [4] rstan_2.21.2         StanHeaders_2.21.0-7 MASS_7.3-54         
 [7] ggforce_0.3.3        gganimate_1.0.7      plotly_4.9.3        
[10] carData_3.0-4        DiagrammeR_1.0.6.1   brms_2.15.0         
[13] rstanarm_2.21.1      Rcpp_1.0.6           skimr_2.1.3         
[16] readr_1.4.0          readxl_1.3.1         tibble_3.1.2        
[19] ggplot2_3.3.3        patchwork_1.1.1      cowplot_1.1.1       

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         lazyeval_0.2.2       repr_1.1.3          
  [7] splines_4.1.0        crosstalk_1.1.1      rstantools_2.1.1    
 [10] inline_0.3.19        digest_0.6.27        htmltools_0.5.1.1   
 [13] magick_2.7.2         rsconnect_0.8.18     fansi_0.5.0         
 [16] magrittr_2.0.1       RcppParallel_5.1.4   matrixStats_0.59.0  
 [19] xts_0.12.1           prettyunits_1.1.1    colorspace_2.0-1    
 [22] textshaping_0.3.4    xfun_0.23            callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] polyclip_1.10-0      gtable_0.3.0         V8_3.4.2            
 [34] pkgbuild_1.2.0       abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] isoband_0.2.4        progress_1.2.2       viridisLite_0.4.0   
 [43] xtable_1.8-4         tmvnsim_1.0-2        stats4_4.1.0        
 [46] DT_0.18              httr_1.4.2           htmlwidgets_1.5.3   
 [49] threejs_0.3.3        RColorBrewer_1.1-2   ellipsis_0.3.2      
 [52] pkgconfig_2.0.3      loo_2.4.1            farver_2.1.0        
 [55] sass_0.4.0           here_1.0.1           utf8_1.2.1          
 [58] tidyselect_1.1.1     labeling_0.4.2       rlang_0.4.11        
 [61] reshape2_1.4.4       later_1.2.0          visNetwork_2.0.9    
 [64] munsell_0.5.0        cellranger_1.1.0     tools_4.1.0         
 [67] cli_2.5.0            generics_0.1.0       gifski_1.4.3-1      
 [70] ggridges_0.5.3       evaluate_0.14        stringr_1.4.0       
 [73] fastmap_1.1.0        yaml_2.2.1           ragg_1.1.2          
 [76] processx_3.5.2       knitr_1.33           purrr_0.3.4         
 [79] nlme_3.1-152         mime_0.10            projpred_2.0.2      
 [82] xml2_1.3.2           compiler_4.1.0       bayesplot_1.8.0     
 [85] shinythemes_1.2.0    rstudioapi_0.13      curl_4.3.1          
 [88] gamm4_0.2-6          png_0.1-7            tweenr_1.0.2        
 [91] bslib_0.2.5.1        stringi_1.6.2        highr_0.9           
 [94] ps_1.6.0             Brobdingnag_1.2-6    lattice_0.20-44     
 [97] Matrix_1.3-3         nloptr_1.2.2.2       markdown_1.1        
[100] shinyjs_2.0.0        vctrs_0.3.8          pillar_1.6.1        
[103] lifecycle_1.0.0      jquerylib_0.1.4      bridgesampling_1.1-2
[106] data.table_1.14.0    httpuv_1.6.1         R6_2.5.0            
[109] bookdown_0.22        promises_1.2.0.1     gridExtra_2.3       
[112] codetools_0.2-18     distill_1.2          boot_1.3-28         
[115] colourpicker_1.1.0   gtools_3.8.2         assertthat_0.2.1    
[118] rprojroot_2.0.2      withr_2.4.2          mnormt_2.0.2        
[121] shinystan_2.5.0      mgcv_1.8-35          parallel_4.1.0      
[124] hms_1.1.0            grid_4.1.0           tidyr_1.1.3         
[127] coda_0.19-4          minqa_1.2.4          rmarkdown_2.8       
[130] downlit_0.2.1        shiny_1.6.0          lubridate_1.7.10    
[133] base64enc_0.1-3      dygraphs_1.1.1.6
Bürkner, P.-C. (2017). brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software, 80(1), 1–28. https://doi.org/10.18637/jss.v080.i01
Duncan, O. D. (1961). A socioeconomic index for all occupations. Class: Critical Concepts, 1, 388–426.
Waring, E., Quinn, M., McNamara, A., Arino de la Rubia, E., Zhu, H., & Ellis, S. (2021). Skimr: Compact and flexible summaries of data. Retrieved from https://CRAN.R-project.org/package=skimr

References

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY-SA 4.0. Source code is available at https://github.com/storopoli/Estatistica-Bayesiana, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Storopoli (2021, Aug. 1). Estatística Bayesiana com R e Stan: Regressão Robusta Bayesiana. Retrieved from https://storopoli.github.io/Estatistica-Bayesiana/9-Regressao_Robusta.html

BibTeX citation

@misc{storopoli2021regressaorosbustabayesR,
  author = {Storopoli, Jose},
  title = {Estatística Bayesiana com R e Stan: Regressão Robusta Bayesiana},
  url = {https://storopoli.github.io/Estatistica-Bayesiana/9-Regressao_Robusta.html},
  year = {2021}
}

© Copyright 2021 Jose Storopoli.

Content licensed under the CC BY-SA 4.0.