Estatística Bayesiana com R e Stan: Modelos Multiníveis Bayesianos

Jose Storopoli

Modelos hierárquicos Bayesianos (também chamados de modelos multiníveis) são um modelo estatístico escrito em níveis múltiplos (forma hierárquica) que estima os parâmetros da distribuição posterior usando a abordagem Bayesiana. Os submodelos se combinam para formar o modelo hierárquico, e o teorema de Bayes é usado para integrá-los aos dados observados e contabilizar toda a incerteza que está presente. O resultado dessa integração é a distribuição posterior, também conhecida como estimativa de probabilidade atualizada, à medida que evidências adicionais da função de verossimilhança são integradas juntamente com a distribuição priori dos parâmetros.

A modelagem hierárquica é usada quando as informações estão disponíveis em vários níveis diferentes de unidades de observação. A forma hierárquica de análise e organização auxilia no entendimento de problemas multiparâmetros e também desempenha um papel importante no desenvolvimento de estratégias computacionais.

Os modelos hierárquicos são descrições matemáticas que envolvem vários parâmetros, de modo que as estimativas de alguns parâmetros dependem significativamente dos valores de outros parâmetros. A figura 1 mostra um modelo hierárquico no qual há um hiperparamêtro $\phi$ que parametriza os parâmetros $\theta_1, \theta_2, \dots, \theta_N$ que por fim são usados para inferir a densidade posterior de alguma variável de interesse $\mathbf{y} = y_1, y_2, \dots, y_N$.

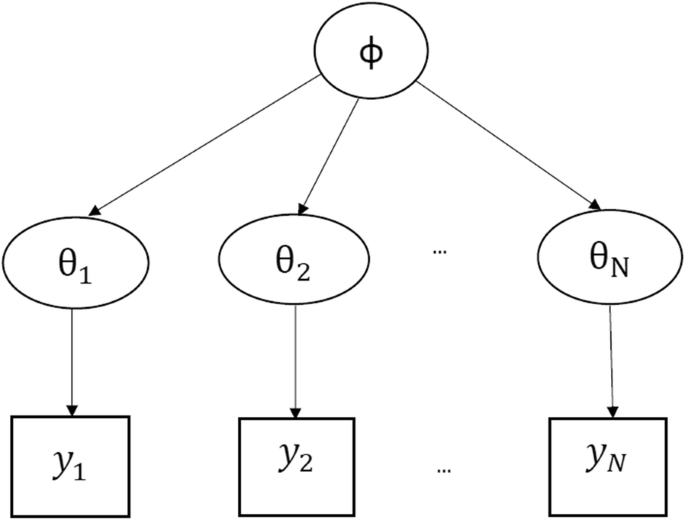
Figure 1: Modelo Hierárquico

Quando usar Modelos Multiníveis?

Modelos multiníveis são particularmente apropriados para projetos de pesquisa onde os dados dos participantes são organizados em mais de um nível (ou seja, dados aninhados – nested data). As unidades de análise geralmente são indivíduos (em um nível inferior) que estão aninhados em unidades contextuais/agregadas (em um nível superior). Um exemplo é quando estamos mensurando desempenho de indivíduos e temos informações adicionais sobre pertencimento à grupos distintos como sexo, faixa etária, nível hierárquico, nível educacional ou estado/província de residência.

Há um pressuposto principal que não pode ser violado em modelos multiníveis que é o de permutabilidade¹ (de Finetti, 1974; Nau, 2001). Sim, esse é o mesmo pressuposto que discutimos na Aula 0 - O que é Estatística Bayesiana. Esse pressuposto parte do princípio que os grupos são permutáveis. A figura 2 mostra uma representação gráfica da permutabilidade. Os grupos mostrados como “copos” que contém observações mostradas como “bolas.” Se esse pressuposto é violado na sua inferência, então modelos multiníveis não são apropriados. Isto quer dizer que, uma vez que não há justificação teórica para sustentar a permutabilidade, as inferências do modelo multinível não são robustas e o modelo pode sofrer de diversas patologias e não deve ser usado para qualquer análise científica ou prática.

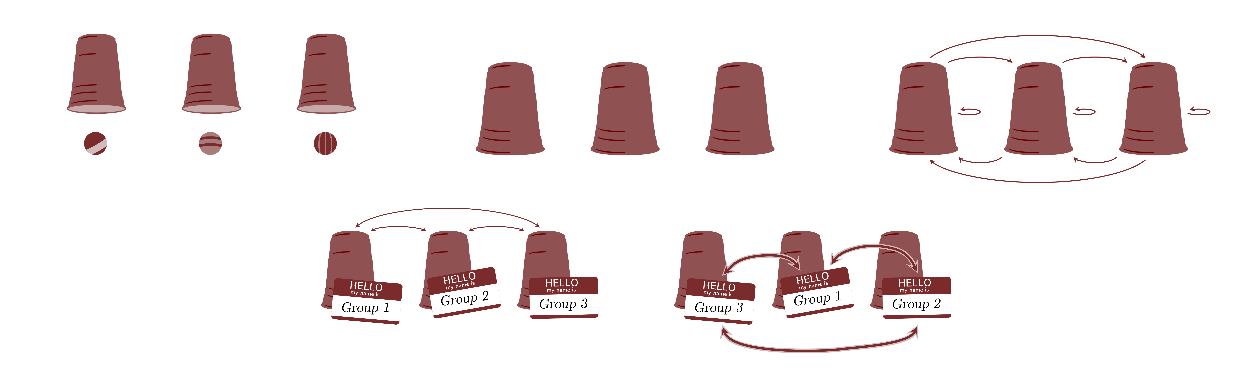
Figure 2: Permutabilidade – Figuras de Michael Betancourt – https://betanalpha.github.io/

Hiperpriori (Hyperprior)

Como as prioris dos parâmetros são amostradas de uma outra priori do hiperparâmetro (parâmetro do nível superior), as prioris do nível superior são chamadas de hiperprioris (do inglês hyperprior). Isso faz com que estimativas de um grupo ajudem o modelo a estimar melhor os outros grupos proporcionando estimativas mais robustas e estáveis.

Chamamos os parâmetros globais de efeitos populacionais (population-level effects, também às vezes chamados de efeitos fixos, fixed effects) e os parâmetros de cada grupo de efeitos de grupo (group-level effects, também às vezes chamados de efeitos aleatórios, random effects). Por isso que os modelos multiníveis são conhecidos também como modelos mistos (mixed models) no qual temos efeitos fixos e efeitos aleatórios.

Abordagem Frequentista vs Abordagem Bayesiana

Existem modelos multíveis também na estatística frequentista. Todos esses estão disponíveis no pacote lme4 (Bates, Mächler, Bolker, & Walker, 2015). rstanarm e brms usam a mesma síntaxe de fórmula do lme4 para especificar parâmetros populacionais e parâmetros de grupo. Mas aqui há uma grande diferença da abordagem frequentista vs a abordagem Bayesiana.

Primeiro, a abordagem frequentista (como já cobrimos na Aula 0 - O que é Estatística Bayesiana) usa um procedimento de otimização da função de verossimilhança na qual busca-se o conjunto de parâmetros que maximizam a função de verossimilhança do modelo. Na prática isso significa achar a moda de todos os parâmetros condicionados na função de verossimilhança que, pelo pressuposto de que todos os parâmetros são distribuídos como uma distribuição normal e também por conta do pressuposto de erros gaussianos, equivale à média e à mediana do parâmetro (note que na distribuição normal média, mediana e moda possuem o mesmo valor). Procure em fóruns de estatística ou no stackoverflow e você achará um monte de perguntas e pedidos de ajuda sobre modelos multiníveis lme4 que não convergem. Aliás, muitos são convencidos para a abordagem Bayesiana (e se tornam Bayesianos) quando eles tentam executar o mesmo modelo lme4 que falhou a convergência no rstanarm ou brms (lembrando que a síntaxe da fórmula é a mesma, então é muito fácil traduzir modelos frequentistas do lme4 para modelos bayesianos do rstanarm e brms) e o modelo converge na sua primeira tentativa.

Segundo, na abordagem frequentista, modelos multiníveis não computam $p$-valores dos efeitos de grupo (veja a explicação aqui do Douglas Bates autor do pacote lme4). Por conta da contorção matemática de diversas aproximações que a estatística frequentista tem que fazer (na sua determinação cega de não usar o teorema de Bayes pois conjecturas probabilísticas dos parâmetros são proibidas), o cálculo de $p$-valores de efeitos de grupo possuem fortes pressupostos. O principal é que os grupos são balanceados. Ou seja, os grupos são homogêneos no seu tamanho. Qualquer desbalanço na composição dos grupos (um grupo com mais observações que outros) resulta em $p$-valores patológicos e que não podem ser confiáveis.

Sumarizando, a abordagem frequentista para modelos multiníveis não é robusta tanto no processo da inferência (falhas de convergência da estimação de máxima verossimilhança), quanto nos resultados dessa inferência (não computa $p$-valores por conta de fortes pressupostos que quase sempre são violados).

Três abordagens de Modelos Multiníveis

Modelos multiníveis geralmente se dividem em três abordagens:

Random-intercept model: Modelo no qual cada grupo recebe uma constante (intercept) diferente além da constante global e coeficientes globais
Random-slope model: Modelo no qual cada grupo recebe um coeficiente (slope) diferente para cada variável independente além da constante global
Random-intercept-slope model: Modelo no qual cada grupo recebe tanto uma constante (intercept) quanto um coeficiente (slope) diferente para cada variável independente além da constante global

rstanarm e brms possuem as funcionalidades completas para rodar modelos multiníveis e a única coisa a se fazer é alterar a fórmula. Para rstanarm, há uma segunda mudança também que não usamos mais a função stan_glm() mas sim a função stan_glmer(). Para brms não há mudança e usamos a mesma função brm().

Random-Intercept Model

A primeira abordagem é o random-intercept model na qual especificamos para cada grupo uma constante diferente, além da constante global. Essas constantes são amostradas de uma hiperpriori.

No caso de random-intercept model, a fórmula a ser usada segue este padrão:

y ~ (1 | group) + x1 + x2

O (1 | group) na fórmula sinaliza que a constante 1 deve ser também especificada para cada um dos grupos listados nos valores da variável group (aqui você substitui group por qualquer variável que quiser). Na prática essa fórmula, tanto no rstanarm quanto no brms é expandida para:

y ~ 1 + (1 | group) + x1 + x2

Isto indica que há uma constante global (nível populacional) e também uma constante para cada grupo. Caso queira remover do modelo a constante global (algo que eu recomendo apenas se tiver muita fundamentação teórica para tal manobra) é só especificar o 0 como constante global. Isto sinaliza que o modelo possui apenas constantes para cada grupo e que não há uma constante global a ser estimada:

y ~ 0 + (1 | group) + x1 + x2

Além disso você pode especificar uma constante para quantos grupos quiser. É só adicioná-los na fórmula:

y ~ (1 | group1) + (1 | group2) + x1 + x2

Random-Slope Model

A segunda abordagem é o random-slope model na qual especificamos para cada grupo um coeficiente diferente para cada variável independente desejada, além da constante global. Esses coeficientes são amostrados de uma hiperpriori.

No caso de random-slope model, a formula a ser usada segue este padrão. Ela indica que o coeficiente da variável independente deve ser estimado de maneira local com coeficientes para cada grupo. Note que usamos o 0 pois neste caso sinalizamos que apenas a variável independente deve possuir coeficientes para cada grupo e não a constante:

y ~ (0 + x1 | group) + (0 + x2 | group)

Note que para rstanarm e brms a fórmula se transforma em:

y ~ 1 + (0 + x1 | group) + (0 + x2 | group)

Indicando que há uma constante global e coeficientes de grupo (local) para as variáveis independentes.

Random-Intercept-Slope Model

A terceira abordagem é o random-intercept-slope model na qual especificamos para cada grupo uma constante (intercept) diferente juntamente com coeficientes (slope) diferentes para cada variável independente desejada. É claro também resulta em uma costante global. Essas constantes e coeficientes à nível de grupo são amostrados de duas ou mais hiperprioris.

No caso de random-intercept-slope model, a formula a ser usada segue este padrão:

y ~ (1 + x1 | group) + (1 + x2 | group)

Note novamente que para rstanarm e brms a fórmula se transforma em:

y ~ 1 + (1 + x1 | group) + (1 + x2 | group)

Prioris de Modelos Multiníveis

Antes de nos aventurarmos em estimar modelos, vamos relembrar as prioris da da Aula 4 - Priors:

Argumento	Usado em	Aplica-se à
`prior_intercept`	Todas funções de modelagem exceto `stan_polr` and `stan_nlmer`	Constante (intercept) do modelo, após centralização dos preditores
`prior`	Todas funções de modelagem	Coeficientes de Regressão, não inclui coeficientes que variam por grupo em modelos multiníveis (veja `prior_covariance`)
`prior_aux`	`stan_glm`, `stan_glmer`, `stan_gamm4`, `stan_nlmer`	Parâmetro auxiliar (ex: desvio padrão (standard error - DP), interpretação depende do modelo
`prior_covariance`	`stan_glmer`, `stan_gamm4`, `stan_nlmer`	Matrizes de covariância em modelos multiníveis

Em especial, foquem no prior_covariance que é a priori matriz de covariância em modelos multiníveis.

Os modelos hierárquicos geralmente são especificados assim. Temos $N$ observações organizadas em $J$ grupos com $K$ variáveis independentes. O truque aqui é que inserimos uma coluna de $1$ na matrix de dados $\mathbf{X}$. Matematicamente isto se comporta como se esta coluna fosse uma variável de identidade (pois o número $1$ na operação de multiplicação $1 \cdot \beta$ é o elemento identidade. Ele mapeia $x \to x$ mantendo o valor de $x$) e, consequentemente, podemos interpretar o coeficiente dessa coluna como a constante do modelo².

Então temos os dados como uma matriz:

\[ \mathbf{X} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1K} \\ 1 & x_{21} & x_{22} & \cdots & x_{2K} \\ \vdots & \cdots & \cdots & \ddots & \vdots \\ 1 & x_{N1} & x_{N2} & \cdots & x_{NK} \end{bmatrix} \]

Assim nosso modelo (aqui representado com uma função de verossimilhança Gaussiana/Normal) fica:

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Normal}(\alpha + \mathbf{X} \boldsymbol{\beta}_{j}, \sigma) \\ \boldsymbol{\beta}_j &\sim \text{Normal Multivariada}(\boldsymbol{\mu}_j, \boldsymbol{\Sigma}) \quad \text{para}\quad j \in \{ 1, \dots, J \} \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \sigma &\sim \text{Exponencial}(\lambda_\sigma) \end{aligned} \]

Cada vetor de coeficientes $\boldsymbol{\beta}_j$ representa os coeficientes das colunas de $\mathbf{X}$ para cada grupo $j \in J$. Lembre-se que a primeira coluna de $\mathbf{X}$ é um monte de $1$, então $\beta_{j1}$ é a constante para cada grupo. Junte isso com o que já vimos em aulas anteriores sobre $\alpha$ e $\sigma$ e temos um modelo multinível para um conjunto de grupos $J$.

Caso queira mais grupos é só adicioná-los ao modelo como $J_1, J_2, \dots$:

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Normal}(\alpha + \mathbf{X} \boldsymbol{\beta}_{j1} + \mathbf{X} \boldsymbol{\beta}_{j2}, \sigma) \\ \boldsymbol{\beta}_{j1} &\sim \text{Normal Multivariada}(\boldsymbol{\mu}_{j1}, \boldsymbol{\Sigma}_1) \quad \text{para}\quad j_1 \in \{ 1, \dots, J_1 \} \\ \boldsymbol{\beta}_{j2} &\sim \text{Normal Multivariada}(\boldsymbol{\mu}_{j2}, \boldsymbol{\Sigma}_2) \quad \text{para}\quad j_2 \in \{ 1, \dots, J_2 \} \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \sigma &\sim \text{Exponencial}(\lambda_\sigma) \end{aligned} \]

Podemos especificar uma priori para a matriz de covariância $\boldsymbol{\Sigma}$ no rstanarm com prior_covariance = decov(1)³.

Para eficiência computacional o rstanarm modifica a matriz de covariância $\boldsymbol{\Sigma}$. Especificamente, fazemos com que ela vire uma matriz de correlação. Toda matriz de covariância pode ser decomposta em:

\[ \boldsymbol{\Sigma}=\text{diag}_\text{matrix}(\boldsymbol{\tau}) \cdot \boldsymbol{\Omega} \cdot \text{diag}_\text{matrix}(\boldsymbol{\tau}) \]

na qual $\boldsymbol{\Omega}$ é uma matriz de correlação com $1$ na sua diagonal e os demais elementos entre -1 e 1 $\rho \in (-1, 1)$. $\boldsymbol{\tau}$ é um vetor composto pelas variâncias das variáveis de $\boldsymbol{\Sigma}$ (a diagonal de $\boldsymbol{\Sigma}$).

Adicionalmente a matriz de correlação $\boldsymbol{\Omega}$ pode ser decomposta mais uma vez para maior eficiência computacional. Como toda matriz de correlação é simétrica e definitiva positiva (todos seus autovalores são numeros reais $\mathbb{R}$ e positivos $>0$), podemos usar a Decomposição Cholesky para decompô-la em uma matriz triangular (que é muito mais eficiente computacionalmente):

\[ \boldsymbol{\Omega} = \mathbf{L}_\Omega \mathbf{L}^T_\Omega \]

onde $\mathbf{L}_\Omega$ é uma matriz triangular.

O que falta é definirmos então uma priori para a matriz de correlação $\boldsymbol{\Omega}$. Até pouco tempo atrás, usávamos uma distribuição de Wishart como priori (Gelman et al., 2013). Mas essa prática foi abandonada após a proposição da distribuição LKJ de Lewandowski, Kurowicka, & Joe (2009) (LKJ são os nomes dos autores – Lewandowski, Kurowicka e Joe) como priori de matrizes de correlação.

Enfim, embaixo do capô rstanarm faz todas essas decomposições e transformações para nós, sem termos que nos preocupar.

Exemplo com o dataset `cheese`

O dataset cheese (Boatwright, McCulloch, & Rossi, 1999) possui 160 observações de avaliações de queijo. Um grupo de 10 avaliadores “rurais” e 10 “urbanos” avaliaram 4 queijos diferentes $(A,B,C,D)$ em duas amostras. Portanto $4 \cdot 20 \cdot 2 = 160$. Possui 4 variáveis:

cheese: tipo do queijo, $(A,B,C,D)$
rater: avaliador, $(1,\dots, 10)$
background: origem do avaliador em “urbano” ou “rural”
y: variável dependente, nota da avaliação

cheese <- read_csv2("datasets/cheese.csv", col_types = "fffi")

Como sempre eu gosto de usar o pacote skimr (Waring et al., 2021) com a função skim():

library(skimr)
skim(cheese)

Table 1: Data summary
Name	cheese
Number of rows	160
Number of columns	4
_______________________
Column type frequency:
factor	3
numeric	1
________________________
Group variables	None

Variable type: factor

skim_variable	complete_rate	ordered	n_unique	top_counts
cheese	1	FALSE	4	A: 40, B: 40, C: 40, D: 40
rater	1	FALSE	10	1: 16, 2: 16, 3: 16, 4: 16
background	1	FALSE	2	rur: 80, urb: 80

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
y	0	1	71	12	33	64	72	80	91	▁▂▆▇▆

Random-Intercept Model

No primeiro exemplo vamos usar um modelo que cada grupo de cheese recebe uma constante diferente:

# Detectar quantos cores/processadores
options(mc.cores = parallel::detectCores())
options(Ncpus = parallel::detectCores())

library(rstanarm)
random_intercept <- stan_glmer(
  y ~ (1 | cheese) + background,
  data = cheese,
  prior_intercept = normal(mean(cheese$y), 2.5 * sd(cheese$y)),
  prior_covariance = decov(1)
)

No sumário do modelo random-intercept vemos que os avaliadores urbanos avaliam melhor os queijos que os avaliadores rurais, mas também observamos que cada queijo possui uma “taxa basal” de avaliação (cada queijo tem sua constante). Sendo $B$ o pior queijo e $C$ o melhor queijo:

summary(random_intercept)


Model Info:
 function:     stan_glmer
 family:       gaussian [identity]
 formula:      y ~ (1 | cheese) + background
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 160
 groups:       cheese (4)

Estimates:
                                        mean   sd    10%   50%   90%
(Intercept)                            67.3    5.5  60.8  67.2  73.8
backgroundurban                         7.4    1.1   5.9   7.4   8.9
b[(Intercept) cheese:A]                 3.7    5.6  -2.8   3.9  10.4
b[(Intercept) cheese:B]               -14.2    5.6 -20.9 -14.0  -7.6
b[(Intercept) cheese:C]                 8.4    5.6   1.9   8.5  15.2
b[(Intercept) cheese:D]                 1.3    5.6  -5.3   1.4   8.0
sigma                                   7.1    0.4   6.6   7.1   7.6
Sigma[cheese:(Intercept),(Intercept)] 131.6  118.4  42.4  95.2 254.7

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 70.9    0.8 69.9  70.9  71.9 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                                      mcse Rhat n_eff
(Intercept)                           0.2  1.0  1315 
backgroundurban                       0.0  1.0  3392 
b[(Intercept) cheese:A]               0.2  1.0  1337 
b[(Intercept) cheese:B]               0.2  1.0  1346 
b[(Intercept) cheese:C]               0.2  1.0  1349 
b[(Intercept) cheese:D]               0.2  1.0  1343 
sigma                                 0.0  1.0  3576 
Sigma[cheese:(Intercept),(Intercept)] 3.0  1.0  1579 
mean_PPD                              0.0  1.0  3719 
log-posterior                         0.1  1.0  1241 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Vamos verificar o Posterior Predictive Check do modelo random-intercept na figura 3:

pp_check(random_intercept)

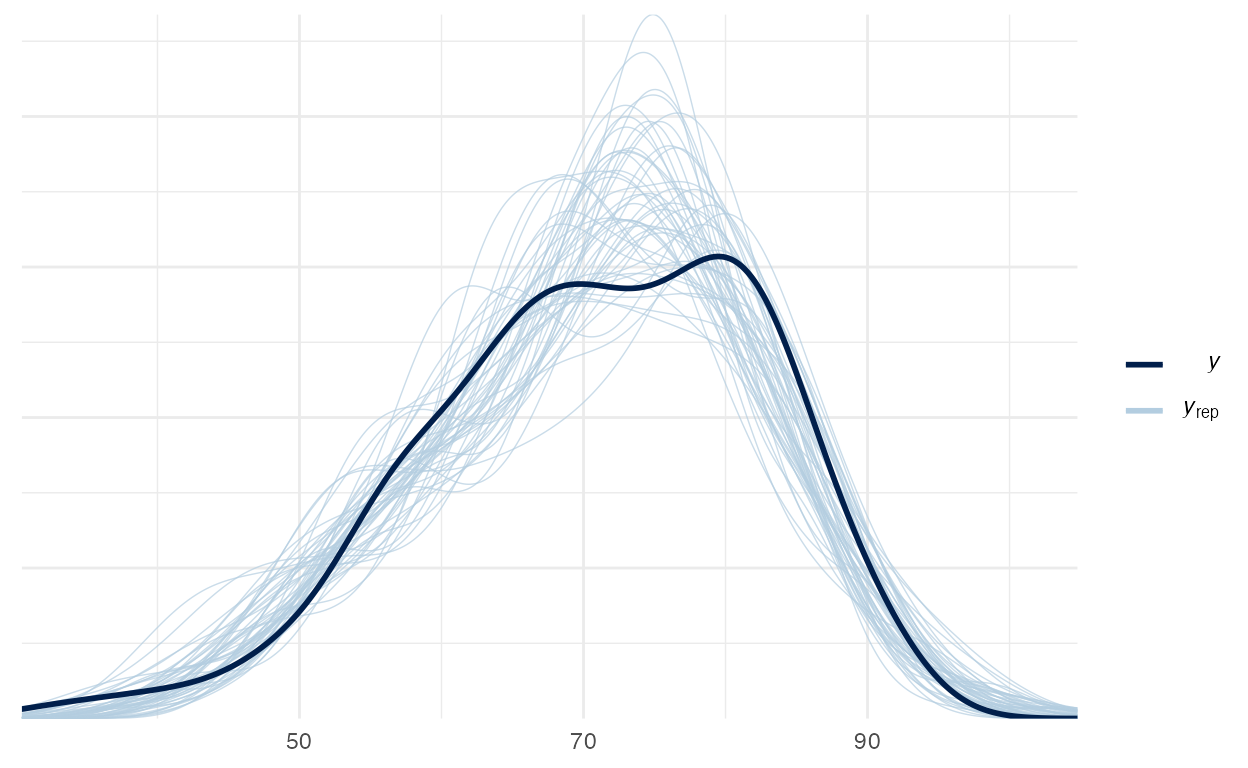
Figure 3: Posterior Preditive Check do modelo random-intercept

Random-Slope Model

No segundo exemplo vamos usar um modelo que cada grupo de cheese recebe um coeficiente diferente para background:

random_slope <- stan_glmer(
  y ~ (0 + background | cheese),
  data = cheese,
  prior_intercept = normal(mean(cheese$y), 2.5 * sd(cheese$y)),
  prior_covariance = decov(1)
)

Aqui vemos que todos os queijos recebem a mesma constante mas cada queijo possui um coeficiente diferente para background do avaliador:

summary(random_slope)


Model Info:
 function:     stan_glmer
 family:       gaussian [identity]
 formula:      y ~ (0 + background | cheese)
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 160
 groups:       cheese (4)

Estimates:
                                                mean   sd    10%
(Intercept)                                    69.9    5.9  62.9
b[backgroundrural cheese:A]                     0.8    6.0  -6.5
b[backgroundurban cheese:A]                     8.8    6.1   1.5
b[backgroundrural cheese:B]                   -15.7    6.2 -23.2
b[backgroundurban cheese:B]                   -10.3    5.9 -17.4
b[backgroundrural cheese:C]                     5.4    5.9  -1.9
b[backgroundurban cheese:C]                    13.7    6.1   6.2
b[backgroundrural cheese:D]                    -0.7    6.0  -7.7
b[backgroundurban cheese:D]                     5.4    6.0  -1.9
sigma                                           7.1    0.4   6.6
Sigma[cheese:backgroundrural,backgroundrural] 134.0  121.8  40.6
Sigma[cheese:backgroundurban,backgroundrural]  76.4  102.8   3.4
Sigma[cheese:backgroundurban,backgroundurban] 167.7  164.0  52.2
                                                50%   90%
(Intercept)                                    70.1  76.9
b[backgroundrural cheese:A]                     0.7   7.9
b[backgroundurban cheese:A]                     8.5  16.0
b[backgroundrural cheese:B]                   -15.8  -8.1
b[backgroundurban cheese:B]                   -10.4  -3.3
b[backgroundrural cheese:C]                     5.2  12.5
b[backgroundurban cheese:C]                    13.5  21.1
b[backgroundrural cheese:D]                    -0.7   6.5
b[backgroundurban cheese:D]                     5.3  12.9
sigma                                           7.1   7.6
Sigma[cheese:backgroundrural,backgroundrural]  99.0 262.6
Sigma[cheese:backgroundurban,backgroundrural]  52.6 172.9
Sigma[cheese:backgroundurban,backgroundurban] 120.3 328.3

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 70.8    0.8 69.8  70.8  71.8 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                                              mcse Rhat n_eff
(Intercept)                                   0.2  1.0   722 
b[backgroundrural cheese:A]                   0.2  1.0   726 
b[backgroundurban cheese:A]                   0.2  1.0   744 
b[backgroundrural cheese:B]                   0.2  1.0   738 
b[backgroundurban cheese:B]                   0.2  1.0   774 
b[backgroundrural cheese:C]                   0.2  1.0   736 
b[backgroundurban cheese:C]                   0.2  1.0   742 
b[backgroundrural cheese:D]                   0.2  1.0   744 
b[backgroundurban cheese:D]                   0.2  1.0   721 
sigma                                         0.0  1.0  3567 
Sigma[cheese:backgroundrural,backgroundrural] 2.8  1.0  1958 
Sigma[cheese:backgroundurban,backgroundrural] 3.0  1.0  1140 
Sigma[cheese:backgroundurban,backgroundurban] 5.0  1.0  1077 
mean_PPD                                      0.0  1.0  3749 
log-posterior                                 0.1  1.0  1105 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Vamos verificar o Posterior Predictive Check do modelo random-slope na figura 4:

pp_check(random_slope)

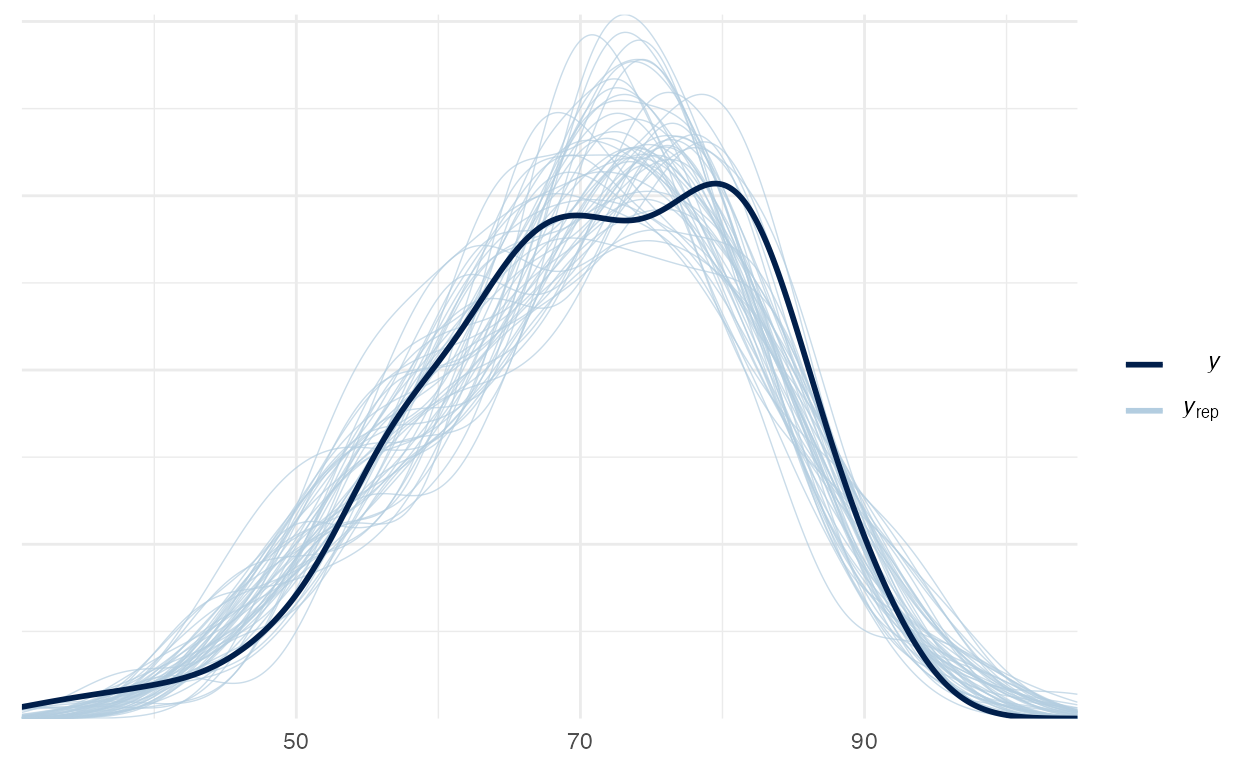
Figure 4: Posterior Preditive Check do modelo random-slope

Random-Intercept-Slope Model

No terceiro exemplo vamos usar um modelo que cada grupo de cheese recebe uma constante diferente e um coeficiente diferente para background:

random_intercept_slope <- stan_glmer(
  y ~ (1 + background | cheese),
  data = cheese,
  prior_intercept = normal(mean(cheese$y), 2.5 * sd(cheese$y)),
  prior_covariance = decov(1)
)

Aqui vemos que os queijos recebem a constantes diferentes e que cada queijo possui um coeficiente diferente para background do avaliador:

summary(random_intercept_slope)


Model Info:
 function:     stan_glmer
 family:       gaussian [identity]
 formula:      y ~ (1 + background | cheese)
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 160
 groups:       cheese (4)

Estimates:
                                                mean   sd    10%
(Intercept)                                    65.0    7.6  55.4
b[(Intercept) cheese:A]                         5.8    7.6  -3.3
b[backgroundurban cheese:A]                     7.8    2.2   5.0
b[(Intercept) cheese:B]                       -10.5    7.9 -20.0
b[backgroundurban cheese:B]                     4.6    2.3   1.6
b[(Intercept) cheese:C]                        10.2    7.5   1.1
b[backgroundurban cheese:C]                     8.4    2.2   5.5
b[(Intercept) cheese:D]                         4.2    7.6  -4.8
b[backgroundurban cheese:D]                     6.0    2.2   3.3
sigma                                           7.1    0.4   6.6
Sigma[cheese:(Intercept),(Intercept)]         157.1  168.0  43.7
Sigma[cheese:backgroundurban,(Intercept)]      24.5   76.0 -46.8
Sigma[cheese:backgroundurban,backgroundurban]  84.9   81.0  25.2
                                                50%   90%
(Intercept)                                    65.2  74.0
b[(Intercept) cheese:A]                         5.6  15.4
b[backgroundurban cheese:A]                     7.8  10.6
b[(Intercept) cheese:B]                       -10.5  -0.8
b[backgroundurban cheese:B]                     4.6   7.6
b[(Intercept) cheese:C]                        10.1  19.7
b[backgroundurban cheese:C]                     8.4  11.2
b[(Intercept) cheese:D]                         4.1  13.8
b[backgroundurban cheese:D]                     6.1   8.8
sigma                                           7.1   7.7
Sigma[cheese:(Intercept),(Intercept)]         111.1 308.9
Sigma[cheese:backgroundurban,(Intercept)]      17.0 102.5
Sigma[cheese:backgroundurban,backgroundurban]  60.7 165.7

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 70.8    0.8 69.8  70.8  71.9 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                                              mcse Rhat n_eff
(Intercept)                                   0.3  1.0   788 
b[(Intercept) cheese:A]                       0.3  1.0   810 
b[backgroundurban cheese:A]                   0.0  1.0  4942 
b[(Intercept) cheese:B]                       0.3  1.0   786 
b[backgroundurban cheese:B]                   0.0  1.0  2615 
b[(Intercept) cheese:C]                       0.3  1.0   804 
b[backgroundurban cheese:C]                   0.0  1.0  4562 
b[(Intercept) cheese:D]                       0.3  1.0   808 
b[backgroundurban cheese:D]                   0.0  1.0  4895 
sigma                                         0.0  1.0  3967 
Sigma[cheese:(Intercept),(Intercept)]         4.2  1.0  1595 
Sigma[cheese:backgroundurban,(Intercept)]     2.4  1.0   989 
Sigma[cheese:backgroundurban,backgroundurban] 1.9  1.0  1746 
mean_PPD                                      0.0  1.0  3604 
log-posterior                                 0.1  1.0  1168 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Por fim, vamos verificar o Posterior Predictive Check do modelo random-intercept-slope na figura 5:

pp_check(random_intercept_slope)

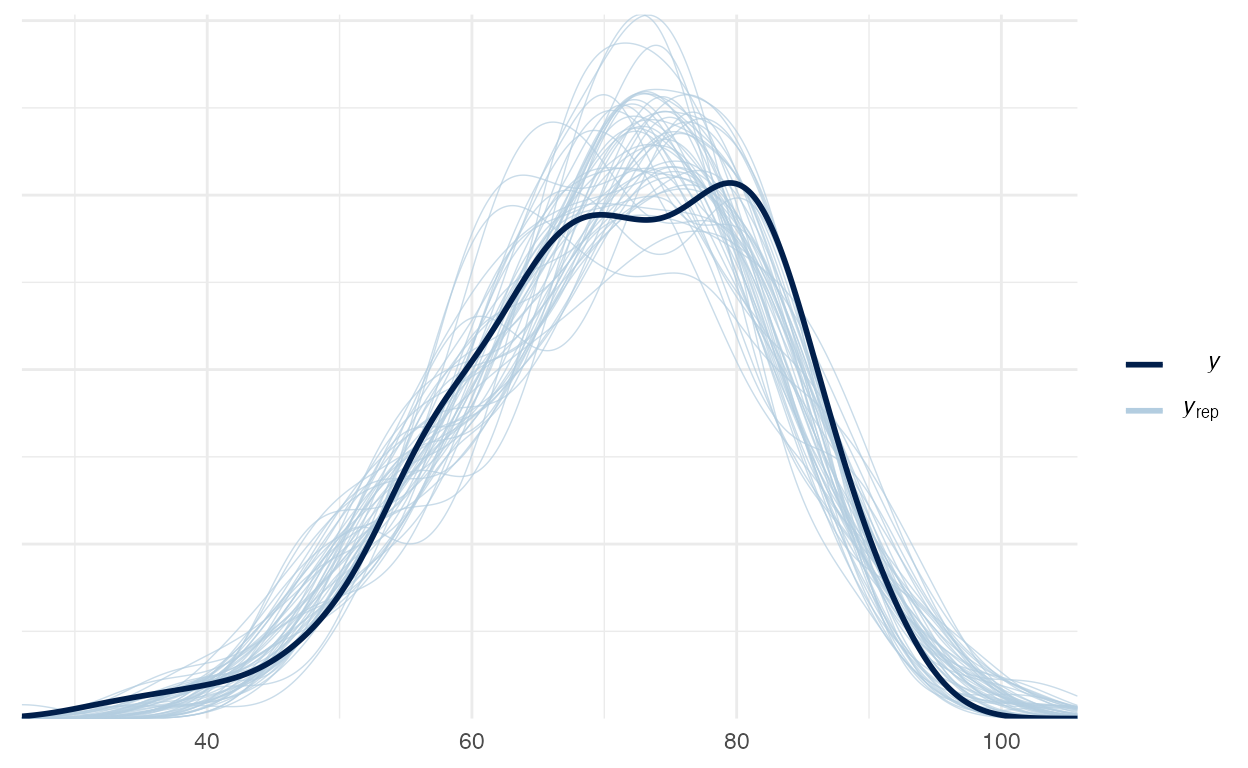
Figure 5: Posterior Preditive Check do modelo random-intercept-slope

Modelos multiníveis no `brms`

O brms tem uma pequena diferença no output do sumário do modelo. Aqui especificamos a priori da matriz de covariância um pouco diferente com prior(lkj_corr_cholesky(1), class = L) que é o mesmo que prior_covariance = decov(1) do rstanarm:

OBS: 79 é a média de cheese$y e 21 é 2.5x o desvio padrão de cheese$y.

library(brms)

brms_random_intercept_slope <- brm(
  y ~ (1 + background | cheese),
  data = cheese,
  prior = c(
    prior(normal(71, 29), class = Intercept),
    prior(lkj_corr_cholesky(1), class = L)
  )
)

Veja o output do summary() para modelos multiníveis estimados pelo brms:

summary(brms_random_intercept_slope)

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: y ~ (1 + background | cheese) 
   Data: cheese (Number of observations: 160) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Group-Level Effects: 
~cheese (Number of levels: 4) 
                               Estimate Est.Error l-95% CI u-95% CI
sd(Intercept)                     13.23      6.06     5.60    28.38
sd(backgroundurban)                9.03      3.99     3.98    18.50
cor(Intercept,backgroundurban)     0.22      0.52    -0.78     0.97
                               Rhat Bulk_ESS Tail_ESS
sd(Intercept)                  1.00     1406     1827
sd(backgroundurban)            1.00     1420     1980
cor(Intercept,backgroundurban) 1.00      700     1411

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept    64.89      8.71    47.06    82.75 1.00      699      967

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     7.11      0.42     6.34     7.99 1.00     2700     2398

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Não há menção dos efeitos de grupo. Para isso precisamos usar a função ranef() (uma abreviação de random effects). Caso queira somente os efeitos populacionais pode usar a função fixef() (uma abreviação de fixed effects):

ranef(brms_random_intercept_slope)

$cheese
, , Intercept

  Estimate Est.Error  Q2.5 Q97.5
A      5.9       8.7 -11.8  23.9
B    -10.4       9.0 -28.8   7.7
C     10.4       8.7  -7.5  28.4
D      4.4       8.7 -13.9  22.6

, , backgroundurban

  Estimate Est.Error Q2.5 Q97.5
A      7.8       2.1 3.57  12.1
B      4.7       2.3 0.33   9.4
C      8.4       2.1 4.18  12.6
D      6.0       2.1 1.99  10.3

Atividade Prática

Para atividade prática, temos o dataset rikz(Zuur, Ieno, & Smith, 2007) no diretório datasets/ (figura 6). Segue a descrição em inglês do dataset.

For each of 9 intertidal areas (denoted ‘Beaches’), the researchers sampled five sites (denoted ‘Sites’) and at each site they measured abiotic variables and the diversity of macro-fauna (e.g. aquatic invertebrates). Here, species richness refers to the total number of species found at a given site while NAP ( i.e. Normal Amsterdams Peil) refers to the height of the sampling location relative to the mean sea level and represents a measure of the amount of food available for birds, etc. For our purpose, the main question is:

What is the influence of NAP on species richness?

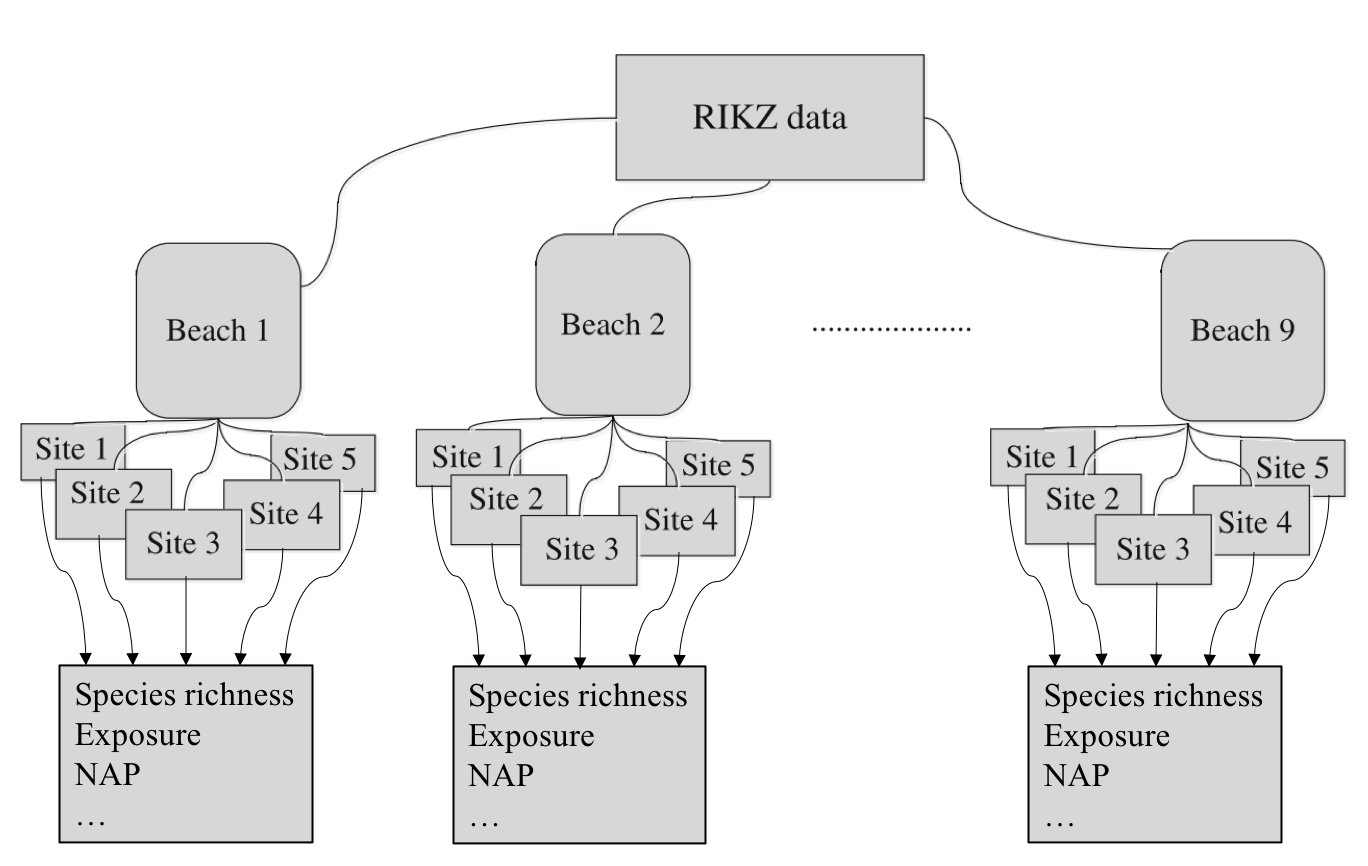
Figure 6: Dataset rikz

rikz <- read_csv2("datasets/rikz.csv", col_types = "iidff")

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] brms_2.15.0     rstanarm_2.21.1 Rcpp_1.0.6      skimr_2.1.3    
 [5] readr_1.4.0     readxl_1.3.1    tibble_3.1.2    ggplot2_3.3.3  
 [9] patchwork_1.1.1 cowplot_1.1.1  

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         repr_1.1.3           splines_4.1.0       
  [7] crosstalk_1.1.1      rstantools_2.1.1     inline_0.3.19       
 [10] digest_0.6.27        htmltools_0.5.1.1    magick_2.7.2        
 [13] rsconnect_0.8.18     fansi_0.5.0          magrittr_2.0.1      
 [16] RcppParallel_5.1.4   matrixStats_0.59.0   xts_0.12.1          
 [19] prettyunits_1.1.1    colorspace_2.0-1     textshaping_0.3.4   
 [22] xfun_0.23            dplyr_1.0.6          callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] gtable_0.3.0         V8_3.4.2             pkgbuild_1.2.0      
 [34] rstan_2.21.2         abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] xtable_1.8-4         stats4_4.1.0         StanHeaders_2.21.0-7
 [43] DT_0.18              htmlwidgets_1.5.3    threejs_0.3.3       
 [46] ellipsis_0.3.2       pkgconfig_2.0.3      loo_2.4.1           
 [49] farver_2.1.0         sass_0.4.0           utf8_1.2.1          
 [52] tidyselect_1.1.1     labeling_0.4.2       rlang_0.4.11        
 [55] reshape2_1.4.4       later_1.2.0          munsell_0.5.0       
 [58] cellranger_1.1.0     tools_4.1.0          cli_2.5.0           
 [61] generics_0.1.0       ggridges_0.5.3       evaluate_0.14       
 [64] stringr_1.4.0        fastmap_1.1.0        yaml_2.2.1          
 [67] ragg_1.1.2           processx_3.5.2       knitr_1.33          
 [70] purrr_0.3.4          nlme_3.1-152         mime_0.10           
 [73] projpred_2.0.2       xml2_1.3.2           compiler_4.1.0      
 [76] bayesplot_1.8.0      shinythemes_1.2.0    rstudioapi_0.13     
 [79] curl_4.3.1           gamm4_0.2-6          png_0.1-7           
 [82] bslib_0.2.5.1        stringi_1.6.2        highr_0.9           
 [85] ps_1.6.0             Brobdingnag_1.2-6    lattice_0.20-44     
 [88] Matrix_1.3-3         nloptr_1.2.2.2       markdown_1.1        
 [91] shinyjs_2.0.0        vctrs_0.3.8          pillar_1.6.1        
 [94] lifecycle_1.0.0      jquerylib_0.1.4      bridgesampling_1.1-2
 [97] httpuv_1.6.1         R6_2.5.0             bookdown_0.22       
[100] promises_1.2.0.1     gridExtra_2.3        codetools_0.2-18    
[103] distill_1.2          boot_1.3-28          colourpicker_1.1.0  
[106] MASS_7.3-54          gtools_3.8.2         assertthat_0.2.1    
[109] rprojroot_2.0.2      withr_2.4.2          shinystan_2.5.0     
[112] mgcv_1.8-35          parallel_4.1.0       hms_1.1.0           
[115] grid_4.1.0           tidyr_1.1.3          coda_0.19-4         
[118] minqa_1.2.4          rmarkdown_2.8        downlit_0.2.1       
[121] shiny_1.6.0          lubridate_1.7.10     base64enc_0.1-3     
[124] dygraphs_1.1.1.6

Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. https://doi.org/10.18637/jss.v067.i01

Boatwright, P., McCulloch, R., & Rossi, P. (1999). Account-level modeling for trade promotion: An application of a constrained parameter hierarchical model. Journal of the American Statistical Association, 94(448), 1063–1073.

de Finetti, B. (1974). Theory of Probability (Volume 1). New York: John Wiley & Sons.

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis. Chapman and Hall/CRC.

Lewandowski, D., Kurowicka, D., & Joe, H. (2009). Generating random correlation matrices based on vines and extended onion method. Journal of Multivariate Analysis, 100(9), 1989–2001.

Nau, R. F. (2001). De Finetti was Right: Probability Does Not Exist. Theory and Decision, 51(2), 89–124. https://doi.org/10.1023/A:1015525808214

Waring, E., Quinn, M., McNamara, A., Arino de la Rubia, E., Zhu, H., & Ellis, S. (2021). Skimr: Compact and flexible summaries of data. Retrieved from https://CRAN.R-project.org/package=skimr

Zuur, A., Ieno, E. N., & Smith, G. M. (2007). Analyzing ecological data. Springer.

do inglês exchangeability.↩︎
por isso que nas fórmulas do R o 1 é interpretado como a constante do modelo. Substitua-o por uma coluna de $0$ de temos um modelo sem constante, por isso o 0 nas fórmulas é interpretado como um modelo ausente de constante.↩︎
decov(1) é basicamente uma priori uniforme.↩︎

Modelos Multiníveis Bayesianos

Quando usar Modelos Multiníveis?

Hiperpriori (Hyperprior)

Abordagem Frequentista vs Abordagem Bayesiana

Três abordagens de Modelos Multiníveis

Random-Intercept Model

Random-Slope Model

Random-Intercept-Slope Model

Prioris de Modelos Multiníveis

Exemplo com o dataset `cheese`

Random-Intercept Model

Random-Slope Model

Random-Intercept-Slope Model

Modelos multiníveis no `brms`

Atividade Prática

Ambiente

References

Corrections

Reuse

Citation

Modelos Multiníveis Bayesianos

Quando usar Modelos Multiníveis?

Hiperpriori (Hyperprior)

Abordagem Frequentista vs Abordagem Bayesiana

Três abordagens de Modelos Multiníveis

Random-Intercept Model

Random-Slope Model

Random-Intercept-Slope Model

Prioris de Modelos Multiníveis

Exemplo com o dataset cheese

Random-Intercept Model

Random-Slope Model

Random-Intercept-Slope Model

Modelos multiníveis no brms

Atividade Prática

Ambiente

References

Corrections

Reuse

Citation

Exemplo com o dataset `cheese`

Modelos multiníveis no `brms`