Regressão Linear Bayesiana

Modelos Lineares Generalizados – Gaussiano/Normal

“All models are wrong but some are useful”

Box (1976)

Esta aula começa com uma citação bem provocante do estatístico George Box (figura 1) sobre modelos estatísticos. Sim, todos os modelos de alguma maneira estão errados. Mas eles são muito úteis. A ideia é que a realidade é muito complexa para nós compreendermos ao analisarmos de maneira nua e crua. Precisamos de alguma maneira simplificá-la em componentes individuais e analisar as suas relações. Mas aqui há um perigo: qualquer simplificação da realidade promove perda de informação de alguma maneira. Portanto sempre temos um equilíbrio delicado entre simplificações da realidade por meio de modelos e a inerente perda de informação. Agora você me pergunta: como eles são úteis? Imagine que você está no escuro total e você possui uma lanterna muito potente mas com um foco de iluminação estreito. Você não vai jogar a lanterna fora porque ela não consegue iluminar tudo ao seu redor e ficar no escuro? Você deve usar a lanterna para apontar para locais interessantes da escuridão e iluminá-los. Você nunca achará uma lanterna que ilumine tudo com a clareza que você precisa para analisar todos os detalhes da realidade. Assim como você nunca achará um modelo único que explicará toda a realidade ao seu redor. Você precisa de diferentes lanternas assim como precisa de diferentes modelos. Sem eles você ficará no escuro.

Figure 1: George Box. Figura de https://www.wikipedia.org

Regressão Linear

Vamos falar de um classe de modelo conhecido como regressão linear. A ideia aqui é modelar uma variável dependente sendo a combinação linear de variáveis independentes.

\[ \boldsymbol{y} = \alpha + \mathbf{X} \boldsymbol{\beta} + \epsilon \]

Sendo que:

• \(\boldsymbol{y}\) – variável dependente
• \(\alpha\) – constante (também chamada de intercept)
• \(\boldsymbol{\beta}\) – vetor de coeficientes
• \(\mathbf{X}\) – matriz de dados
• \(\epsilon\) – erro do modelo

Para estimar a constante \(\alpha\) e os coeficientes \(\boldsymbol{\beta}\) usamos uma função de verosimilhança Gaussiana/normal. Matematicamente o modelo de regressão Bayesiano é

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Normal}\left( \alpha + \mathbf{X} \boldsymbol{\beta}, \sigma \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \\ \sigma &\sim \text{Exponencial}(\lambda_\sigma) \end{aligned} \]

Aqui vemos que a função de verosimilhança \(P(\boldsymbol{y} \mid \boldsymbol{\theta})\) é uma distribuição normal na qual \(\boldsymbol{y}\) depende dos parâmetros do modelo \(\alpha\) e \(\boldsymbol{\beta}\), além de termos um erro \(\sigma\). Condicionamos \(\boldsymbol{y}\) nos dados observados \(\mathbf{X}\) ao inserimos \(\alpha + \mathbf{X} \boldsymbol{\beta}\) como o preditor linear do modelo (a média \(\mu\) da função de verosimilhança do modelo). O que falta é especificar quais são as prioris dos parâmetros do modelo:

• Distribuição priori de \(\alpha\) – Conhecimento que temos da constante do modelo
• Distribuição priori de \(\boldsymbol{\beta}\) – Conhecimento que temos dos coeficientes das variáveis independentes do modelo
• Distribuição priori de \(\sigma\) – Conhecimento que temos sobre o erro do modelo. Importante que o erro pode ser somente positivo. Além disso é intuitivo colocar uma distribuição que dê peso maior para valores próximos de zero, mas que permita também valores distantes de zero, portanto uma distribuição com cauda longa é bem-vinda. Distribuições candidatas são a \(\text{Exponencial}\) que só tem suporte nos numeros reais positivos (então já resolve a questão de erros negativos) ou a \(\text{Cauchy}^+\) truncada para apenas números positivos (lembrando que a distribuição Cauchy é a \(t\) de Student com graus de liberdade \(\nu = 1\))

Stan instanciará um modelo bayesiano com os dados fornecidos (\(\boldsymbol{y}\) e \(\mathbf{X}\)) e encontrará a distribuição posterior dos parâmetros de interesse do modelo (\(\alpha\) e \(\boldsymbol{\beta}\)) calculando a distribuição posterior completa de:

\[ P(\boldsymbol{\theta} \mid \boldsymbol{y}) = P(\alpha, \boldsymbol{\beta}, \sigma \mid \boldsymbol{y}) \]

Posterior Predictive Check

Lembrando o fluxo de trabalho que discutimos na Aula - Priors (Figura 2)

Figure 2: Bayesian Workflow. Baseado em Gelman et al. (2020)

Precisamos nos certificar que a nossa distribuição posterior de \(\boldsymbol{y}\) consegue capturar todas as nuanças da densidade real de \(\boldsymbol{y}\). Isto é um procedimento chamado de Posterior Predictive Check e é geralmente auferido com uma inspeção visual da densidade real de \(\boldsymbol{y}\) contrastada com amostragens da densidade posterior de \(\boldsymbol{y}\) estimada pelo modelo Bayesiano. O propósito é comparar o histograma da variável dependente \(\boldsymbol{y}\) contra o histograma variáveis dependentes simuladas pelo modelo \(\boldsymbol{y}_{\text{rep}}\) após a estimação dos parâmetros. A ideia é que os histogramas reais e simulados se misturem e não haja divergências.

Isso pode ser feito tanto no rstanarm quando no brms. Ambos usam o pacote bayesplot (Gabry & Mahr, 2021) para gerar as visualizações¹:

• rstanarm: função pp_check() em qualquer modelo oriundo das funções stan_*()
• brms: função pp_check() em qualquer modelo oriundo da função brm()

Exemplo - Score de QI de crianças

Para o nosso exemplo, usarei um dataset famoso chamado kidiq (Gelman & Hill, 2007) que está incluído no rstanarm. São dados de uma survey de mulheres adultas norte-americanas e seus respectivos filhos. Datado de 2007 possui 434 observações e 4 variáveis:

• kid_score: QI da criança
• mom_hs: binária (0 ou 1) se a mãe possui diploma de ensino médio
• mom_iq: QI da mãe
• mom_age: idade da mãe

Ao todo serão 4 modelos para modelar QI da criança (kid_score). Os primeiros dois modelos terão apenas uma única variável independente (mom_hs ou mom_iq), o terceiro usará duas variáveis independentes (mom_hs + mom_iq) e o quarto incluirá uma interação entre essas duas variáveis independentes (mom_hs * mom_iq).

# Detectar quantos cores/processadores
options(mc.cores = parallel::detectCores())
options(Ncpus = parallel::detectCores())

library(rstanarm)
data(kidiq)

Descritivo das variáveis

Antes de tudo, analise SEMPRE os dados em mãos. Graficamente e com tabelas. Isso pode ajudar a elucidar prioris além de embasar melhor conhecimento de domínio do fenômeno de interesse.

Pessoalmente uso o pacote skimr (Waring et al., 2021) com a função skim():

library(skimr)

skim(kidiq)

Table 1: Data summary

Name	kidiq
Number of rows	434
Number of columns	4
_______________________
Column type frequency:
numeric	4
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
kid_score	0	1	86.80	20.41	20	74	90	102	144	▁▃▇▇▁
mom_hs	0	1	0.79	0.41	0	1	1	1	1	▂▁▁▁▇
mom_iq	0	1	100.00	15.00	71	89	98	110	139	▃▇▆▃▂
mom_age	0	1	22.79	2.70	17	21	23	25	29	▂▅▇▃▂

Modelo 1 - mom_hs

Primeiro modelo é apenas a variável mom_hs como variável independente Acredito que se a mãe da criança possui ensino médio isso pode impactar positivamente de 1 a 2 desvio padrões no QI da criança. O que resulta em prior = normal(0, sd(kidiq$kid_score))². Vou colocar a priori da constante \(\alpha\) como uma normal centrada na média do QI da criança e com um desvio padrão 2.5 maior que o desvio padrão do QI da criança. Isto resulta em prior_intercept = normal(mean(kidiq$kid_score), 2.5 * sd(kidiq$kid_score)). Sobre a priori do erro do modelo vou manter o padrão do rstanarm que é uma distribuição exponencial com \(\lambda\) 1 / sd(kidiq$kid_score).

model_1 <- stan_glm(
  kid_score ~ mom_hs,
  data = kidiq,
  prior = normal(0, sd(kidiq$kid_score)),
  prior_intercept = normal(mean(kidiq$kid_score), 2.5 * sd(kidiq$kid_score)),
  prior_aux = rstanarm::exponential(1 / sd(kidiq$kid_score))
  )

Vamos ver como ficaram as estimação dos parâmetros de interesse do modelo com summary():

summary(model_1)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 434
 predictors:   2

Estimates:
              mean   sd   10%   50%   90%
(Intercept) 77.6    2.0 75.0  77.6  80.2 
mom_hs      11.7    2.3  8.7  11.6  14.7 
sigma       19.9    0.7 19.0  19.9  20.8 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 86.8    1.3 85.1  86.8  88.5 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  3873 
mom_hs        0.0  1.0  3804 
sigma         0.0  1.0  3939 
mean_PPD      0.0  1.0  4146 
log-posterior 0.0  1.0  1752 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Não tivemos nenhum problema nas correntes Markov pois todos os Rhat estão bem abaixo de 1.01. Mas o modelo está com um erro alto, \(\sigma \approx 20\). Isto é esperado pois estamos usando apenas uma única variável independente para modelar kid_score.

Vamos verificar o Posterior Predictive Check do modelo 1 na figura 3:

pp_check(model_1)

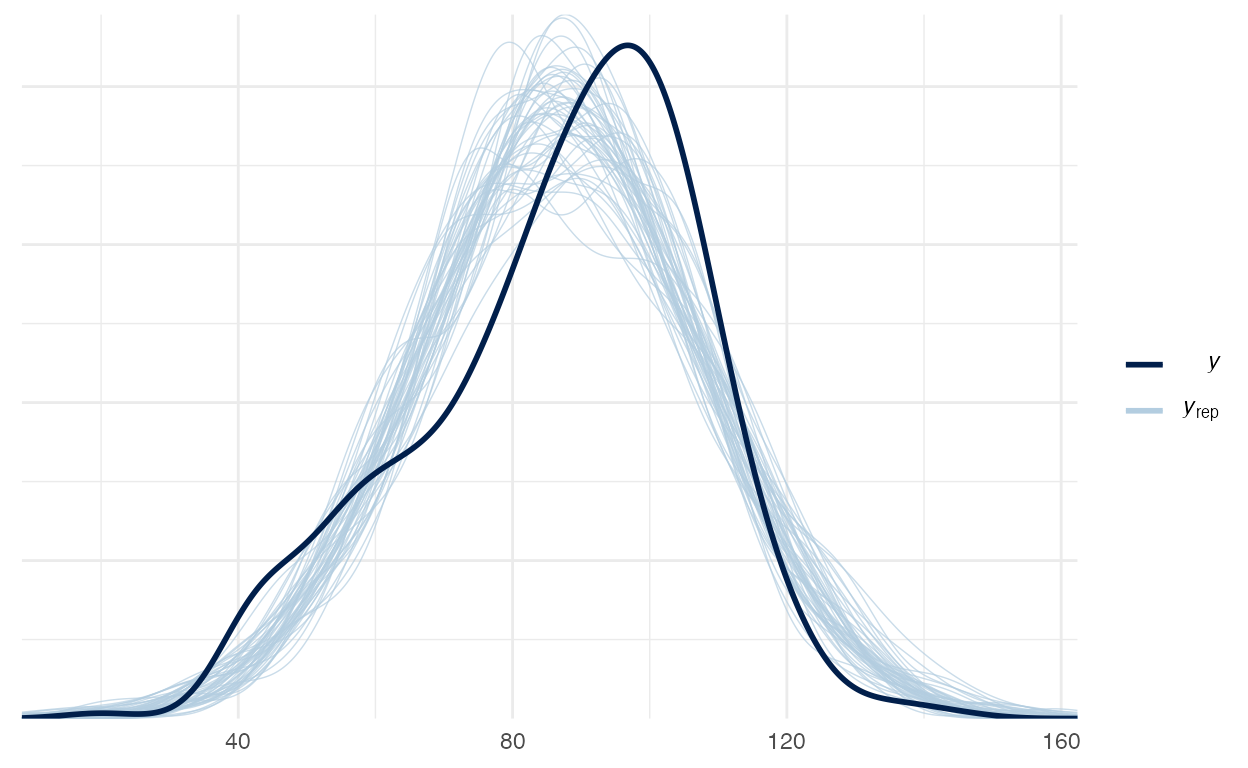
Figure 3: Posterior Preditive Check do modelo 1

Modelo 2 - mom_iq

Segundo modelo é apenas a variável mom_iq como variável independente Vou manter as prioris de \(\alpha\) e \(\lambda\). Para a variável mom_iq acredito que a correlação entre QI da mãe e QI da criança seja positiva e acima de 0.5. Então a minha priori será uma normal centrada em 0.5 com 0.5 de desvio padrão. Isto resulta em prior = normal(0.5, 0.5):

model_2 <- stan_glm(
  kid_score ~ mom_iq,
  data = kidiq,
  prior = normal(0.5, 0.5),
  prior_intercept = normal(mean(kidiq$kid_score), 2.5 * sd(kidiq$kid_score)),
  prior_aux = rstanarm::exponential(1 / sd(kidiq$kid_score))
  )

summary(model_2)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_iq
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 434
 predictors:   2

Estimates:
              mean   sd   10%   50%   90%
(Intercept) 25.9    5.9 18.4  25.8  33.4 
mom_iq       0.6    0.1  0.5   0.6   0.7 
sigma       18.3    0.6 17.6  18.3  19.1 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 86.8    1.2 85.2  86.8  88.4 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.1  1.0  3585 
mom_iq        0.0  1.0  3606 
sigma         0.0  1.0  3297 
mean_PPD      0.0  1.0  4060 
log-posterior 0.0  1.0  1884 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Mais uma vez nenhum problema com as correntes Markov (Rhat menor que 1.01) e o erro do modelo continua em níveis elevados (\(\sigma \approx 18\)). Vamos precisar incorporar mais variáveis no modelo.

Vamos verificar o Posterior Predictive Check do modelo 2 na figura 4:

pp_check(model_2)

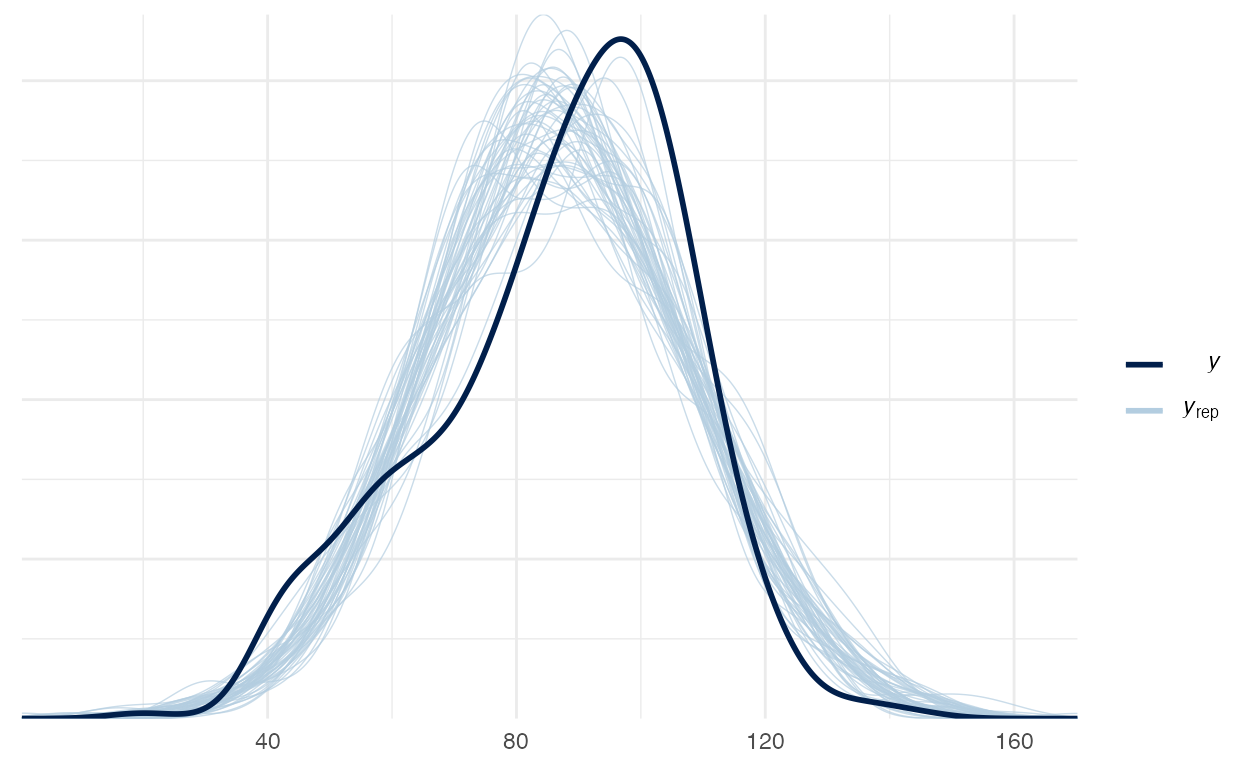
Figure 4: Posterior Preditive Check do modelo 2

Modelo 3 - mom_hs + mom_iq

Terceiro modelo usa as duas variáveis mom_hs e mom_iq como variáveis independentes. Vou manter todas as prioris definidas nos modelos 1 e 2.

model_3 <- stan_glm(
  kid_score ~ mom_hs + mom_iq,
  data = kidiq,
  prior = normal(c(0.0, 0.5), c(sd(kidiq$kid_score), 0.5)),
  prior_intercept = normal(mean(kidiq$kid_score), 2.5 * sd(kidiq$kid_score)),
  prior_aux = rstanarm::exponential(1 / sd(kidiq$kid_score))
  )

summary(model_3)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs + mom_iq
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 434
 predictors:   3

Estimates:
              mean   sd   10%   50%   90%
(Intercept) 25.8    5.8 18.4  25.9  33.1 
mom_hs       5.9    2.2  3.0   5.9   8.7 
mom_iq       0.6    0.1  0.5   0.6   0.6 
sigma       18.2    0.6 17.4  18.2  19.0 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 86.8    1.2 85.2  86.8  88.3 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.1  1.0  4628 
mom_hs        0.0  1.0  4642 
mom_iq        0.0  1.0  4492 
sigma         0.0  1.0  4769 
mean_PPD      0.0  1.0  4176 
log-posterior 0.0  1.0  1728 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Vamos verificar o Posterior Predictive Check do modelo 3 na figura 5:

pp_check(model_3)

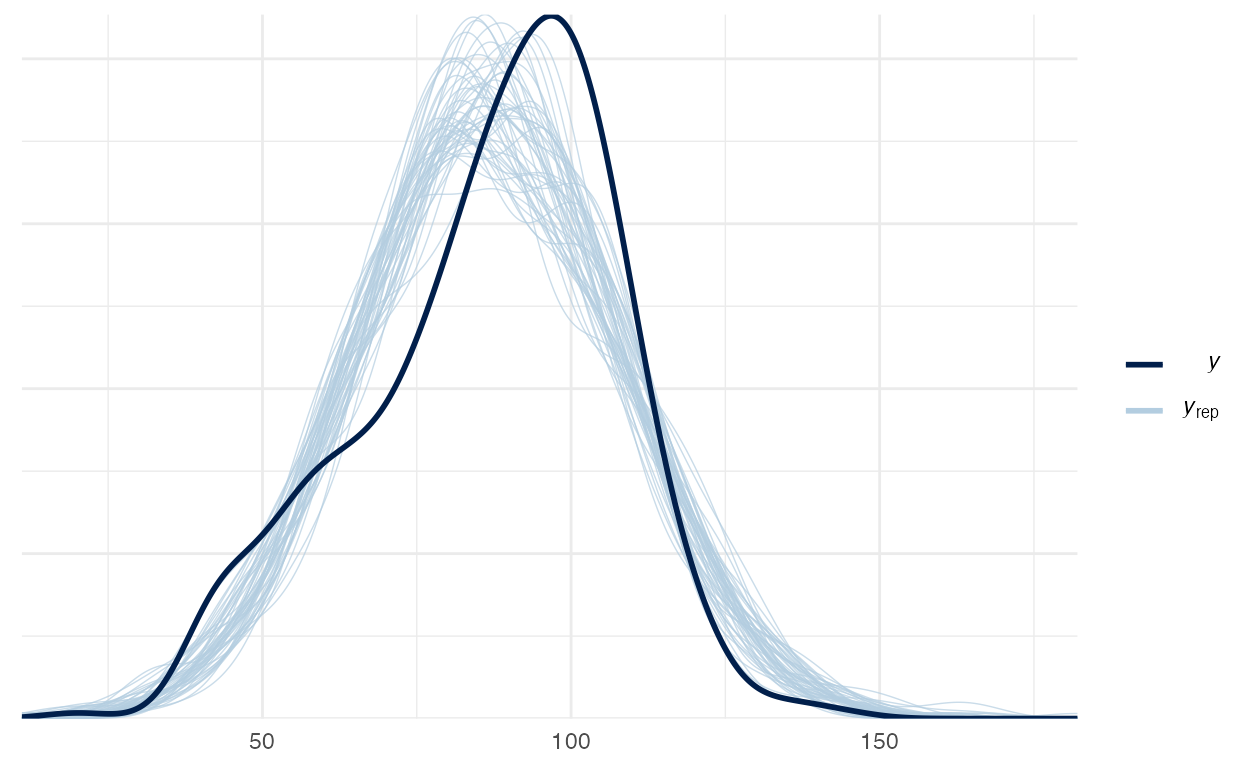
Figure 5: Posterior Preditive Check do modelo 3

Modelo 4 - mom_hs * mom_iq

Quarto modelo usa as duas variáveis mom_hs e mom_iq como variáveis independentes e adiciona uma interação entre as duas. Vou manter as mesmas prioris dos modelos anteriores. Note que a formula agora é atualizada para:

kid_score ~ mom_hs * mom_iq

O operador * na fórmula especifica uma interação entre duas variáveis. O rstanarm (e boa parte as coisas de R que usam a síntaxe de fórmulas y ~ ...) criará uma interação entre as variáveis mom_hs e mom_iq computando matematicamente uma nova variável com o produto das duas e inserindo-a no modelo. Além disso, ao especificarmos uma interação com o * a fórmula se expande para:

mom_hs + mom_iq + mom_hs:mom_iq

Aqui o operador : é também a interação entre as variáveis mom_hs e mom_iq. A diferença entre o operador * e : nas fórmulas é que o operador * aplica o princípio de hierarquia: qualquer efeitos de interação entre variáveis também deve ser inseridos os efeitos principais das variáveis. Se você usar apenas o operador : você está infringindo o princípio de hierarquia. Por isso recomendo em todas suas interações usar sempre o operador * que naturalmente respeita o princípio de hierarquia.

A interação x_1 * x_2 faz o vetor de coeficientes \(\boldsymbol{\beta}\) se tornar:

\[ \boldsymbol{\beta} = \begin{bmatrix} \beta_{x_1} \\ \beta_{x_2} \\ \beta_{x_1} \cdot \beta_{x_2} \end{bmatrix} \]

Note que adicionamos mais uma priori normal ao modelo que é literalmente o produto das duas prioris normais dos coeficientes mom_hs e mom_iq, representando a priori de mom_hs:mom_iq³:

\[ \begin{aligned} \beta_3 &\sim \text{Normal}(\mu_{\beta_1} \cdot \mu_{\beta_2}, \sigma_{\beta_1} \cdot \sigma_{\beta_2}) \\ &\sim \text{Normal}(0 \cdot 0.5, \text{SD}(\boldsymbol{y}) \cdot 0.5) \\ &\sim \text{Normal}\left( 0, \frac{\text{SD}(\boldsymbol{y})}{2} \right) \end{aligned} \]

model_4 <- stan_glm(
  kid_score ~ mom_hs * mom_iq,
  data = kidiq,
  prior = normal(c(0.0, 0.5, 0), c(sd(kidiq$kid_score), 0.5, sd(kidiq$kid_score) * 0.5)),
  prior_intercept = normal(mean(kidiq$kid_score), 2.5 * sd(kidiq$kid_score)),
  prior_aux = rstanarm::exponential(1 / sd(kidiq$kid_score))
  )

summary(model_4)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      kid_score ~ mom_hs * mom_iq
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 434
 predictors:   4

Estimates:
                mean   sd   10%   50%   90%
(Intercept)    5.2   11.1 -9.0   5.3  19.6 
mom_hs        31.1   11.8 15.9  31.3  46.1 
mom_iq         0.8    0.1  0.6   0.8   0.9 
mom_hs:mom_iq -0.3    0.1 -0.4  -0.3  -0.1 
sigma         18.0    0.6 17.3  18.0  18.8 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 86.8    1.2 85.2  86.8  88.4 

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.3  1.0  1197 
mom_hs        0.3  1.0  1169 
mom_iq        0.0  1.0  1169 
mom_hs:mom_iq 0.0  1.0  1092 
sigma         0.0  1.0  2376 
mean_PPD      0.0  1.0  2740 
log-posterior 0.0  1.0  1396 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

O erro do modelo ainda continua elevado, \(\sigma \approx 18\), mas acredito que com estas 2 variáveis é o melhor que podemos fazer com uma função de verosimilhança Gaussiana/Normal.

Vamos verificar o Posterior Predictive Check do modelo 4 na figura 6:

pp_check(model_4)

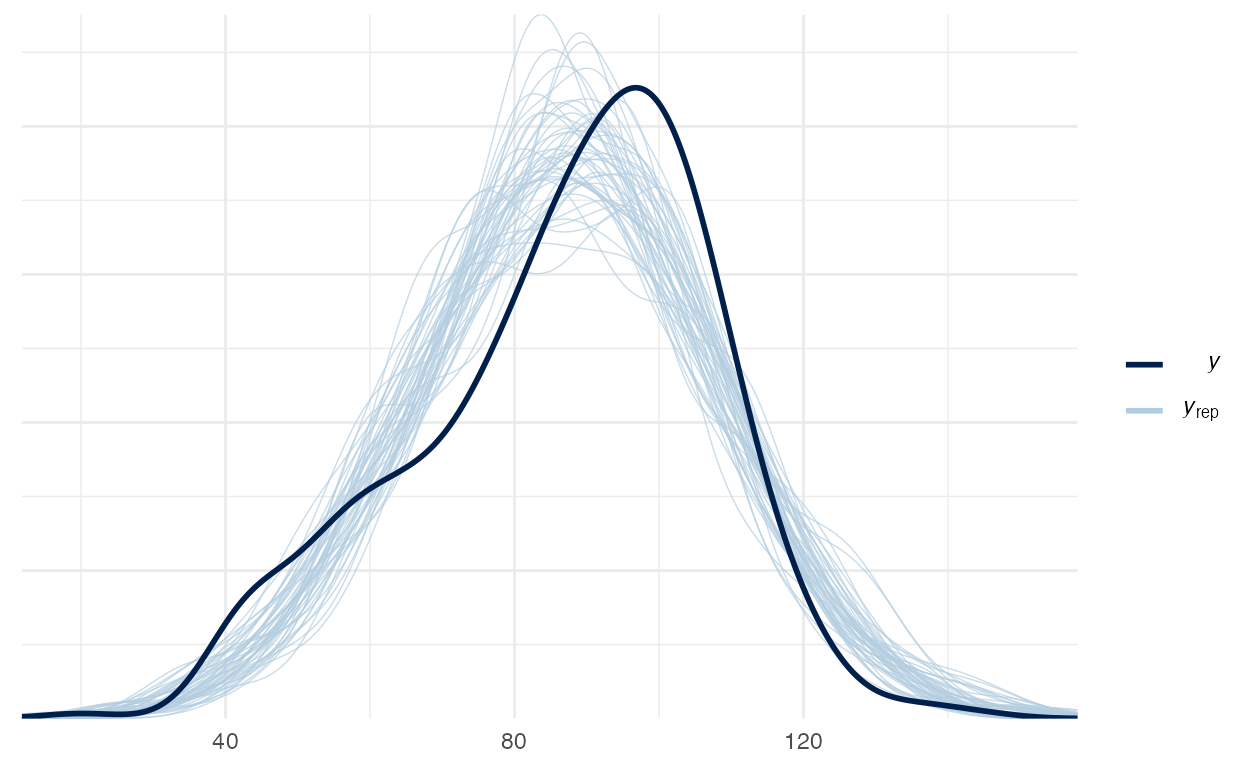
Figure 6: Posterior Preditive Check do modelo 4

Dentre os 4 modelos que usamos os Posterior Predictive Check estão muito próximos. Acredito que há uma leve vantagem dos modelos 3 e 4 sobre os modelo 1 e 2 ao inspecionarmos visualmente os Posterior Predictive Check. Para aprofundar-se em comparação de modelos veja a Aula - Comparação de Modelos, na qual saímos de inspeções visuais (arbitrárias) para métricas de comparação (objetivas).

Variáveis qualitativas

Para as variáveis qualitativas, o R usa um tipo especial de variável chamado factor. A codificação é em números inteiros \(1,2,\dots,K\) mas a relação é distinta/nominal. Ou seja 1 é distinto de 2 e não 1 é 2x menor que 2. Não há relação quantitativa entre os valores das variáveis factor.

Isso resolve o problema de termos variáveis qualitativas (também chamadas de dummy) em modelos de regressão. Para um factor com \(K\) quantidade de classes distintas, temos a possibilidade de criar \(K-1\) coeficientes de regressão. Um para cada classe e usando uma como basal (baseline).

Veja o exemplo usando o pacote gapminder (Bryan, 2017) que convenientemente traz os dados do site gapminder.org para usarmos no R. Temos 5 continentes codificados como uma variável factor chamada continent.

library(gapminder)
levels(gapminder$continent)

[1] "Africa"   "Americas" "Asia"     "Europe"   "Oceania" 

model_5 <- stan_glm(lifeExp ~ gdpPercap + factor(continent), data = gapminder)

print(model_5)

stan_glm
 family:       gaussian [identity]
 formula:      lifeExp ~ gdpPercap + factor(continent)
 observations: 1704
 predictors:   6
------
                          Median MAD_SD
(Intercept)               47.9    0.4  
gdpPercap                  0.0    0.0  
factor(continent)Americas 13.6    0.6  
factor(continent)Asia      8.6    0.6  
factor(continent)Europe   17.6    0.6  
factor(continent)Oceania  18.1    1.8  

Auxiliary parameter(s):
      Median MAD_SD
sigma 8.4    0.1   

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg

Veja que temos 4 variáveis independentes no modelo rstanarm com dados do gapminder (exatamente \(K-1\) como mencionado acima). O R por padrão usa a ordenação alfabética na hora de ordenar os níveis das variáveis qualitativa. Portando o valor Africa da variável continent foi selecionado como nível basal de referência pois é o que aparecerá primeiro numa ordenação alfabética dos 5 valores de continent.

OBS: para mudar o nível basal de referência de uma variável factor use a função relevel() do R ou fct_relevel() do pacote forcats do tidyverse.

Atividade Prática

Dois datasets estão disponíveis no diretório datasets/:

1. WHO Life Expectancy Kaggle Dataset: datasets/WHO_Life_Exp.csv
2. Wine Quality Kaggle Dataset: datasets/Wine_Quality.csv

WHO Life Expectancy

Esse dataset possui 193 países nos últimos 15 anos.

Variáveis

• country
• year
• status
• life_expectancy
• adult_mortality
• infant_deaths
• alcohol
• percentage_expenditure
• hepatitis_b
• measles
• bmi
• under_five_deaths
• polio
• total_expenditure
• diphtheria
• hiv_aids
• gdp
• population
• thinness_1_19_years
• thinness_5_9_years
• income_composition_of_resources
• schooling

Wine Quality Kaggle Dataset

Esse dataset possui 1599 vinhos e estão relacionados com variantes tintas do vinho “Vinho Verde” português. Para mais detalhes, consulte Cortez, Cerdeira, Almeida, Matos, & Reis (2009). Devido a questões de privacidade e logística, apenas variáveis físico-químicas (entradas) e sensoriais (a saída) estão disponíveis (por exemplo, não há dados sobre os tipos de uva, marca de vinho, preço de venda do vinho, etc.).

Variáveis

• fixed_acidity
• volatile_acidity
• citric_acid
• residual_sugar
• chlorides
• free_sulfur_dioxide
• total_sulfur_dioxide
• density
• p_h
• sulphates
• alcohol
• quality

###

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] gapminder_0.3.0      ggExtra_0.9          dplyr_1.0.6         
 [4] rstan_2.21.2         StanHeaders_2.21.0-7 MASS_7.3-54         
 [7] ggforce_0.3.3        gganimate_1.0.7      plotly_4.9.3        
[10] carData_3.0-4        DiagrammeR_1.0.6.1   brms_2.15.0         
[13] rstanarm_2.21.1      Rcpp_1.0.6           skimr_2.1.3         
[16] readr_1.4.0          readxl_1.3.1         tibble_3.1.2        
[19] ggplot2_3.3.3        patchwork_1.1.1      cowplot_1.1.1       

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         lazyeval_0.2.2       repr_1.1.3          
  [7] splines_4.1.0        crosstalk_1.1.1      rstantools_2.1.1    
 [10] inline_0.3.19        digest_0.6.27        htmltools_0.5.1.1   
 [13] magick_2.7.2         rsconnect_0.8.18     fansi_0.5.0         
 [16] magrittr_2.0.1       RcppParallel_5.1.4   matrixStats_0.59.0  
 [19] xts_0.12.1           prettyunits_1.1.1    colorspace_2.0-1    
 [22] textshaping_0.3.4    xfun_0.23            callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] polyclip_1.10-0      gtable_0.3.0         V8_3.4.2            
 [34] pkgbuild_1.2.0       abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] isoband_0.2.4        progress_1.2.2       viridisLite_0.4.0   
 [43] xtable_1.8-4         tmvnsim_1.0-2        stats4_4.1.0        
 [46] DT_0.18              httr_1.4.2           htmlwidgets_1.5.3   
 [49] threejs_0.3.3        RColorBrewer_1.1-2   ellipsis_0.3.2      
 [52] pkgconfig_2.0.3      loo_2.4.1            farver_2.1.0        
 [55] sass_0.4.0           here_1.0.1           utf8_1.2.1          
 [58] tidyselect_1.1.1     labeling_0.4.2       rlang_0.4.11        
 [61] reshape2_1.4.4       later_1.2.0          visNetwork_2.0.9    
 [64] munsell_0.5.0        cellranger_1.1.0     tools_4.1.0         
 [67] cli_2.5.0            generics_0.1.0       gifski_1.4.3-1      
 [70] ggridges_0.5.3       evaluate_0.14        stringr_1.4.0       
 [73] fastmap_1.1.0        yaml_2.2.1           ragg_1.1.2          
 [76] processx_3.5.2       knitr_1.33           purrr_0.3.4         
 [79] nlme_3.1-152         mime_0.10            projpred_2.0.2      
 [82] xml2_1.3.2           compiler_4.1.0       bayesplot_1.8.0     
 [85] shinythemes_1.2.0    rstudioapi_0.13      curl_4.3.1          
 [88] gamm4_0.2-6          png_0.1-7            tweenr_1.0.2        
 [91] bslib_0.2.5.1        stringi_1.6.2        highr_0.9           
 [94] ps_1.6.0             Brobdingnag_1.2-6    lattice_0.20-44     
 [97] Matrix_1.3-3         nloptr_1.2.2.2       markdown_1.1        
[100] shinyjs_2.0.0        vctrs_0.3.8          pillar_1.6.1        
[103] lifecycle_1.0.0      jquerylib_0.1.4      bridgesampling_1.1-2
[106] data.table_1.14.0    httpuv_1.6.1         R6_2.5.0            
[109] bookdown_0.22        promises_1.2.0.1     gridExtra_2.3       
[112] codetools_0.2-18     distill_1.2          boot_1.3-28         
[115] colourpicker_1.1.0   gtools_3.8.2         assertthat_0.2.1    
[118] rprojroot_2.0.2      withr_2.4.2          mnormt_2.0.2        
[121] shinystan_2.5.0      mgcv_1.8-35          parallel_4.1.0      
[124] hms_1.1.0            grid_4.1.0           tidyr_1.1.3         
[127] coda_0.19-4          minqa_1.2.4          rmarkdown_2.8       
[130] downlit_0.2.1        shiny_1.6.0          lubridate_1.7.10    
[133] base64enc_0.1-3      dygraphs_1.1.1.6    

---

1. o pacote bayesplot é automaticamente instalado como uma dependência do rstanarm ou brms então não se preocupe em instalá-lo. Ele será automaticamente instalado caso instale tanto rstanarm quanto brms.↩︎

2. lembrando que uma priori normal centrada em 0 por conta da simetria da normal também dá a possibilidade de valores negativos.↩︎

3. conseguimos fazer isso com distribuições normais por conta das diversas propriedades matemáticas destas distribuições. Note que isto não funciona para todas as diferentes distribuições.↩︎