Estatística Bayesiana com R e Stan: Priors

Jose Storopoli

A Estatística Bayesiana é caracterizada pelo uso de informação prévia embutida como probabilidade prévia $P(\theta)$, chamada de a priori¹:

\[ \underbrace{P(\theta \mid y)}_{\textit{Posteriori}} = \frac{\overbrace{P(y \mid \theta)}^{\text{Verossimilhança}} \cdot \overbrace{P(\theta)}^{\textit{Priori}}}{\underbrace{P(y)}_{\text{Constante Normalizadora}}}, \]

Subjetividade da Priori

Muitas críticas à estatística Bayesiana, se dá pela subjetividade da elucidação da probabilidade a priori de certas hipóteses ou parâmetros de modelos. A subjetividade é algo indesejado na idealização do cientista e do método científico. Ambos devem ser imparciais e guiados pelas evidências. Isto faz com que a objetividade seja o “Santo Graal” da ciência e do cientista. Vou falar uma coisa que talvez não tenha sido assimilada pelo leitor: tudo que envolve ação humana nunca será 100% objetivo. Temos subjetividade em tudo, e ciência não é um exceção².

O próprio processo dedutivo e criativo de formulação de teoria e hipóteses não é algo objetivo. Há muita subjetividade incorporada em novas proposições teóricas. A estatística frequentista, que bane o uso de probabilidades a priori³ também é subjetiva, pois há MUITA subjetividade em especificar um modelo e uma função de verossimilhança (Jaynes, 2003; van de Schoot et al., 2021). Ao fazermos isso, estamos inserindo pressupostos bem fortes e opinados sobre o processo de geração dos dados que estamos analisando. Isto quer dizer que, mesmo usando estatística frequentista, ainda sim estamos sendo bem subjetivos ao escolhermos como analisar os dados, pois muitas técnicas frequentistas possuem fortes pressupostos sobre os dados. Ainda mais, quando acoplamos esses pressupostos da estatística frequentista com a inexistência da elucidação desses pressupostos⁴ faz com que a idealização da objetividade da ciência e da estatística caiam por água baixo. Isto é um problema sério pois não é só a falha da objetividade, mas sim uma falha silenciosa e sorrateira. O véu de objetividade científica se desfaz e continuamos a acreditar que ele ainda está lá.

A estatística Bayesiana abraça a subjetividade enquanto a estatística frequentista a proíbe. Para a estatística Bayesiana, subjetividade guiam nossas inferências e nos levam a modelos mais robustos, confiáveis e que podem auxiliar à tomada de decisão. Já para a estatística frequentista, subjetividade é um tabu e todas inferências devem ser objetivas, mesmo que isso resulte em esconder pressupostos dos modelos embaixo dos panos. Consequentemente modelos oriundos da estatística frequentista, extremamente enviesados por pressupostos ocultos, não são robustos, podendo ser ilusórios e muitas vezes podem distorcer a realidade prejudicando o processo de tomada de decisão. Para concluir, estatística Bayesiana possui também pressupostos e subjetividade, mas estes são enunciados e formalizados. Ou seja, reconhecemos que a ação humana, mesmo em cenários científicos, é subjetiva e toda a subjetividade e os pressupostos do modelo são expostos de maneira transparente e auditável. Para mim isto faz toda diferença, uma vez que podemos desacoplar fatos de opinião e discutí-los separadamente ou de maneira conjunta.

Portanto, caro leitor, abrace a incerteza e subjetividade, mas nunca esconda-a e sempre deixe-as à vista de maneira transparente e auditável.

Tipos de Prioris

De maneira geral, podemos ter 3 tipos de priori em uma abordagem Bayesiana (Gelman et al., 2013; McElreath, 2020; van de Schoot et al., 2021):

uniforme (flat): não recomendada
fracamente informativa (weakly informative): pequena restrição com um pouco de senso comum e baixo conhecimento de domínio incorporado
informativa (informative): conhecimento de domínio incorporado

Para se aprofundar mais recomendo a vinheta do rstanarm sobre prioris.

Prioris para os Modelos `rstanarm`

O rstanarm possui as seguintes prioris incorporadas como padrão nos seus modelos. Recomendo fortemente que você use uma priori específica e não se atenha às prioris padrões do rstanarm. Apesar de refletirem as boas práticas e a fronteira do conhecimento científico sobre elucidação de prioris, elas podem mudar conforme são lançadas novas versões do rstanarm ou são incorporados novas diretrizes de elucidação de prioris. Isto pode prejudicar a robustez do seu modelo (e em especial do seu código), pois caso executado com versões diferentes do rstanarm, a opção de prioris padrão pode levar à diferentes elucidações de prioris.

Argumento	Usado em	Aplica-se à
`prior_intercept`	Todas funções de modelagem exceto `stan_polr` and `stan_nlmer`	Constante (intercept) do modelo, após centralização dos preditores
`prior`	Todas funções de modelagem	Coeficientes de Regressão, não inclui coeficientes que variam por grupo em modelos multiníveis (veja `prior_covariance`)
`prior_aux`	`stan_glm`, `stan_glmer`, `stan_gamm4`, `stan_nlmer`	Parâmetro auxiliar (ex: desvio padrão (standard error – DP), interpretação depende do modelo
`prior_covariance`	`stan_glmer`, `stan_gamm4`, `stan_nlmer`	Matrizes de covariância em modelos multiníveis

Uniforme (flat)

Especifica-se colocando o valor NULL (nulo em R) nos argumentos prior_* dos modelos rstanarm. Exemplo:

prior_intercept = NULL – constante possuirá priori uniforme sobre todos os números reais $(-\infty, +\infty)$
prior = NULL – parâmetros possuirão prioris uniformes sobre todo os números reais $(-\infty, +\infty)$
prior_aux = NULL – parâmetros auxiliares (geralmente o erro do modelo) possuirão prioris uniforme sobre todos os números reais $(-\infty, +\infty)$. No caso de erro do modelo, isto se restringe aos numeros reais positivos: $[0, +\infty)$

Colocando na função de modelo ficaria:

fit <- stan_glm(y ~ ...,
  prior = NULL,
  prior_intercept = NULL,
  prior_aux = NULL)

Informativas

Coloca-se qualquer distribuição nos argumentos. Exemplo:

prior = normal(0, 5) – $\text{Normal}(0, 5)$
prior_intercept = student_t(4, 0, 10) – $\text{Student}(\nu = 4, 0, 10)$
prior_aux = cauchy(0, 3) – $\text{Cauchy}^+(0, 3)$⁵

Colocando na função de modelo ficaria:

fit <- stan_glm(y ~ ...,
  prior = normal(0, 5),
  prior_intercept = student_t(4, 0, 10),
  prior_aux = cauchy(0, 3))

Padrões do `rstanarm`

Acontece se você não especifica nada nos argumentos prior* do rstanarm, os comportamentos diferem conforme o modelo. Aqui divido em modelos gaussianos (família de função verossimilhança Gaussiana ou normal) e outros (famílias de funções de verossimilhança binomial, poisson, etc…)

Modelos Gaussianos

Constante (Intercept): Normal centralizada com média $\mu_y$ e desvio padrão de $2.5 \sigma_y$ - prior_intercept = normal(mean_y, 2.5 * sd_y)
Coeficientes: Normal para cada coeficiente média $\mu = 0$ e desvio padrão de $2.5\times\frac{\sigma_y}{\sigma_{x_k}}$ - prior = normal(0, 2.5 * sd_y/sd_xk)

Em notação matemática:

\[ \begin{aligned} \alpha &\sim \text{Normal}(\mu_y, 2.5 \cdot \sigma_y)\\ \beta_k &\sim \text{Normal}\left( 0, 2.5 \cdot \frac{\sigma_y}{\sigma_{x_k}} \right) \\ \sigma &\sim \text{Exponential}\left( \frac{1}{\sigma_y} \right) \end{aligned} \]

Outros Modelos (Binomial, Poisson etc.)

Constante (Intercept): Normal centralizada com média $\mu = 0$ e desvio padrão de $2.5 \sigma_y$ - prior_intercept = normal(0, 2.5 * sd_y)
Coeficientes: Normal para cada coeficiente média $\mu = 0$ e desvio padrão de $2.5\times\frac{1}{\sigma_{x_k}}$ - prior = normal(0, 2.5 * 1/sd_xk)

OBS: em todos os modelos prior_aux, o desvio padrão do erro do modelo, a priori padrão é uma distribuição exponencial com taxa $\frac{1}{\sigma_y}$: prior_aux = exponential(1/sd_y).

Em notação matemática:

\[ \begin{aligned} \alpha &\sim \text{Normal}(0, 2.5 \cdot \sigma_y)\\ \beta_k &\sim \text{Normal}\left( 0, 2.5 \cdot \frac{1}{\sigma_{x_k}} \right) \\ \sigma &\sim \text{Exponential}\left( \frac{1}{\sigma_y} \right) \end{aligned} \]

Padrões do `brms`

Como o brms dá muito mais autonomia, poder e flexibilidade ao usuário, todas as prioris padrões dos coeficientes dos modelos são literalmente prioris uniformes sobre todo os números reais $(-\infty, +\infty)$. brms apenas ajusta de maneira robusta a priori para:

Constante (Intercept): $t$ de Student média $\mu = \text{mediana}(y)$, desvio padrão de $\text{MAD}(y)$ e graus de liberdade $\nu = 3$
Erro (sigma): $t$ de Student média $\mu = 0$ e desvio padrão de $\text{MAD}(y)$

OBS: $\text{MAD}$ quer dizer Mean Absolute Deviation – Desvio Absoluto Médio.

Em notação matemática:

\[ \begin{aligned} \alpha &\sim \text{Student}(\nu = 3, \text{mediana}(y), \text{MAD}(y) )\\ \beta_k &\sim \text{Unif}(- \infty, + \infty) \\ \sigma &\sim \text{Student}(\nu = 3, 0, \text{MAD}(y) ) \end{aligned} \]

Por isso recomendo fortemente você especificar suas próprias prioris em todos os modelos brms. Para especificar uma priori no brms, use o argumento prior com o valor prior(). Exemplo de uma priori especificada como $\text{Normal}(0, 10)$ para todos os coeficientes $\beta$ do modelo (b):

brms_fit <- brm(y ~ ..., prior = prior(normal(0, 10), class = b))

Exemplo usando o `mtcars` com `rstanarm`

Vamos estimar modelos Bayesianos usando o dataset já conhecido mtcars da Aula 1 - Comandos Básicos de R. A idéia é usarmos como variável dependente a autonomia do carro (milhas por galão – mpg) e como independentes o peso do carro (wt) e se o carro é automático ou manual (am). A fórmula então fica:

mpg ~ wt + am

Para constar, calcularemos alguns valores antes de ver o sumário das prioris:

$\mu_y$: média do mpg - 20.09
$2.5 \sigma_y$: 2.5 * sd(mtcars$mpg) - 15.07
$2.5 \times \frac{\sigma_y}{\sigma_{x_{\text{wt}}}}$: 2.5 * (sd(mtcars$mpg) / sd(mtcars$wt)) - 15.4
$2.5\ times \frac{\sigma_y}{\sigma_{x_{\text{am}}}}$: 2.5 * (sd(mtcars$mpg) / sd(mtcars$am)) - 30.2
$\frac{1}{\sigma_y}$: 1 / sd(mtcars$mpg) - 0.17

A função prior_summary() do rstanarm resulta um sumário conciso das prioris utilizadas em um modelo. Coloque como argumento o modelo estimado:

library(rstanarm)
rstanarm_default_prior <- stan_glm(mpg ~ wt + am, data = mtcars, chains = 1)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 0.00015 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 1.5 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.053396 seconds (Warm-up)
Chain 1:                0.053265 seconds (Sampling)
Chain 1:                0.106661 seconds (Total)
Chain 1:

prior_summary(rstanarm_default_prior)

Priors for model 'rstanarm_default_prior' 
------
Intercept (after predictors centered)
  Specified prior:
    ~ normal(location = 20, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 20, scale = 15)

Coefficients
  Specified prior:
    ~ normal(location = [0,0], scale = [2.5,2.5])
  Adjusted prior:
    ~ normal(location = [0,0], scale = [15.40,30.20])

Auxiliary (sigma)
  Specified prior:
    ~ exponential(rate = 1)
  Adjusted prior:
    ~ exponential(rate = 0.17)
------
See help('prior_summary.stanreg') for more details

Agora com prioris especificadas:

Como há dois coeficientes eu especifico médias iguais ($0$), porém desvios padrões diferentes ($5$ para wt e $6$ para am) usando a função de combinar do R (combine) - c():

rstanarm_custom_prior <- stan_glm(mpg ~ wt + am, data = mtcars, chains = 1,
         prior = normal(c(0, 0), c(5, 6)),
         prior_intercept = student_t(4, 0, 10),
         prior_aux = cauchy(0, 3))


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.9e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.19 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.039979 seconds (Warm-up)
Chain 1:                0.046262 seconds (Sampling)
Chain 1:                0.086241 seconds (Total)
Chain 1:

prior_summary(rstanarm_custom_prior)

Priors for model 'rstanarm_custom_prior' 
------
Intercept (after predictors centered)
 ~ student_t(df = 4, location = 0, scale = 10)

Coefficients
 ~ normal(location = [0,0], scale = [5,6])

Auxiliary (sigma)
 ~ half-cauchy(location = 0, scale = 3)
------
See help('prior_summary.stanreg') for more details

Exemplo usando o `mtcars` com `brms`

Vamos usar o mesmo modelo que usamos para o rstanarm acima. Note que a fórmula não muda e usaremos a mesma:

mpg ~ wt + am

A função prior_summary() do brms resulta um sumário conciso das prioris utilizadas em um modelo. Coloque como argumento o modelo estimado:

library(brms)
brms_default_prior <- brm(mpg ~ wt + am, data = mtcars, chains = 1)


SAMPLING FOR MODEL '5c829c9ee139a11d74ba6f4816e16620' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.7e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.019722 seconds (Warm-up)
Chain 1:                0.01533 seconds (Sampling)
Chain 1:                0.035052 seconds (Total)
Chain 1:

prior_summary(brms_default_prior)

                   prior     class coef group resp dpar nlpar bound
                  (flat)         b                                 
                  (flat)         b   am                            
                  (flat)         b   wt                            
 student_t(3, 19.2, 5.4) Intercept                                 
    student_t(3, 0, 5.4)     sigma                                 
       source
      default
 (vectorized)
 (vectorized)
      default
      default

Agora com prioris especificadas:

Aqui nos agrupamos todas as prioris com o argumento prior e usando a função de combinar do R (combine) - c():

brms_custom_prior <- brm(mpg ~ wt + am, data = mtcars, chains = 1,
         prior = c(
           prior(normal(0, 5), class = b, coef = wt),
           prior(normal(0, 6), class = b, coef = am),
           prior(student_t(4, 0, 10), class = Intercept),
           prior(cauchy(0, 3), class = sigma)
         ))


SAMPLING FOR MODEL 'f73c349d97a4380ebf93fa375a214f2e' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.7e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.17 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.020771 seconds (Warm-up)
Chain 1:                0.015114 seconds (Sampling)
Chain 1:                0.035885 seconds (Total)
Chain 1:

prior_summary(brms_custom_prior)

               prior     class coef group resp dpar nlpar bound
              (flat)         b                                 
        normal(0, 6)         b   am                            
        normal(0, 5)         b   wt                            
 student_t(4, 0, 10) Intercept                                 
        cauchy(0, 3)     sigma                                 
  source
 default
    user
    user
    user
    user

Por quê não é interessante usar prioris uniformes (flat priors)

Uma priori totalmente uniforme ou chapada (flat) é algo que devemos evitar (Gelman et al., 2013; van de Schoot et al., 2021) pelo simples motivo que ela parte da premissa de que “tudo é possível.” Não há limites na crença de que tamanho o valor deve ser ou quaisquer restrições.

Prioris chapadas e super-vagas geralmente não são recomendadas e algum esforço deve ser incluído para ter, pelo menos, prioris um pouco informativas. Por exemplo, é comum esperar que os tamanhos de efeito realistas sejam da ordem de magnitude $0.1$ em uma escala padronizada (por exemplo, uma inovação educacional que pode melhorar as pontuações dos testes em $0.1$ desvios padrão). Nesse caso, uma priori de $\text{Normal} (0,1)$ poderia ser considerado muito informativo, de uma maneira ruim, pois coloca a maior parte de sua massa em valores de parâmetro que são irrealisticamente grandes em valor absoluto. O ponto geral aqui é que se considerarmos uma priori como “fraca” ou “forte,” isso é uma propriedade não apenas da priori, mas também da pergunta que está sendo feita.

Quando dizemos que a priori é “pouco informativa,” o que queremos dizer é que, se houver uma quantidade razoavelmente grande de dados, a likelihood dominará e a priori não será importante. Se os dados forem fracos, porém, esta “priori fracamente informativo” influenciará fortemente a inferência posterior.

Um outro exemplo interessante vem de uma aula do Ben Goodrich ⁶ professor de Columbia e membro do grupo de pesquisa de Stan. Aqui ele fala sobre um dos maiores efeitos observados nas ciências sociais. Nas pesquisas de intenção de voto à eleição presidencial dos EUA de 2008 (Obama vs McCain), se você trocasse a raça de um respondente de race_black = 0 para race_black = 1 isso gerava um aumento de aproximadamente 60% (0.6) na probabilidade do respondente votar no Obama. Em escala logit esses 60% se traduziriam em um modelo binomial como um coeficiente $\beta_{\text{Race Black}} = 4.5$. Esse tamanho de efeito (um dos maiores observados na história das ciências sociais) seria facilmente inferido com a prior padrão do rstanarm para modelos binomiais: $\beta_{\text{Race Black}} \sim \text{Normal}\left( 0, 2.5 \cdot \frac{1}{\sigma_{\text{Race Black}}} \right)$.

Por fim, não se esqueça que muitas distribuições, como por exemplo a distribuição normal, possuem suporte $\mathbb{R}$, ou seja pode acontecer qualquer número entre $-\infty$ até $\infty$ independente da média $\mu$ ou desvio padrão $\sigma$. É claro que moralmente a probabilidade $P(X = 100)$ para $X \sim \text{Normal}(0, 0.01)$ é zero, mesmo que matematicamente seja uma quantidade muito pequena $\epsilon$.

Bayesian Workflow

O fluxo de trabalho que fazemos quando especificamos e executamos amostragem de modelos Bayesianos não é linear ou acíclico (Gelman et al., 2020). Isto quer dizer que precisamos iterar (ir e voltar) diversas vezes entre as diferentes etapas. A figura 1 demonstra o fluxo de trabalho⁷:

Figure 1: Bayesian Workflow. Baseado em Gelman et al. (2020)

Prior Predictive Check

Em especial, antes de começar a alimentar o modelo com dados precisamos fazer uma checagem de todas as nossas prioris. Isso é chamado de Prior Predictive Check. De maneira muito simples, consiste em simular parâmetros com base nas suas distribuições especificadas a priori no modelo sem qualquer condicionamento aos dados e sem envolvimento nenhum da função de verossimilhança. Independentemente do nível de informação especificada na priori, é sempre importante realizar uma análise de sensibilidade prévia para entender completamente a influência que as prioris têm na posterior.

Isso pode ser feito tanto no rstanarm quando no brms:

rstanarm: em qualquer função stan_*() usar o argumento prior_PD = TRUE
brms: na função brm() usar o argumento sample_prior = "only"

Exemplo `rstanarm`

Continuando no nosso exemplo mtcars da Aula 1 - Comandos Básicos de R:

rstanarm_custom_prior <- stan_glm(mpg ~ wt + am, data = mtcars, chains = 1,
         prior = normal(c(0, 0), c(5, 6)),
         prior_intercept = student_t(4, 0, 10),
         prior_aux = cauchy(0, 3),
         prior_PD = TRUE)


SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 2e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.2 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.027839 seconds (Warm-up)
Chain 1:                0.026168 seconds (Sampling)
Chain 1:                0.054007 seconds (Total)
Chain 1:

summary(rstanarm_custom_prior)


Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      mpg ~ wt + am
 algorithm:    sampling
 sample:       1000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 32
 predictors:   3

Estimates:
              mean   sd    10%   50%   90%
(Intercept)   0.9   21.2 -24.7   0.3  27.2
wt           -0.1    4.9  -6.2   0.2   6.2
am            0.0    6.1  -7.6  -0.1   7.7
sigma        15.4   82.2   0.5   3.1  20.5

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.7  1.0   830 
wt            0.2  1.0   839 
am            0.2  1.0  1013 
sigma         2.9  1.0   799 
log-posterior 0.1  1.0   367 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

O foco é verificar se os valores dos parâmetros de interesse amostrados apenas das prioris fazem sentido. Por exemplo uma constante (intercept) com 90% de densidade entre -24.5 e 26.0 não faz sentido. Talvez seja melhor especificarmos uma priori um pouco mais informada.

Exemplo `brms`

Continuando no nosso exemplo mtcars da Aula 1 - Comandos Básicos de R:

brms_custom_prior <- brm(mpg ~ wt + am, data = mtcars, chains = 1,
         prior = c(
           prior(normal(0, 5), class = b, coef = wt),
           prior(normal(0, 6), class = b, coef = am),
           prior(student_t(4, 0, 10), class = Intercept),
           prior(cauchy(0, 3), class = sigma)
         ),
         sample_prior = "only")


SAMPLING FOR MODEL 'f73c349d97a4380ebf93fa375a214f2e' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.2e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.014857 seconds (Warm-up)
Chain 1:                0.010824 seconds (Sampling)
Chain 1:                0.025681 seconds (Total)
Chain 1:

summary(brms_custom_prior)

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: mpg ~ wt + am 
   Data: mtcars (Number of observations: 32) 
Samples: 1 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 1000

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept     1.51     20.52   -38.60    42.09 1.00      717      656
wt           -0.36      4.91    -9.78     9.06 1.00      735      633
am            0.10      6.08   -11.30    11.68 1.00      961      685

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma    13.87     91.04     0.07    72.66 1.00     1052      490

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

O interessante do brms é que conseguimos naturalmente visualizar hipóteses sobre os valores do parâmetros de modelos estimados pela função brm(). Veja um exemplo na figura 2 com o método plot() da função hypothesis():

plot(hypothesis(brms_custom_prior, "Intercept = 0"))

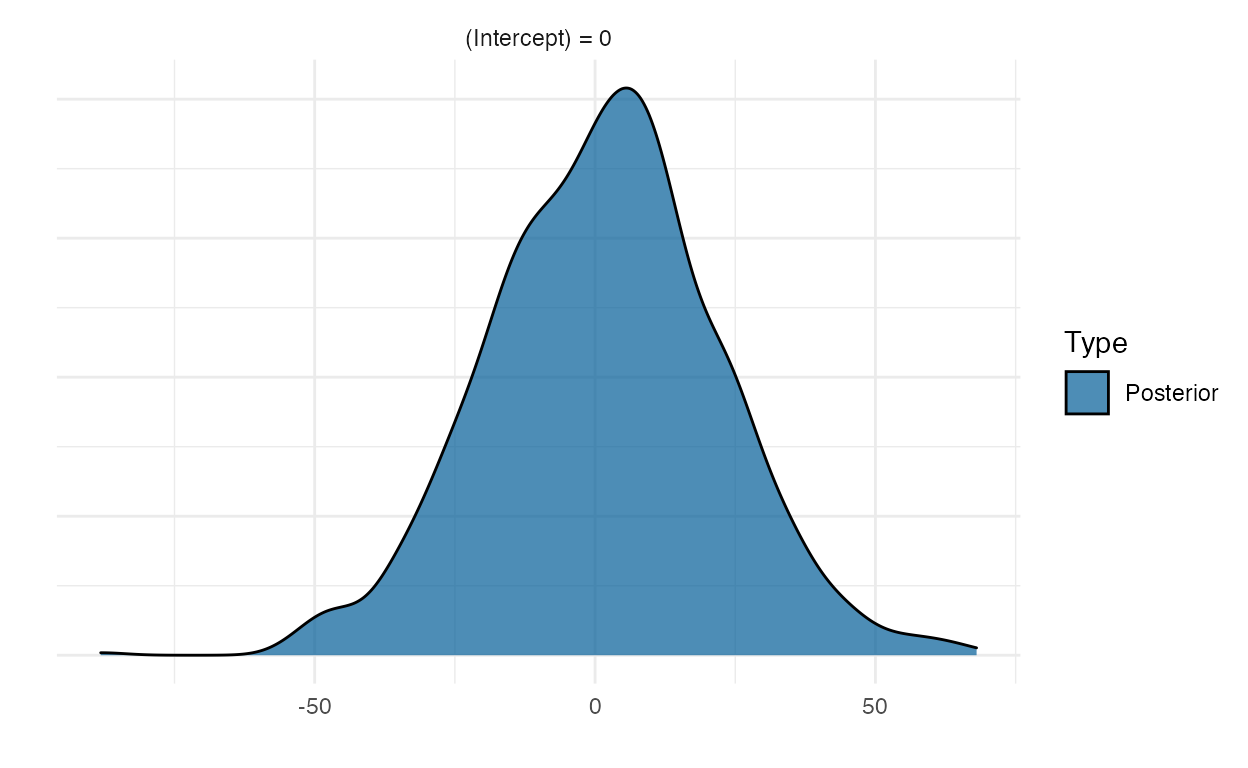
Figure 2: Função hypothesis() do brms

Atividade Prática

Regressão linear especificando prioris fracamente informativas. Usar o dataset do pacote carData chamado Salaries

library(carData)
data("Salaries")
?Salaries

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] carData_3.0-4      DiagrammeR_1.0.6.1 brms_2.15.0       
 [4] rstanarm_2.21.1    Rcpp_1.0.6         skimr_2.1.3       
 [7] readr_1.4.0        readxl_1.3.1       tibble_3.1.2      
[10] ggplot2_3.3.3      patchwork_1.1.1    cowplot_1.1.1     

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         repr_1.1.3           splines_4.1.0       
  [7] crosstalk_1.1.1      rstantools_2.1.1     inline_0.3.19       
 [10] digest_0.6.27        htmltools_0.5.1.1    magick_2.7.2        
 [13] rsconnect_0.8.18     fansi_0.5.0          magrittr_2.0.1      
 [16] RcppParallel_5.1.4   matrixStats_0.59.0   xts_0.12.1          
 [19] prettyunits_1.1.1    colorspace_2.0-1     textshaping_0.3.4   
 [22] xfun_0.23            dplyr_1.0.6          callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] gtable_0.3.0         V8_3.4.2             pkgbuild_1.2.0      
 [34] rstan_2.21.2         abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] xtable_1.8-4         stats4_4.1.0         StanHeaders_2.21.0-7
 [43] DT_0.18              htmlwidgets_1.5.3    threejs_0.3.3       
 [46] RColorBrewer_1.1-2   ellipsis_0.3.2       pkgconfig_2.0.3     
 [49] loo_2.4.1            farver_2.1.0         sass_0.4.0          
 [52] utf8_1.2.1           tidyselect_1.1.1     labeling_0.4.2      
 [55] rlang_0.4.11         reshape2_1.4.4       later_1.2.0         
 [58] visNetwork_2.0.9     munsell_0.5.0        cellranger_1.1.0    
 [61] tools_4.1.0          cli_2.5.0            generics_0.1.0      
 [64] ggridges_0.5.3       evaluate_0.14        stringr_1.4.0       
 [67] fastmap_1.1.0        yaml_2.2.1           ragg_1.1.2          
 [70] processx_3.5.2       knitr_1.33           purrr_0.3.4         
 [73] nlme_3.1-152         mime_0.10            projpred_2.0.2      
 [76] xml2_1.3.2           compiler_4.1.0       bayesplot_1.8.0     
 [79] shinythemes_1.2.0    rstudioapi_0.13      curl_4.3.1          
 [82] gamm4_0.2-6          png_0.1-7            bslib_0.2.5.1       
 [85] stringi_1.6.2        highr_0.9            ps_1.6.0            
 [88] Brobdingnag_1.2-6    lattice_0.20-44      Matrix_1.3-3        
 [91] nloptr_1.2.2.2       markdown_1.1         shinyjs_2.0.0       
 [94] vctrs_0.3.8          pillar_1.6.1         lifecycle_1.0.0     
 [97] jquerylib_0.1.4      bridgesampling_1.1-2 httpuv_1.6.1        
[100] R6_2.5.0             bookdown_0.22        promises_1.2.0.1    
[103] gridExtra_2.3        codetools_0.2-18     distill_1.2         
[106] boot_1.3-28          colourpicker_1.1.0   MASS_7.3-54         
[109] gtools_3.8.2         assertthat_0.2.1     rprojroot_2.0.2     
[112] withr_2.4.2          shinystan_2.5.0      mgcv_1.8-35         
[115] parallel_4.1.0       hms_1.1.0            grid_4.1.0          
[118] tidyr_1.1.3          coda_0.19-4          minqa_1.2.4         
[121] rmarkdown_2.8        downlit_0.2.1        shiny_1.6.0         
[124] lubridate_1.7.10     base64enc_0.1-3      dygraphs_1.1.1.6

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis. Chapman and Hall/CRC.

Gelman, A., Vehtari, A., Simpson, D., Margossian, C. C., Carpenter, B., Yao, Y., … Modr’ak, M. (2020, November 3). Bayesian Workflow. Retrieved February 4, 2021, from http://arxiv.org/abs/2011.01808

Jaynes, E. T. (2003). Probability theory: The logic of science. Cambridge university press.

McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan. CRC press.

van de Schoot, R., Depaoli, S., King, R., Kramer, B., Märtens, K., Tadesse, M. G., … Yau, C. (2021). Bayesian statistics and modelling. Nature Reviews Methods Primers, 1(1, 1), 1–26. https://doi.org/10.1038/s43586-020-00001-2

também há o termo em inglês: prior.↩︎
caso discorde, dê uma estudada no rico campo da economia comportamental que provém uma montanha de evidências que os seres humanos são extremamente suscetíveis à vieses e, de maneira geral, não são bons tomadores de decisão.↩︎
lembrando que sob a tutela da estatística frequentista, estamos proibidos de conjecturar probabilidade de parâmetros, pois eles são fixos e dependem apenas dos dados que temos. O que é conjecturado probabilisticamente são os dados em sí: a inferência é sempre elaborada a partir de um processo de frequência na qual há o pressuposto de “amostragem de $N$ amostras de uma mesma população” no limite de $N \to \infty$.↩︎
veja que muitas disciplinas de estatística nem mencionam pressupostos das diferentes técnicas frequentistas.↩︎
A distribuição Cauchy é o caso especial de uma distribuição $t$ de Student com 1 grau de liberdade $( \eta = 1)$. Note que como ela é especificada como uma priori de um parâmetro auxiliar (no caso o erro do modelo), ela somente tomará valores positivos por isso o $\text{Cauchy}^+$.↩︎
caso queira ver o vídeo na íntegra, a parte que nos interessa de prioris começa a partir do minuto 40↩︎
note que o fluxo está extremamente simplificado do fluxo original no qual foi baseado. Sugiro o leitor consultar o fluxo original de Gelman et al. (2020).↩︎

Priors

Subjetividade da Priori

Tipos de Prioris

Prioris para os Modelos `rstanarm`

Uniforme (flat)

Informativas

Padrões do `rstanarm`

Modelos Gaussianos

Outros Modelos (Binomial, Poisson etc.)

Padrões do `brms`

Exemplo usando o `mtcars` com `rstanarm`

Exemplo usando o `mtcars` com `brms`

Por quê não é interessante usar prioris uniformes (flat priors)

Bayesian Workflow

Prior Predictive Check

Exemplo `rstanarm`

Exemplo `brms`

Atividade Prática

Ambiente

References

Corrections

Reuse

Citation

Priors

Subjetividade da Priori

Tipos de Prioris

Prioris para os Modelos rstanarm

Uniforme (flat)

Informativas

Padrões do rstanarm

Modelos Gaussianos

Outros Modelos (Binomial, Poisson etc.)

Padrões do brms

Exemplo usando o mtcars com rstanarm

Exemplo usando o mtcars com brms

Por quê não é interessante usar prioris uniformes (flat priors)

Bayesian Workflow

Prior Predictive Check

Exemplo rstanarm

Exemplo brms

Atividade Prática

Ambiente

References

Corrections

Reuse

Citation

Prioris para os Modelos `rstanarm`

Padrões do `rstanarm`

Padrões do `brms`

Exemplo usando o `mtcars` com `rstanarm`

Exemplo usando o `mtcars` com `brms`

Exemplo `rstanarm`

Exemplo `brms`