Saindo do universo dos modelos lineares, começamos a nos aventurar nos modelos linares generalizados (generalized linear models - GLM). O segundo deles é a regressão de Poisson.
Uma regressão de Poisson se comporta exatamente como um modelo linear: faz uma predição simplesmente computando uma soma ponderada das variáveis independentes \(\mathbf{X}\) pelos coeficientes estimados \(\boldsymbol{\beta}\), mais uma constante \(\alpha\). Porém ao invés de retornar um valor contínuo \(\boldsymbol{y}\), como a regressão linear, retorna o logarítmo natural desse valor:
\[ \log(\boldsymbol{y})= \alpha \cdot \beta_1 x_1 \cdot \beta_2 x_2 \cdot \ldots \cdot \beta_k x_k \]
que é o mesmo que:
\[ \boldsymbol{y} = e^{(\alpha + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_k x_k)} \]
- \(\boldsymbol{\theta} \in \mathbb{R}^p\) - parâmetros do modelo
- \(\theta_0\) - constante
- \(\theta_1, \theta_2, \dots, \theta_p\) - coeficientes das variáveis independentes \(x_1, x_2, \dots, p\)
- \(n\) - número de variáveis independentes
A função \(e^x\) é chamada de função exponencial. Veja a figura 1 para uma intuição gráfica da função exponencial:
ggplot(data = tibble(
x = seq(0, 10, length.out = 100),
y = exp(x)
),
aes(x, y)) +
geom_line(size = 2, color = "steelblue") +
ylab("Exponencial(x)")
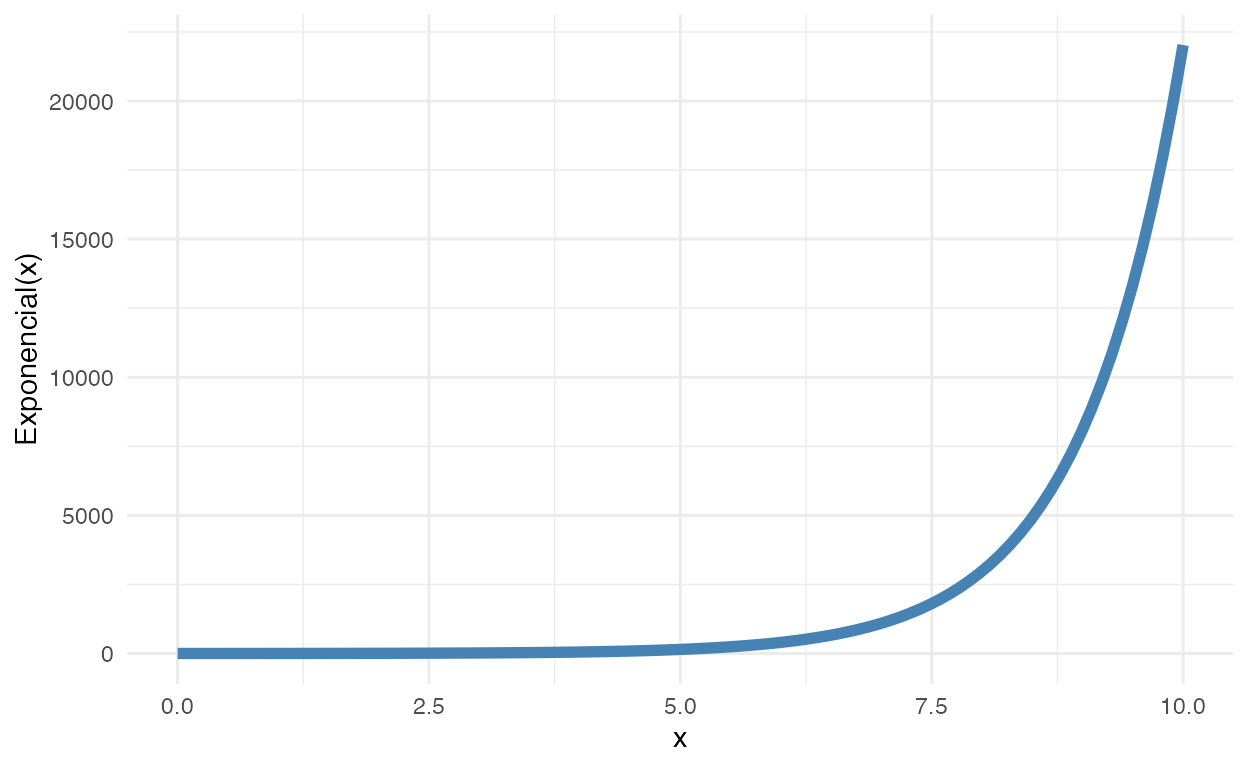
Figure 1: Função Exponencial
Regressão de Poisson é usada quando a nossa variável dependente só pode tomar valores positivos, geralmente em contextos de dados de contagem.
Regressão de Poisson Bayesiana
Podemos fazer uma regressão de Poisson se a variável dependente \(\boldsymbol{y}\) for uma variável com dados de contagem, ou seja, \(\boldsymbol{y}\) somente toma valores positivos. A função de verossimilhança de Poisson usa uma constante \(\alpha\) e os coeficientes \(\boldsymbol{\beta}\) porém estes são exponenciados (\(e^x\)):
\[ \begin{aligned} \boldsymbol{y} &\sim \text{Poisson}\left( e^{(\alpha + \mathbf{X} \boldsymbol{\beta})} \right) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \end{aligned} \]
Como podemos ver, o preditor linear \(\alpha + \mathbf{X} \boldsymbol{\beta}\) é o logaritmo do valor de \(\boldsymbol{y}\). Portanto precisamos exponenciar os valores do preditor linear:
\[ \begin{aligned} \log(y) &= \alpha + \mathbf{X} \boldsymbol{\beta} \\ \boldsymbol{y} &= e^{ \left( \alpha + \mathbf{X} \boldsymbol{\beta} \right) } \\ \boldsymbol{y} &= e^{\alpha} \cdot e^{\left( \mathbf{X} \boldsymbol{\beta} \right)} \end{aligned} \]
A constante \(\alpha\) e os coeficientes \(\boldsymbol{\beta}\) são apenas interpretados após a exponenciação.
Regressão de Poisson com o rstanarm e brms
O rstanarm e brms podem tolerar qualquer modelo linear generalizado e regressão de Poisson não é uma exceção. Para designar um modelo de Poisson no rstanarm e brms é preciso simplesmente alterar o argumento family da função stan_glm() ou brm(). Isso faz com que a família da função de verossimilhança do modelo seja modificada. Você pode controlar também a função de ligação com argumento link mas acredito que para a vasta maioria dos casos não é necessário alterar o padrão que Stan usa para as diferentes famílias de funções de verossimilhança.
Exemplo Poisson - Exterminação de baratas
Para exemplo, usaremos um dataset chamado roaches (Gelman & Hill, 2007) que está incluído no rstanarm. É uma base de dados com 262 observações sobre a eficácia de um sistema de controle de pragas em reduzir o número de baratas (roaches) em apartamentos urbanos.
Possui as seguintes variáveis:
y: variável dependente - número de baratas mortasroach1: número de baratas antes da dedetizaçãotreatment: dummy para indicar se o apartamento foi dedetizado ou nãosenior: dummy para indicar se há apenas idosos no apartamentoexposure2: número de dias que as armadilhas de baratas foram usadas
# Detectar quantos cores/processadores
options(mc.cores = parallel::detectCores())
options(Ncpus = parallel::detectCores())
library(rstanarm)
data(roaches)
Descritivo das variáveis
Antes de tudo, analise SEMPRE os dados em mãos. Graficamente e com tabelas. Isso pode ajudar a elucidar prioris além de embasar melhor conhecimento de domínio do fenômeno de interesse.
Pessoalmente uso o pacote skimr (Waring et al., 2021) com a função skim():
| Name | roaches |
| Number of rows | 262 |
| Number of columns | 5 |
| _______________________ | |
| Column type frequency: | |
| numeric | 5 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 0 | 1 | 25.65 | 50.85 | 0.0 | 0 | 3 | 24 | 357.0 | ▇▁▁▁▁ |
| roach1 | 0 | 1 | 42.19 | 75.26 | 0.0 | 1 | 7 | 50 | 450.0 | ▇▁▁▁▁ |
| treatment | 0 | 1 | 0.60 | 0.49 | 0.0 | 0 | 1 | 1 | 1.0 | ▅▁▁▁▇ |
| senior | 0 | 1 | 0.31 | 0.46 | 0.0 | 0 | 0 | 1 | 1.0 | ▇▁▁▁▃ |
| exposure2 | 0 | 1 | 1.02 | 0.32 | 0.2 | 1 | 1 | 1 | 4.3 | ▇▂▁▁▁ |
Modelo de Poisson
O modelo possuirá as seguintes variáveis como independentes: roach1, treatment e senior. Para todas essas variáveis, como os coeficientes estarão em um escala logarítma usarei uma priori de uma distribuição normal com média 0 e os respectivos desvios padrões de 0.1, 5 e 51. O que resulta em prior = normal(c(0, 0, 0), c(0.1, 5, 5)). Vou colocar a priori da constante \(\alpha\) como uma normal centrada em 0 e com um desvio padrão 2.5, basicamente traduzindo o que usamos como priori em modelos gaussianos (regressão linear). Isto resulta em prior_intercept = normal(0, 2.5). Notem que aqui não temos erro do modelo, pois a função de verossimilhança não faz pressupostos sobre desvios como era o caso na regressão linear com uma verossimilhança Gaussiana/Normal. Portanto não há o que se especificar para prior_aux.
Vamos ver como ficaram as estimação dos parâmetros de interesse do modelo com summary():
summary(model_poisson)
Model Info:
function: stan_glm
family: poisson [log]
formula: y ~ roach1 + treatment + senior
algorithm: sampling
sample: 4000 (posterior sample size)
priors: see help('prior_summary')
observations: 262
predictors: 4
Estimates:
mean sd 10% 50% 90%
(Intercept) 3.1 0.0 3.1 3.1 3.2
roach1 0.0 0.0 0.0 0.0 0.0
treatment -0.5 0.0 -0.5 -0.5 -0.5
senior -0.4 0.0 -0.4 -0.4 -0.3
Fit Diagnostics:
mean sd 10% 50% 90%
mean_PPD 25.6 0.4 25.1 25.6 26.2
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.0 1.0 3177
roach1 0.0 1.0 3559
treatment 0.0 1.0 2753
senior 0.0 1.0 2636
mean_PPD 0.0 1.0 3230
log-posterior 0.0 1.0 1559
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).Não tivemos nenhum problema nas correntes Markov pois todos os Rhat estão bem abaixo de 1.01.
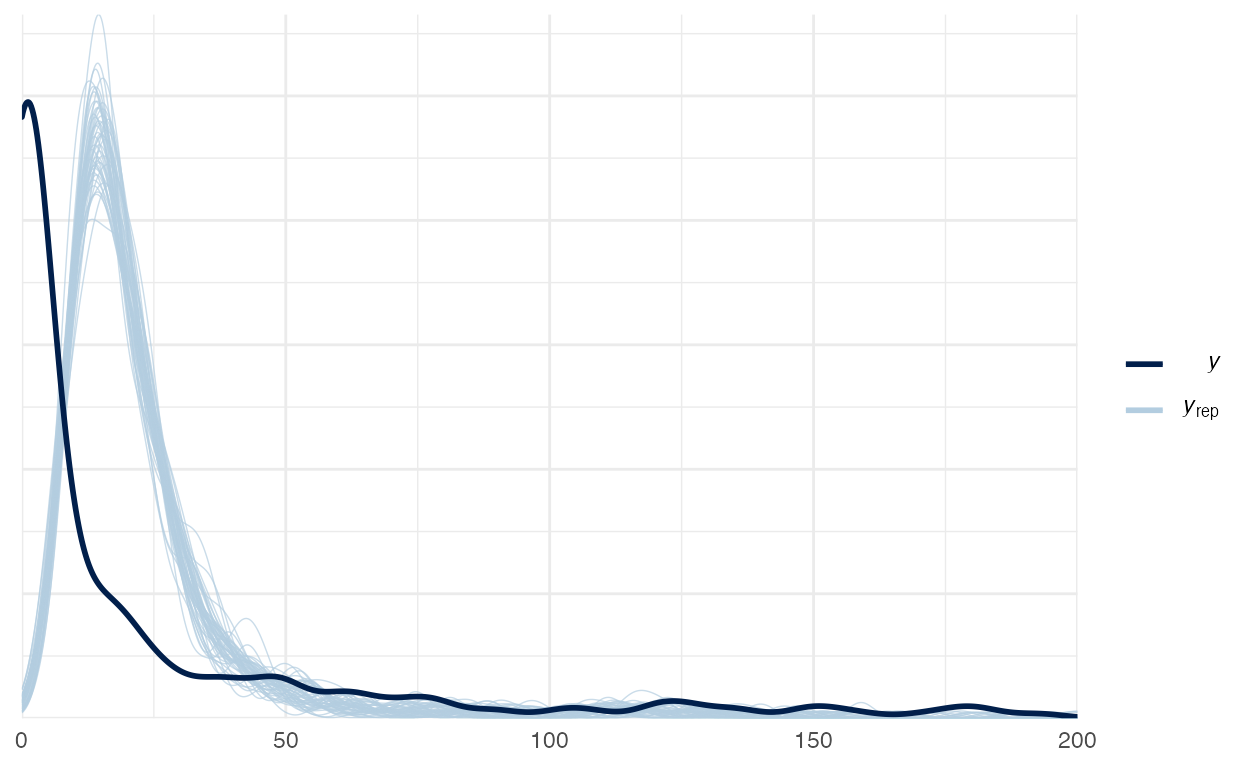
Vamos verificar o Posterior Predictive Check do modelo de Poisson na figura 2:
Este é um bom exemplo de um Posterior Predictive Check no qual há algo errado com o modelo. Isto indica que devemos pensar melhor nas variáveis nas prioris, ou até incorporar mais variáveis no modelo. A função de verossimilhança faz um bom trabalho em se moldar à densidade da variável dependente \(\boldsymbol{y}\) mas ainda é necessário alguns ajustes finos no modelo.
Interpretação dos coeficientes
Ao vermos a fórmula de regressão de Poisson percebemos a interpretação dos coeficientes requer uma transformação. A transformação que precisamos fazer é a que inverte o logarítmo de \(\boldsymbol{y}\), no caso a função de exponenciação:
\[ \begin{aligned} \log(\boldsymbol{y}) &= \alpha + \mathbf{X} \boldsymbol{\beta} \\ \boldsymbol{y} &= e^{ \left( \alpha + \mathbf{X} \boldsymbol{\beta} \right) } \\ \boldsymbol{y} &= e^{\alpha} \cdot e^{\left( \mathbf{X} \boldsymbol{\beta} \right) } \end{aligned} \]
Fazemos isso com a função exp() do R nos coeficientes do model_poisson:
coeff <- exp(model_poisson$coefficients)
coeff
(Intercept) roach1 treatment senior
23.01 1.01 0.60 0.69 (Intercept): a taxa basal de exterminação das baratas \(\boldsymbol{y}\), \(23\)roach1: a cada uma barata antes da exterminação há um incremento de 1% de baratas exterminadastreatment: se o apartamento foi dedetizado há uma redução de 40% de baratas exterminadasenior: se o apartamento possui somente idosos há uma redução de 30% de barata exterminadas
Inflação de Zeros2 - Modelo Binomial Negativo
Às vezes temos dados de contagem na qual há uma super-inflação de zeros na variável dependente \(\boldsymbol{y}\). Nestes casos os modelos de Poisson podem não ser a melhor opção, pois ele força que a média e variância da variável dependente sejam iguais. Para isso é melhor usar função de verossimilhança binomial negativa. Lembrando que a distribuição negativa binomial tem dois parâmetros:
- Número de Sucessos (\(k\))
- Probabilidade de Sucessos (\(p\))
Qualquer fenômeno que pode ser modelo com uma distribuição de Poisson, pode ser modelo com uma distribuição binomial negativa (Gelman et al., 2013; Gelman, Hill, & Vehtari, 2020).
Usando a função de verossimilhança binomial negativa nosso modelo se torna:
\[ \begin{aligned} \boldsymbol{y} &\sim \text{Binomial Negativa} \left( e^{(\alpha + \mathbf{X} \boldsymbol{\beta})}, \phi \right) \\ \phi &\sim \text{Gamma}(0.01, 0.01) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \end{aligned} \]
Veja que, quando comparamos com o modelo de Poisson, temos uma novo parâmetro \(\phi\) que parametriza a distribuição binomial negativa. Esse parâmetro é a probabilidade de sucessos \(p\) da distribuição binomial negativa e geralmente usamos uma distribuição gamma como priori para que \(\phi\) cumpra a função de um parâmetro de “dispersão recíproca.”
Para usar funções de verossimilhança binomial negativa basta adicionar:
rstanarm:family = neg_binomial_2brms:family = negbinomial
Inflação de Zeros - Mistura Binomial Negativa
Mesmo usando uma função de verossimilhança binomial negativa, caso a superdispersão seja muito acentuada, o seu modelo ainda pode resultar em patologias. Uma outra sugestão é usar uma mistura com uma função de verossimilhança binomial negativa. Precisa de apenas uma única mudança na especificação do modelo:
\[ \boldsymbol{y} \begin{cases} = 0, &\text{ se } S_i = 0 \\ \sim \text{Binomial Negativa} \left( e^{(\alpha + \mathbf{X} \boldsymbol{\beta})}, \phi \right), &\text{ se } S_i = 1 \end{cases} \]
Aqui, \(S_i\) é uma variável binária (dummy) indicando se a observação \(i\) tem valor diferente de zero ou não. \(S_i\) pode ser modelado usando uma regressão logística:
\[ \begin{aligned} P(S_i = 1) &= \operatorname{logit}^{-1}(\mathbf{X} \boldsymbol{\gamma}) \\ \boldsymbol{\gamma} &\sim \text{Beta}(1, 1) \end{aligned} \]
onde \(\boldsymbol{\gamma}\) é um novo conjunto de coeficientes para essa parte do modelo com prioris uniformes de \(\text{Beta} (1, 1)\). Esse modelo de duas etapas (two-stage) pode ser feito apenas especificando family = zero_inflated_negbinomial no brms ou codificando diretamente no Stan. rstanarm não possui suporte para esse tipo de modelo baseado em uma mistura.
Exemplo Binomial Negativo - Revisitando a exterminação de baratas
Vamos dar uma olhada melhor no histograma da variável dependente y (figura 3). Como vocês podem ver, temos muitos zeros como observações de y:
ggplot(roaches, aes(y)) +
geom_histogram(bins = 15, fill = "steelblue") +
labs(
title = "Histograma da variável y",
y = "Frequência"
)
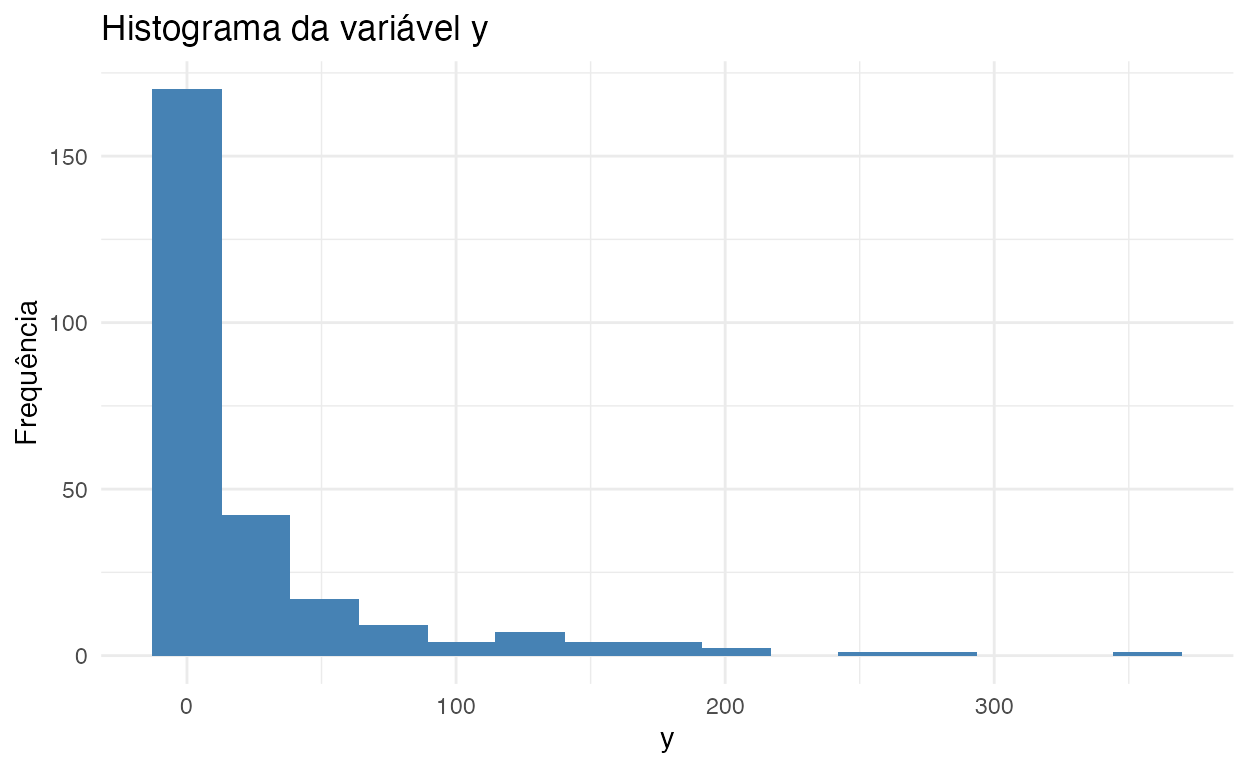
Figure 3: Histograma da variável y
roaches é um bom candidato para um modelo binomial negativo. Vamos então estimá-lo com o rstanarm. Aqui vou usar as mesmas prioris do modelo de Poisson. rstanarm por padrão usa a distribuição \(\text{Exponencial} (1)\) como priori de \(\phi\)3. Caso queira mudar é só especificar a sua priori desejada como argumento do prior_aux:
Vamos ver como ficaram as estimação dos parâmetros de interesse do modelo com summary():
summary(model_negbinomial)
Model Info:
function: stan_glm
family: neg_binomial_2 [log]
formula: y ~ roach1 + treatment + senior
algorithm: sampling
sample: 4000 (posterior sample size)
priors: see help('prior_summary')
observations: 262
predictors: 4
Estimates:
mean sd 10% 50% 90%
(Intercept) 2.8 0.2 2.6 2.8 3.1
roach1 0.0 0.0 0.0 0.0 0.0
treatment -0.7 0.2 -1.1 -0.7 -0.4
senior -0.3 0.3 -0.7 -0.3 0.0
reciprocal_dispersion 0.3 0.0 0.2 0.3 0.3
Fit Diagnostics:
mean sd 10% 50% 90%
mean_PPD 95.8 185.3 26.1 52.0 175.5
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.0 1.0 5328
roach1 0.0 1.0 5114
treatment 0.0 1.0 5261
senior 0.0 1.0 4957
reciprocal_dispersion 0.0 1.0 5319
mean_PPD 3.1 1.0 3636
log-posterior 0.0 1.0 1865
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).Não tivemos nenhum problema nas correntes Markov pois todos os Rhat estão bem abaixo de 1.01. Vejam que as inferências sobre os parâmetros estão diferentes do modelo de Poisson. Notem também que o número de amostras efetivas (Effective Sample Size - ESS) para todos os parâmetros do modelo negativo binomial estão bem mais elevadas que o modelo de Poisson, indicando que com a parametrização binomial negativa o amostrador MCMC de Stan conseguiu explorar muito melhor a posterior do que na parametrização de Poisson.
Vamos verificar o Posterior Predictive Check do modelo binomial negativo na figura 4:
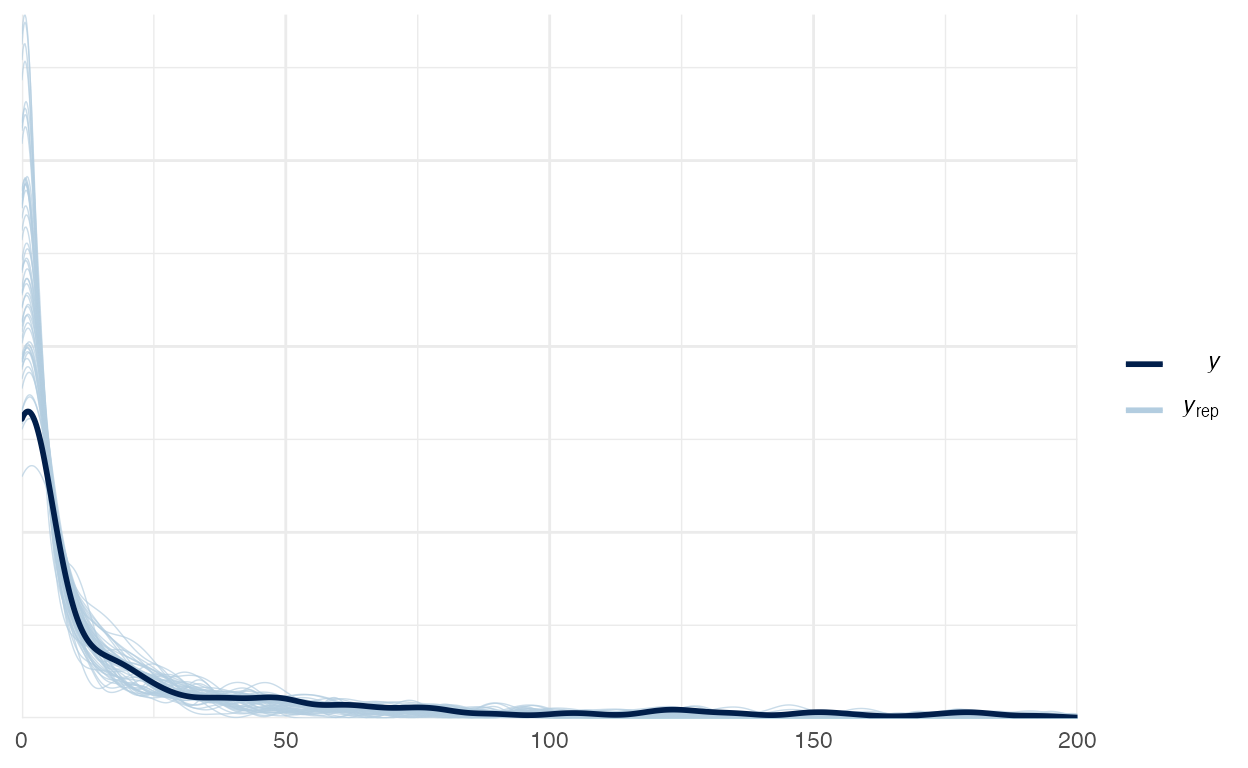
Figure 4: Posterior Preditive Check do modelo Binomial Negativo
Vemos também que Posterior Preditive Check do modelo binomial negativo possui um aspecto muito melhor que o modelo de Poisson.
Exemplo Mistura Binomial Negativo - \(\textbf{Revisitando}^2\) a exterminação de baratas
Vamos tentar aprimorar o modelo binomial negativo incorporando a mistura sugerida acima. Para isso teremos que usar o brms já que o rstanarm não possui suporte à misturas. Vou manter todas as prioris dos modelos anteriores. Mas para \(\phi\) usarei a distribuição \(\text{Gamma}(0.01, 0.01)\) (prior(gamma(0.01, 0.01), class = shape)) que possui suporte no brms e para os coeficientes \(\boldsymbol{\gamma}\) da segunda etapa do modelo usarei a priori uniforme \(\text{Beta}(1, 1)\) (prior(beta(1,1), class = zi)):
library(brms)
model_zero_inflated <- brm(
y ~ roach1 + treatment + senior,
data = roaches,
family = zero_inflated_negbinomial,
prior = c(
prior(normal(0, 0.1), class = b, coef = roach1),
prior(normal(0, 5), class = b, coef = treatment),
prior(normal(0, 5), class = b, coef = senior),
prior(normal(0, 2.5), class = Intercept),
prior(gamma(0.01, 0.01), class = shape),
prior(beta(1, 1), class = zi)
)
)
Vamos ver como ficaram as estimação dos parâmetros de interesse do modelo com summary():
summary(model_zero_inflated)
Family: zero_inflated_negbinomial
Links: mu = log; shape = identity; zi = identity
Formula: y ~ roach1 + treatment + senior
Data: roaches (Number of observations: 262)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 2.91 0.24 2.46 3.38 1.00 2888 2650
roach1 0.01 0.00 0.01 0.02 1.00 3467 2727
treatment -0.73 0.24 -1.20 -0.27 1.00 2895 2920
senior -0.31 0.27 -0.82 0.24 1.00 2396 2349
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
shape 0.30 0.04 0.23 0.40 1.00 1519 1115
zi 0.06 0.05 0.00 0.18 1.00 1261 1275
Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).Não tivemos nenhum problema nas correntes Markov pois todos os Rhat estão bem abaixo de 1.01. Vejam que as inferências sobre os parâmetros estão similares ao modelo negativo binomial, mas com menores erros (Est.Error no brms vs sd no rstanarm).
Vamos verificar o Posterior Predictive Check da mistura binomial negativa na figura 5:
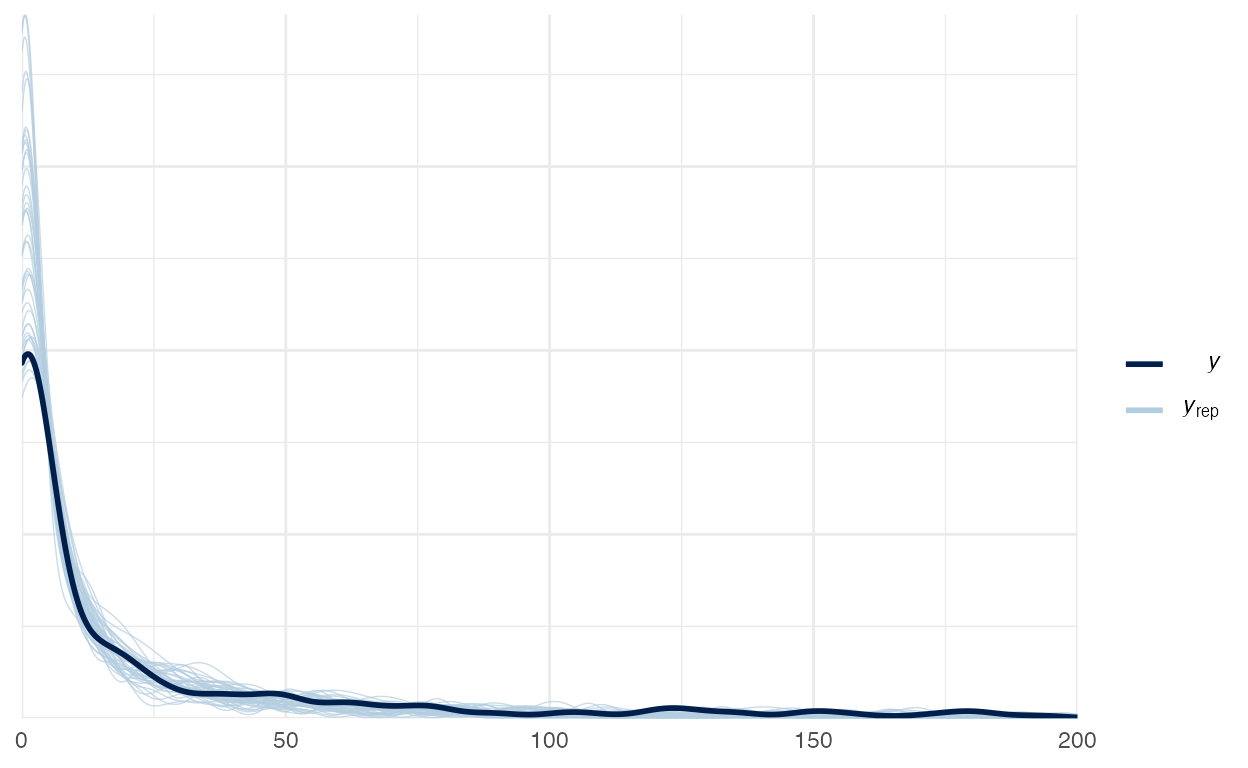
Figure 5: Posterior Preditive Check da mistura Binomial Negativa
As mistura negativa binomial tem quase o mesmo Posterior Preditive Check do modelo binomial, porém com menores erros de mensuração dos parâmetros de interesse. Isto nos satisfaz que das três alternativas aqui apresentadas a mistura negativa binomial é a melhor candidata para modelar roaches. O conteúdo auxiliar sobre Comparação de Modelos mostra como comparar modelos Bayesianos de maneira objetiva que é um aprimoramento sobre comparação subjetivas de gráficos de Posterior Predictive Check.
Atividade Prática
Veja o dataset NYC_bicycle que está disponível no diretório datasets/:
- New York City - East River Bicycle Crossings:
datasets/NYC_bicycle.csv
###
Ambiente
R version 4.1.0 (2021-05-18)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Big Sur 11.4
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] brms_2.15.0 skimr_2.1.3 rstanarm_2.21.1 Rcpp_1.0.6
[5] tibble_3.1.2 ggplot2_3.3.3
loaded via a namespace (and not attached):
[1] minqa_1.2.4 colorspace_2.0-1 ellipsis_0.3.2
[4] ggridges_0.5.3 rsconnect_0.8.18 estimability_1.3
[7] markdown_1.1 base64enc_0.1-3 farver_2.1.0
[10] rstan_2.21.2 DT_0.18 fansi_0.5.0
[13] mvtnorm_1.1-2 bridgesampling_1.1-2 codetools_0.2-18
[16] splines_4.1.0 downlit_0.2.1 knitr_1.33
[19] shinythemes_1.2.0 bayesplot_1.8.0 projpred_2.0.2
[22] jsonlite_1.7.2 nloptr_1.2.2.2 shiny_1.6.0
[25] compiler_4.1.0 emmeans_1.6.1 backports_1.2.1
[28] assertthat_0.2.1 Matrix_1.3-3 fastmap_1.1.0
[31] cli_2.5.0 later_1.2.0 htmltools_0.5.1.1
[34] prettyunits_1.1.1 tools_4.1.0 igraph_1.2.6
[37] coda_0.19-4 gtable_0.3.0 glue_1.4.2
[40] reshape2_1.4.4 dplyr_1.0.6 V8_3.4.2
[43] jquerylib_0.1.4 vctrs_0.3.8 nlme_3.1-152
[46] crosstalk_1.1.1 xfun_0.23 stringr_1.4.0
[49] ps_1.6.0 lme4_1.1-27 mime_0.10
[52] miniUI_0.1.1.1 lifecycle_1.0.0 gtools_3.9.2
[55] MASS_7.3-54 zoo_1.8-9 scales_1.1.1
[58] colourpicker_1.1.0 ragg_1.1.3 promises_1.2.0.1
[61] Brobdingnag_1.2-6 parallel_4.1.0 inline_0.3.19
[64] shinystan_2.5.0 gamm4_0.2-6 yaml_2.2.1
[67] curl_4.3.1 gridExtra_2.3 loo_2.4.1
[70] StanHeaders_2.21.0-7 sass_0.4.0 distill_1.2
[73] stringi_1.6.2 highr_0.9 dygraphs_1.1.1.6
[76] boot_1.3-28 pkgbuild_1.2.0 repr_1.1.3
[79] rlang_0.4.11 pkgconfig_2.0.3 systemfonts_1.0.2
[82] matrixStats_0.59.0 evaluate_0.14 lattice_0.20-44
[85] purrr_0.3.4 rstantools_2.1.1 htmlwidgets_1.5.3
[88] labeling_0.4.2 processx_3.5.2 tidyselect_1.1.1
[91] plyr_1.8.6 magrittr_2.0.1 R6_2.5.0
[94] generics_0.1.0 DBI_1.1.1 mgcv_1.8-35
[97] pillar_1.6.1 withr_2.4.2 xts_0.12.1
[100] survival_3.2-11 abind_1.4-5 crayon_1.4.1
[103] utf8_1.2.1 rmarkdown_2.8 grid_4.1.0
[106] callr_3.7.0 threejs_0.3.3 digest_0.6.27
[109] xtable_1.8-4 tidyr_1.1.3 httpuv_1.6.1
[112] textshaping_0.3.5 RcppParallel_5.1.4 stats4_4.1.0
[115] munsell_0.5.0 bslib_0.2.5.1 shinyjs_2.0.0