Todos os testes aqui descritos possuem uma única finalidade: identificar se a média de variável entre dois grupos é diferente. Todos possuem como hipótese nula a diferença entre os grupos é zero, então \(p\)-valores oriundos dos testes quantificam a probabilidade de você obter resultados tão extremos caso não haja diferença entre os grupos. Por fim, todos os testes possuem o pressuposto de independência dos dados, portanto, caso haja alguma fonte de dependência dos dados os resultados dos testes são inválidos.
Teste \(t\) de Student
William Sealy Gosset (químico, 1876-1937) publicou o teste \(t\) sob o pseudônimo de “Student,” razão pela qual o teste às vezes é chamado de “teste \(t\) de Student” (Student, 1908). Há controvérsia sobre a origem e o significado de \(t\). Uma hipótese é que \(s\) era comumente usado na época para se referir a estatísticas de amostra, então Gosset escolheu \(t\) como a próxima letra, talvez indicando um “avanço” no pensamento sobre estatísticas de amostra. Gosset publicou sob um pseudônimo porque ele era um funcionário da Cervejaria Guinness na época, e ele foi contratado para examinar questões ao fazer inferências sobre pequenas amostras na fabricação de cerveja. O teste que ele desenvolveu poderia ser propriedade intelectual do Guinness, mas Gosset achou que o teste poderia ser amplamente usado, então ele o publicou sob um pseudônimo para proteger seu trabalho.

Figure 1: William Sealy Gosset. Figura de https://www.wikipedia.org
O teste \(t\) de Student assume os seguintes pressupostos com relação aos dados:
- Os dados são independentes: o valor de uma observação não influencia ou afeta o valor de outras observações.
- A variável dependente (aquela que estamos usando para calcular a média dos grupos) é distribuída conforme uma distribuição Normal.
- A variável dependente possui homogeneidade de variância dentre os grupos1.
Student vs Welch
Em 1947, Bernard Lewis Welch, estatístico britânico adaptou o teste \(t\) de Student para ser robusto perante heterogeneidade das variâncias (Welch, 1947). O teste \(t\) de Welch é muita vezes confudido e reportado erroneamente como teste \(t\) de Student, uma vez que pela sua robustez é o teste \(t\) padrão de diversos softwares estatísticos (Delacre, Lakens, & Leys, 2017). No R a função t.test() possui como padrão o teste \(t\) de Welch e caso você queira explicitamente usar o teste \(t\) de Student você deve incluir o argumento var.equal = TRUE na função.
Teste \(t\) para Amostras Independentes
Quando temos dois grupos na mesma amostra, usamos o teste \(t\) para amostras independentes. A função t.test() é incluída como padrão no R. Aqui vamos simular dois grupos A e B cada um com 20 observações e vamos amostrar de uma distribuição Normal para cada um dos grupos com médias diferentes.
A fórmula que deve ser passada na função t.test() segue a mesma lógica das fórmulas do Teste de Bartlett e de Levene, sendo que é necessário fornecer dois argumentos:
- Fórmula designando a variável cuja média deve ser analisada e os grupos em relação aos quais as médias serão analisadas. A fórmula é designada pela seguinte síntaxe:
variavel ~ grupo. - O dataset no qual deverá ser encontrados tanto a varíavel quanto os grupos.
O resultado para a simulação é um \(p\)-valor menor que 0.05, ou seja um resultado significante apontando que podemos rejeitar a hipótese nula (fortes evidências contrárias que as médias dos grupos são iguais).
library(ggplot2)
library(dplyr)
n_sim_t <- 20
sim3 <- tibble(
group = c(rep("A", n_sim_t), rep("B", n_sim_t)),
measure = c(rnorm(n_sim_t, mean = 0), rnorm(n_sim_t, mean = 5))
)
t.test(measure ~ group, data = sim3)
Welch Two Sample t-test
data: measure by group
t = -13.095, df = 37.88, p-value = 1.226e-15
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-5.086532 -3.724278
sample estimates:
mean in group A mean in group B
0.2039198 4.6093247 Teste \(t\) para duas Amostras Pareadas
Em algumas situações temos amostras pareadas, como por exemplo quando fazemos uma mensuração antes e depois de algum acontecimento ou intervenção. Para isso a função t.test() tem o argumento paired que quando definido como TRUE faz com que o teste \(t\) seja pareado.
A mesma simulação do teste \(t\) para amostras pareadas, mas agora não usamos a fórmula e passamos como argumento as mensurações das duas amostras pareadas:
amostra_1 <- tibble(measure = rnorm(n_sim_t, mean = 0))
amostra_2 <- tibble(measure = rnorm(n_sim_t, mean = 5))
t.test(amostra_1$measure, amostra_2$measure, paired = TRUE)
Paired t-test
data: amostra_1$measure and amostra_2$measure
t = -14.839, df = 19, p-value = 6.656e-12
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-5.810596 -4.374036
sample estimates:
mean of the differences
-5.092316 Testes \(t\) Não-Paramétricos
O que fazer se meus dados violam o pressuposto de normalidade? Nesse caso devemos usar uma abordagem não-paramétrica. O teste \(t\) de Student (e também de Welch) é uma abordagem paramétrica: dependem fortemente da suposição que os dados estejam distribuídos de acordo com uma distribuição específica. Testes não-paramétricos não fazem suposições sobre a distribuição dos dados e portanto podem ser usados quando os pressupostos dos testes paramétricos são violados.
Atenção: testes não-paramétricos são menos sensíveis em rejeitar a hipótese nula quando ela é verdadeira (erro tipo I) do que testes paramétricos quando o pressuposto de normalidade não é violado (Zimmerman, 1998). Então não pense que deve sempre aplicar um teste não-paramétrico em todas as ocasiões.
Teste de Mann–Whitney
O teste de Mann-Whitney foi desenvolvido em 1947 para ser uma alternativa não-paramétrica ao teste \(t\) para amostras independentes (Mann & Whitney, 1947). Para aplicar o teste Mann-Whitney use a função wilcox.test()2 é incluída como padrão no R. Aqui vamos simular novemente dois grupos A e B cada um com 20 observações e vamos amostrar de uma distribuição Log-Normal para cada um dos grupos com médias diferentes. A síntaxe é a mesma que a função t.test().
sim4 <- tibble(
group = c(rep("A", n_sim_t), rep("B", n_sim_t)),
measure = c(rlnorm(n_sim_t, mean = 0), rlnorm(n_sim_t, mean = 5))
)
wilcox.test(measure ~ group, data = sim4, conf.int = TRUE)
Wilcoxon rank sum exact test
data: measure by group
W = 0, p-value = 1.451e-11
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-197.1586 -106.6526
sample estimates:
difference in location
-127.4953 Teste de Wilcoxon
O teste de Wilcoxon foi desenvolvido em 1945 para ser uma alternativa não-paramétrica ao teste \(t\) para amostras pareadas (Wilcoxon, 1945). A função wilcox.test()3 tem o argumento paired que quando definido como TRUE faz com que o teste não-paramétrico seja pareado (muito similar a função t.test() para amostras pareadas).
A mesma simulação do teste de Mann-Whitney para amostras pareadas, mas agora não usamos a fórmula e passamos como argumento as mensurações das duas amostras pareadas:
amostra_3 <- tibble(measure = rlnorm(n_sim_t, mean = 0))
amostra_4 <- tibble(measure = rlnorm(n_sim_t, mean = 5))
wilcox.test(amostra_3$measure, amostra_4$measure, paired = TRUE, conf.int = TRUE)
Wilcoxon signed rank exact test
data: amostra_3$measure and amostra_4$measure
V = 0, p-value = 1.907e-06
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-214.98044 -98.24208
sample estimates:
(pseudo)median
-144.3723 Como visualizar testes de média entre grupos com R
Uma das bibliotecas que usamos bastante para visualização de testes estatísticos é a {ggpubr} (Kassambara, 2020). Veja um exemplo abaixo com um dos datasets que simulamos nesse tutorial.
Primeiramente criamos um diagrama de caixa (boxplot) com a função ggboxplot() na qual especificamos o eixo X, eixo Y, cor, paleta de cores etc. Na sequencia adicionamos a camada das estatísticas de comparação dos grupos com o stat_compare_means() especificando que tipo de método será utilizado na análise:
"wilcox.test"– Teste não-paramétrico de Wilcoxon (padrão da função)."t.test"– Teste \(t\) paramétrico de Welch.
library(ggpubr)
ggboxplot(sim3, x = "group", y = "measure", color = "group",
palette = "lancet", add = "jitter") +
stat_compare_means(method = "t.test")
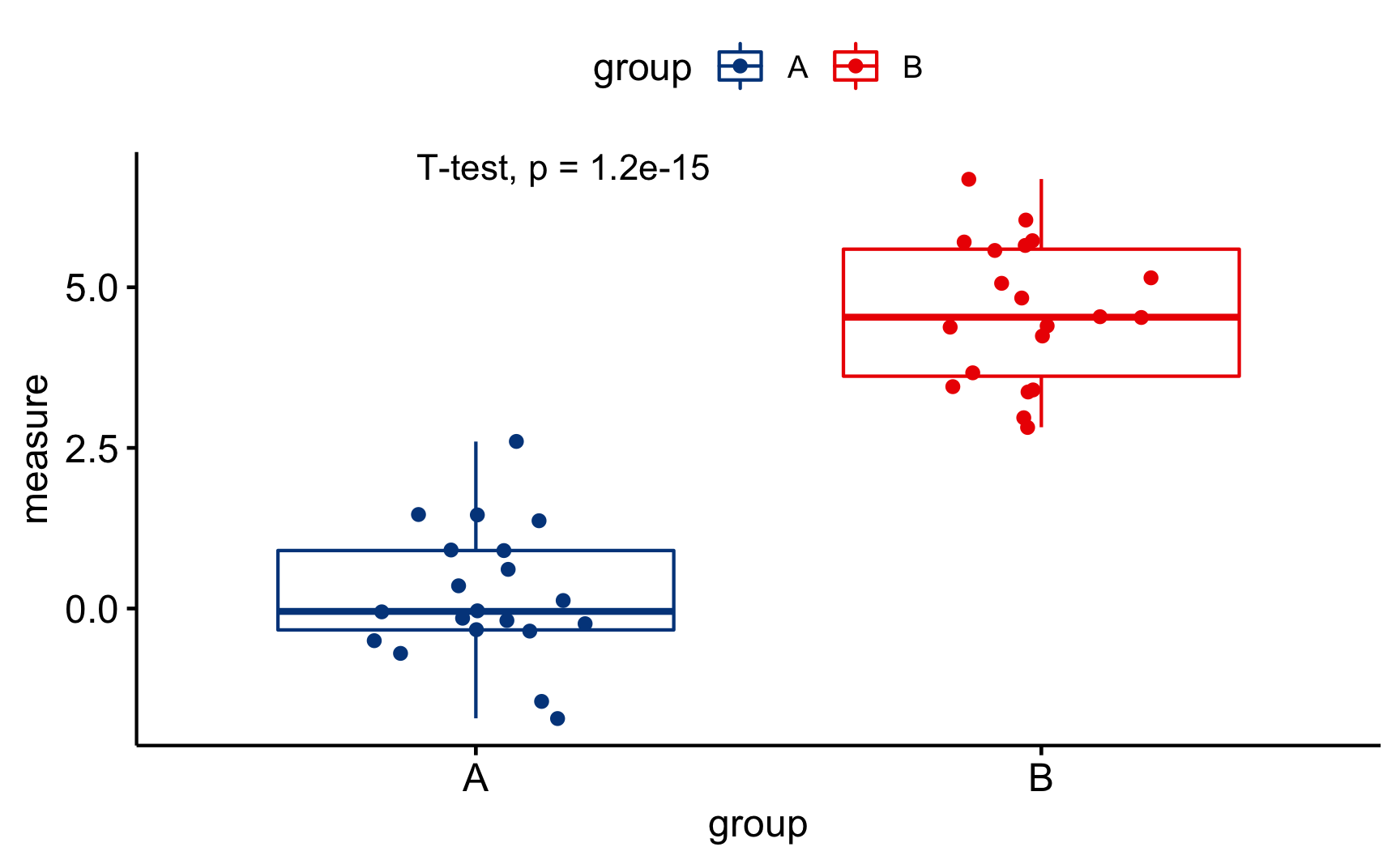
Figure 2: Diagrama de Caixa usando o {ggpubr} – Amostras Independentes
Para testes usando amostras pareadas é necessário usar a função ggpaired() e adicionar o argumento paired = TRUE dentro da função stat_compare_means()
ggpaired(sim3, x = "group", y = "measure", color = "group",
palette = "lancet", line.color = "gray", line.size = 0.4) +
stat_compare_means(method = "t.test", paired = TRUE)
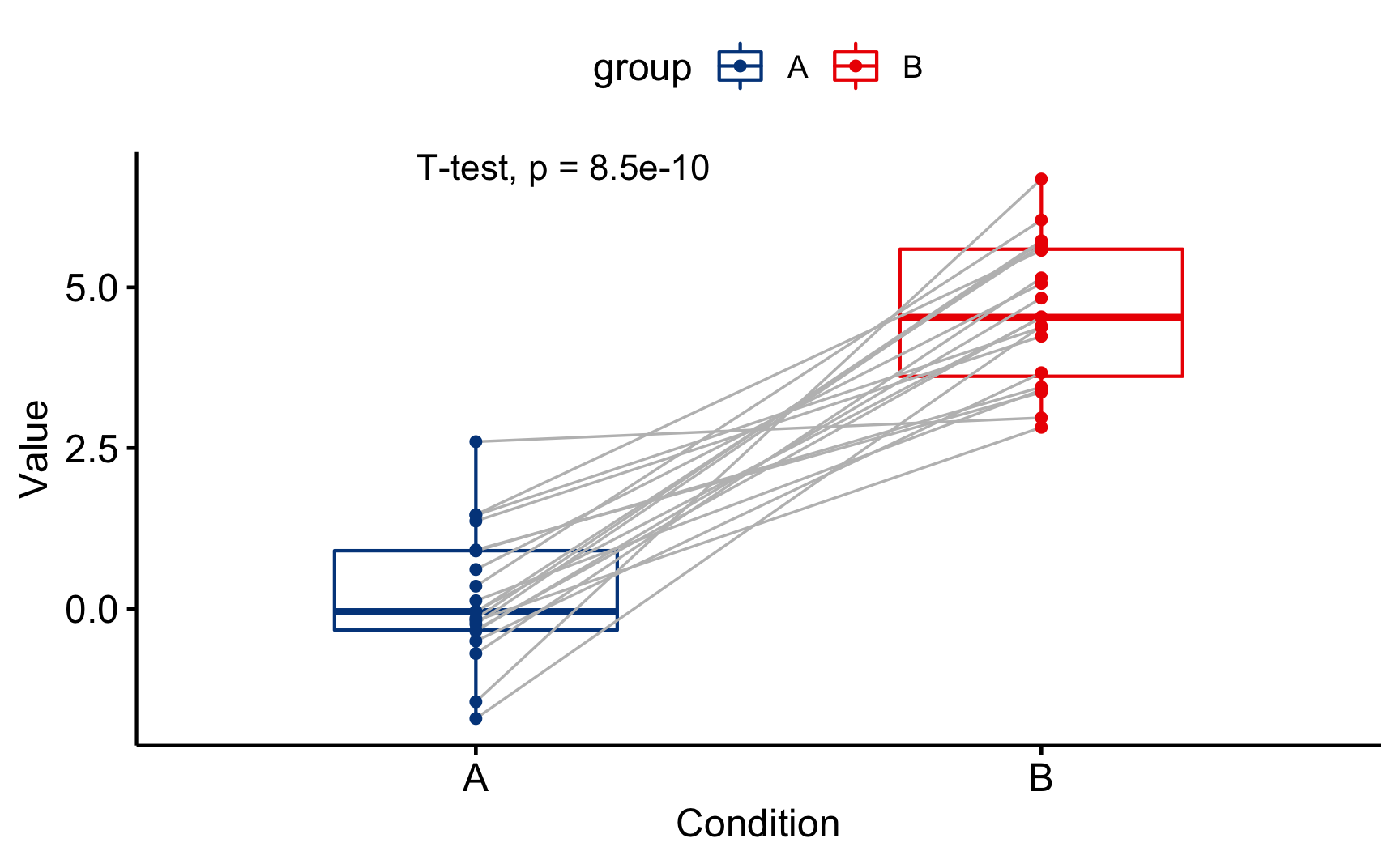
Figure 3: Diagrama de Caixa usando o {ggpubr} – Amostras Pareadas
Ambiente
R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] ggpubr_0.4.0 car_3.0-10 carData_3.0-4
[4] patchwork_1.1.1 dplyr_1.0.4 ggplot2_3.3.3
[7] DiagrammeR_1.0.6.1 readxl_1.3.1
loaded via a namespace (and not attached):
[1] Rcpp_1.0.6 lubridate_1.7.9.2 lattice_0.20-41
[4] tidyr_1.1.2 visNetwork_2.0.9 assertthat_0.2.1
[7] rprojroot_2.0.2 digest_0.6.27 utf8_1.1.4
[10] R6_2.5.0 cellranger_1.1.0 backports_1.2.1
[13] evaluate_0.14 highr_0.8 pillar_1.4.7
[16] rlang_0.4.10 curl_4.3 rstudioapi_0.13
[19] data.table_1.13.6 Matrix_1.2-18 reticulate_1.18
[22] rmarkdown_2.6 labeling_0.4.2 stringr_1.4.0
[25] foreign_0.8-80 htmlwidgets_1.5.3 munsell_0.5.0
[28] broom_0.7.4 compiler_4.0.3 xfun_0.21
[31] pkgconfig_2.0.3 htmltools_0.5.1.1 downlit_0.2.1
[34] tidyselect_1.1.0 tibble_3.0.6 bookdown_0.21
[37] rio_0.5.16 fansi_0.4.2 crayon_1.4.1
[40] withr_2.4.1 grid_4.0.3 jsonlite_1.7.2
[43] gtable_0.3.0 lifecycle_0.2.0 DBI_1.1.1
[46] magrittr_2.0.1 scales_1.1.1 zip_2.1.1
[49] cli_2.3.0 stringi_1.5.3 ggsignif_0.6.0
[52] farver_2.0.3 xml2_1.3.2 ellipsis_0.3.1
[55] generics_0.1.0 vctrs_0.3.6 openxlsx_4.2.3
[58] distill_1.2 ggsci_2.9 RColorBrewer_1.1-2
[61] tools_4.0.3 forcats_0.5.1 glue_1.4.2
[64] purrr_0.3.4 hms_1.0.0 abind_1.4-5
[67] yaml_2.2.1 colorspace_2.0-0 rstatix_0.6.0
[70] knitr_1.31 haven_2.3.1 Uma versão do teste \(t\) de Welch é robusta a heterogeneidade de variâncias e permite com que esse pressuposto seja violado.↩︎
O teste Mann-Whitney também e chamado de teste de Mann–Whitney–Wilcoxon (MWW), teste da soma dos postos de Wilcoxon e teste de Wilcoxon–Mann–Whitney. Por isso o nome da função R para teste de Mann-Whitney é
wilcox.test().↩︎Teste de Wilcoxon também e conhecido como testes dos postos sinalizados de Wilcoxon.↩︎