O quarteto de Anscombe compreende quatro conjuntos de dados que têm estatísticas descritivas simples quase idênticas, mas têm distribuições muito diferentes e parecem muito diferentes quando representados graficamente. Cada conjunto de dados consiste em onze (x, y) pontos. Eles foram construídos em 1973 pelo estatístico Francis Anscombe (Anscombe, 1973) para demonstrar a importância dos dados gráficos antes de analisá-los e o efeito de outliers e outras observações influentes nas propriedades estatísticas. Ele descreveu o artigo como tendo a intenção de contrariar a impressão entre os estatísticos de que “os cálculos numéricos são exatos, mas os gráficos são aproximados.”
Falamos na tutorial 2 de \(p\)-valores que “somos adeptos de visualizações e usamos constantemente nas nossas análises. Mas, na Estatística, as visualizações são muito boas para mostrar alguma tendência, característica ou peculiaridade dos dados. Agora, para provar algo, é necessário um teste estatístico.” Para mostrar a importância dos gráficos vamos explorar um pouco os 4 conjuntos de dados do quarteto de Anscombe. A moral da história aqui é que se deve olhar um conjunto de dados graficamente antes de começar a analisar de acordo com um tipo particular de relacionamento, além da inadequação das propriedades estatísticas básicas para descrever conjuntos de dados realistas.
Dataset anscombe
O R possui como padrão o dataset anscombe que pode ser carregado pela função data() sem a instalação de qualquer biblioteca adicional. O dataset anscombe possui os quatro conjuntos de (x,y) como colunas (variáveis) e são identificadas de x1 e y1 à x4 e y4. Veja na tabela abaixo as onze observações dos quatro conjuntos de Anscombe do dataset anscombe1:
library(gt)
data("anscombe")
gt(anscombe, rownames_to_stub = TRUE) %>%
tab_header(title = "Quarteto de Anscombe")
| Quarteto de Anscombe | ||||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | y1 | y2 | y3 | y4 | |
| 1 | 10 | 10 | 10 | 8 | 8.04 | 9.14 | 7.46 | 6.58 |
| 2 | 8 | 8 | 8 | 8 | 6.95 | 8.14 | 6.77 | 5.76 |
| 3 | 13 | 13 | 13 | 8 | 7.58 | 8.74 | 12.74 | 7.71 |
| 4 | 9 | 9 | 9 | 8 | 8.81 | 8.77 | 7.11 | 8.84 |
| 5 | 11 | 11 | 11 | 8 | 8.33 | 9.26 | 7.81 | 8.47 |
| 6 | 14 | 14 | 14 | 8 | 9.96 | 8.10 | 8.84 | 7.04 |
| 7 | 6 | 6 | 6 | 8 | 7.24 | 6.13 | 6.08 | 5.25 |
| 8 | 4 | 4 | 4 | 19 | 4.26 | 3.10 | 5.39 | 12.50 |
| 9 | 12 | 12 | 12 | 8 | 10.84 | 9.13 | 8.15 | 5.56 |
| 10 | 7 | 7 | 7 | 8 | 4.82 | 7.26 | 6.42 | 7.91 |
| 11 | 5 | 5 | 5 | 8 | 5.68 | 4.74 | 5.73 | 6.89 |
Visualizações
Aqui na figura 1 vocês podem observar a diferença entre os quatro conjuntos de Anscombe:
- O primeiro gráfico de dispersão (canto superior esquerdo) parece ser uma relação linear simples, correspondendo a duas variáveis correlacionadas onde
ypode ser modelado como gaussiano com a média linearmente dependente dex. - O segundo gráfico (canto superior direito) não é distribuído Normalmente; embora uma relação entre as duas variáveis seja óbvia, não é linear e o coeficiente de correlação de Pearson não é relevante. Uma regressão usando um termo quadrático (\(x^2\)) seria mais apropriada.
- No terceiro gráfico (canto inferior esquerdo), a distribuição é linear, mas deve ter uma linha de regressão diferente (uma regressão robusta teria sido necessária). A regressão calculada é compensada por um outlier que exerce influência suficiente para diminuir o coeficiente de correlação de 1 para 0.816.
- Finalmente, o quarto gráfico (canto inferior direito) mostra um exemplo em que um ponto de alta influência é suficiente para produzir um alto coeficiente de correlação, embora os outros pontos de dados não indiquem qualquer relação entre as variáveis.
library(ggplot2)
anscombe %>%
ggplot(aes(x, y, group = conjunto)) +
geom_point() +
geom_smooth(method = "lm", color = "Red", se = FALSE) +
facet_wrap(~ conjunto, labeller = "label_both", ncol = 2) +
theme(legend.position = "none")
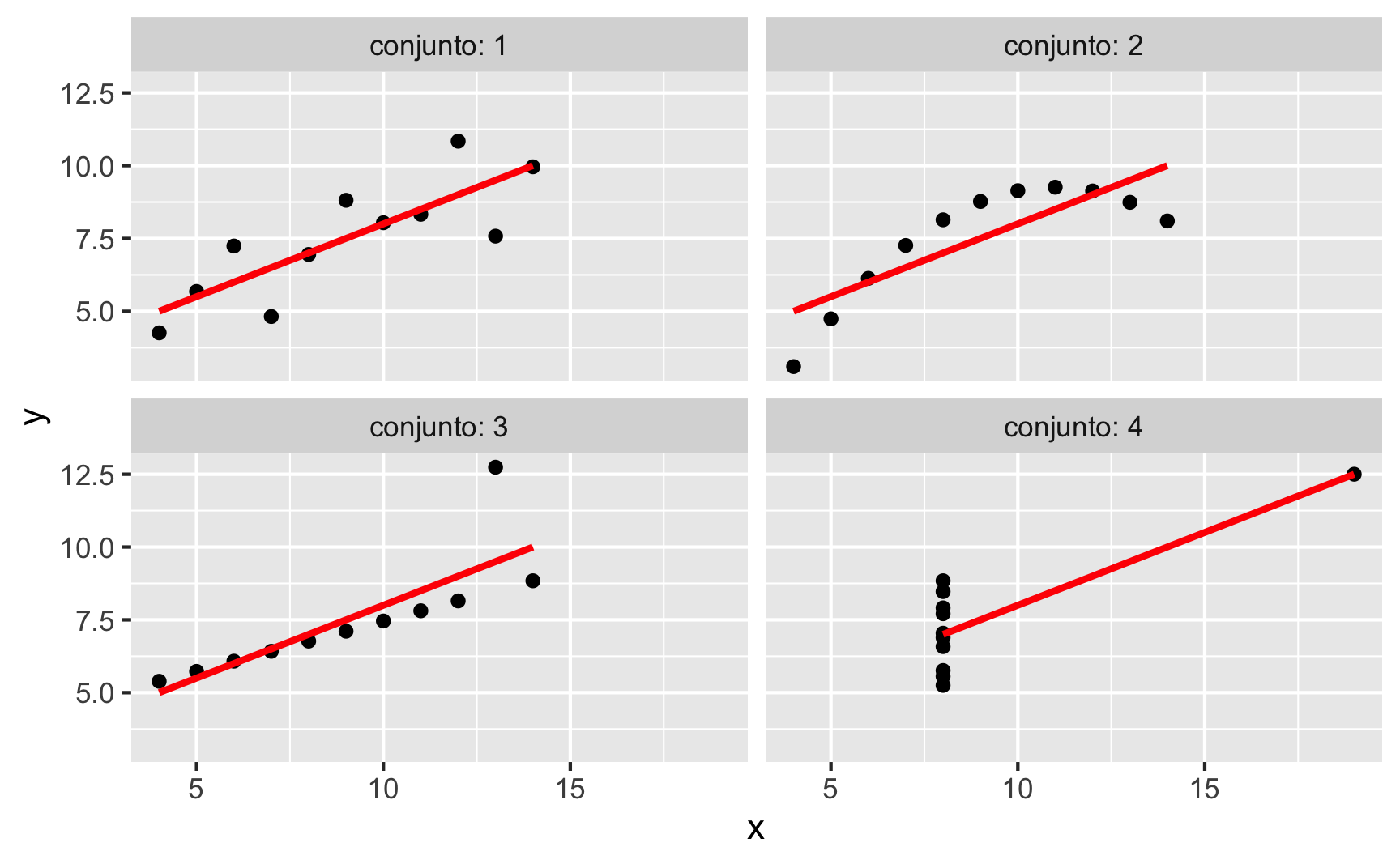
Figure 1: O quarteto de Anscombe
Estatísticas Descritivas
O mais intrigante é que esses quatro conjuntos, quando visualizados demonstram sem dúvida quatro naturezas de relações entre variáveis diferentes; mas quando analisamos apenas as estatísticas descritivas temos o mesmo resultado, conforme demonstrado na tabela com estatísticas descritivas dos quatro conjuntos2:
library(gtsummary)
theme_gtsummary_language("pt")
tbl_summary(anscombe,
by = conjunto,
type = all_continuous() ~ "continuous2",
statistic = list(
all_continuous() ~ c("{mean}",
"{sd}")),
digits = all_continuous() ~ 2) %>%
bold_labels() %>%
italicize_levels() %>%
as_gt() %>%
tab_header(title = "Estatísticas Descritivas do Quarteto de Anscombe",
subtitle = "Agrupadas por Conjunto")
| Estatísticas Descritivas do Quarteto de Anscombe | ||||
|---|---|---|---|---|
| Agrupadas por Conjunto | ||||
| Características | 1, N = 11 | 2, N = 11 | 3, N = 11 | 4, N = 11 |
| x | ||||
| Média | 9.00 | 9.00 | 9.00 | 9.00 |
| Desvio Padrão | 3.32 | 3.32 | 3.32 | 3.32 |
| y | ||||
| Média | 7.50 | 7.50 | 7.50 | 7.50 |
| Desvio Padrão | 2.03 | 2.03 | 2.03 | 2.03 |
Além disso, a correlação é a mesma (0.8163662) nos quatro conjuntos:
library(dplyr)
library(purrr)
tibble(conjunto = as.factor(1:4),
correlação = unique(anscombe$conjunto) %>%
map_dbl(~ cor(subset(anscombe, conjunto == .x, select = x),
subset(anscombe, conjunto == .x, select = y)))) %>%
gt() %>%
tab_header(title = "Correlações do Quarteto de Anscombe") %>%
tab_source_note(md("*Observação: Correlação calculada conforme a correlação de Pearson*"))
| Correlações do Quarteto de Anscombe | |
|---|---|
| conjunto | correlação |
| 1 | 0.8164205 |
| 2 | 0.8162365 |
| 3 | 0.8162867 |
| 4 | 0.8165214 |
| Observação: Correlação calculada conforme a correlação de Pearson | |
Modelos de Regressão
O mais interessante é que se formos aplicar uma regressão linear teremos os mesmo \(p\)-valores, coeficientes, \(R^2\) e \(R^2\) ajustado para todos os quatro conjuntos. Veja na tabela abaixo:
library(broom)
map_dfr(1:4,
~ tidy(lm(y ~ x, subset(anscombe, conjunto == .x)), conf.int = TRUE)) %>%
filter(term == "x") %>%
mutate(Conjunto = unique(anscombe$conjunto)) %>%
inner_join(map_dfr(unique(anscombe$conjunto),
~ glance(lm(y ~ x, subset(anscombe, conjunto == .x)),
conf.int = TRUE)) %>%
mutate(Conjunto = unique(anscombe$conjunto)),
by = "Conjunto") %>%
relocate(Conjunto) %>%
dplyr::select(Conjunto, estimate, std.error, p.value.x,
conf.low, conf.high, r.squared, adj.r.squared) %>%
gt() %>%
tab_header("Modelo de Regressão Linear do Quarteto de Anscombe",
md("Fórmula: `y ~ x`"))
| Modelo de Regressão Linear do Quarteto de Anscombe | |||||||
|---|---|---|---|---|---|---|---|
Fórmula: y ~ x |
|||||||
| Conjunto | estimate | std.error | p.value.x | conf.low | conf.high | r.squared | adj.r.squared |
| 1 | 0.5000909 | 0.1179055 | 0.002169629 | 0.2333701 | 0.7668117 | 0.6665425 | 0.6294916 |
| 2 | 0.5000000 | 0.1179637 | 0.002178816 | 0.2331475 | 0.7668525 | 0.6662420 | 0.6291578 |
| 3 | 0.4997273 | 0.1178777 | 0.002176305 | 0.2330695 | 0.7663851 | 0.6663240 | 0.6292489 |
| 4 | 0.4999091 | 0.1178189 | 0.002164602 | 0.2333841 | 0.7664341 | 0.6667073 | 0.6296747 |
Uma maneira de diferenciar os quatro conjuntos de Anscombe numa regressão linear é analisar os seus resíduos, conforme figura 2. Aqui claramente vemos que apenas o gráfico do canto superior direito possui resíduos nos quais não é possível identificar nenhum padrão ou característica3.
library(patchwork)
map(1:4, ~ lm(y ~ x, subset(anscombe, conjunto == .x))) %>%
map2(1:4,
~ ggplot(augment(.x), aes(x = .fitted, y = .resid)) +
geom_point() +
geom_smooth(se = FALSE, method = "lm") +
labs(
x = "Valor de x",
y = "Resíduos",
title = paste("Conjunto", as.character(.y))
)) %>%
reduce(`+`) +
plot_layout(ncol = 2)
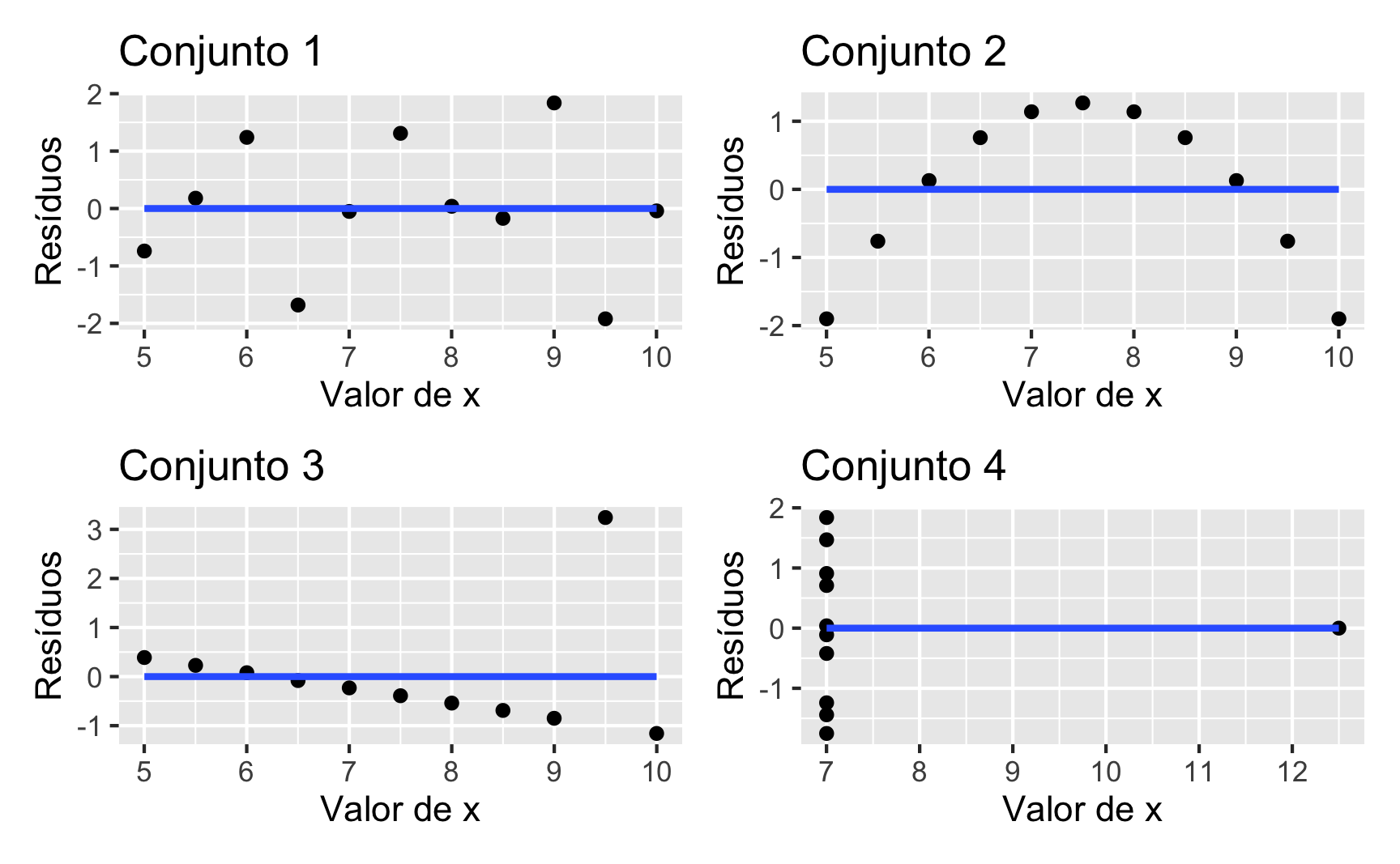
Figure 2: Resíduos dos Modelos de Regressão Linear Quarteto de Anscombe
Inclusive quando fazemos o teste studentizado de Breusch-Pagan(Breusch & Pagan, 1979; Koenker, 1981), todos os modelos falham em rejeitar a hipótese nula de que “a variância dos resíduos são iguais.” Provavelmente isto se deve por conta do tamanho da amostra ser pequeno (\(n=11\)) em todos os quatro conjuntos.
studentized Breusch-Pagan test
data: lm(y ~ x, subset(anscombe, conjunto == 1))
BP = 0.65531, df = 1, p-value = 0.4182
studentized Breusch-Pagan test
data: lm(y ~ x, subset(anscombe, conjunto == 2))
BP = 8.0774e-31, df = 1, p-value = 1
studentized Breusch-Pagan test
data: lm(y ~ x, subset(anscombe, conjunto == 3))
BP = 2.7234, df = 1, p-value = 0.09889
studentized Breusch-Pagan test
data: lm(y ~ x, subset(anscombe, conjunto == 4))
BP = 1.1821, df = 1, p-value = 0.2769Comentários Finais
O quarteto de Anscombe (Anscombe, 1973) é uma maneira de ilustrar a importância de visualizações na análise de dados. Deve-se sempre olhar um conjunto de dados graficamente antes de começar a qualquer análise. Em especial, são ilustrados diversos contextos nos quais as propriedades estatísticas básicas para descrever conjuntos de dados são inadequadas.
Ambiente
R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] purrr_0.3.4 gtsummary_1.3.6 gt_0.2.2
[4] lm.beta_1.5-1 lmtest_0.9-38 zoo_1.8-8
[7] ggfortify_0.4.11 sjPlot_2.8.7 broom_0.7.4
[10] palmerpenguins_0.1.0 magrittr_2.0.1 mnormt_2.0.2
[13] cowplot_1.1.1 tidyr_1.1.2 DescTools_0.99.40
[16] skimr_2.1.2 ggpubr_0.4.0 car_3.0-10
[19] carData_3.0-4 patchwork_1.1.1 dplyr_1.0.4
[22] ggplot2_3.3.3 DiagrammeR_1.0.6.1 readxl_1.3.1
loaded via a namespace (and not attached):
[1] backports_1.2.1 repr_1.1.3 splines_4.0.3
[4] usethis_2.0.1 digest_0.6.27 htmltools_0.5.1.1
[7] magick_2.6.0 fansi_0.4.2 checkmate_2.0.0
[10] openxlsx_4.2.3 modelr_0.1.8 colorspace_2.0-0
[13] haven_2.3.1 xfun_0.21 crayon_1.4.1
[16] jsonlite_1.7.2 Exact_2.1 lme4_1.1-26
[19] survival_3.2-7 glue_1.4.2 gtable_0.3.0
[22] emmeans_1.5.4 sjstats_0.18.1 sjmisc_2.8.6
[25] abind_1.4-5 scales_1.1.1 mvtnorm_1.1-1
[28] DBI_1.1.1 rstatix_0.6.0 ggeffects_1.0.1
[31] Rcpp_1.0.6 xtable_1.8-4 performance_0.7.0
[34] tmvnsim_1.0-2 reticulate_1.18 foreign_0.8-80
[37] htmlwidgets_1.5.3 RColorBrewer_1.1-2 ellipsis_0.3.1
[40] pkgconfig_2.0.3 farver_2.0.3 sass_0.3.1
[43] utf8_1.1.4 tidyselect_1.1.0 labeling_0.4.2
[46] rlang_0.4.10 effectsize_0.4.3 munsell_0.5.0
[49] cellranger_1.1.0 tools_4.0.3 visNetwork_2.0.9
[52] cli_2.3.0 generics_0.1.0 sjlabelled_1.1.7
[55] evaluate_0.14 stringr_1.4.0 yaml_2.2.1
[58] fs_1.5.0 knitr_1.31 zip_2.1.1
[61] rootSolve_1.8.2.1 nlme_3.1-149 xml2_1.3.2
[64] compiler_4.0.3 rstudioapi_0.13 curl_4.3
[67] e1071_1.7-4 ggsignif_0.6.0 tibble_3.0.6
[70] statmod_1.4.35 broom.helpers_1.1.0 stringi_1.5.3
[73] highr_0.8 parameters_0.11.0 forcats_0.5.1
[76] lattice_0.20-41 Matrix_1.2-18 commonmark_1.7
[79] nloptr_1.2.2.2 ggsci_2.9 vctrs_0.3.6
[82] pillar_1.4.7 lifecycle_0.2.0 estimability_1.3
[85] data.table_1.13.6 insight_0.12.0 lmom_2.8
[88] R6_2.5.0 bookdown_0.21 gridExtra_2.3
[91] rio_0.5.16 gld_2.6.2 distill_1.2
[94] boot_1.3-25 MASS_7.3-53 assertthat_0.2.1
[97] rprojroot_2.0.2 withr_2.4.1 mgcv_1.8-33
[100] bayestestR_0.8.2 expm_0.999-6 hms_1.0.0
[103] grid_4.0.3 class_7.3-17 minqa_1.2.4
[106] rmarkdown_2.6 downlit_0.2.1 lubridate_1.7.9.2
[109] base64enc_0.1-3 Caso fique interessado em como montar tabelas para publicações, veja o nosso conteúdo auxiliar de tabelas para publicação.
↩︎Caso fique interessado em como montar tabelas para publicações, veja o nosso conteúdo auxiliar de tabelas para publicação.
↩︎para saber mais sobre regressão linear e seus pressupostos veja o conteúdo do tutorial sobre regressão linear↩︎