Regressão Linear

Como mensurar efeitos de diversas variáveis independentes sobre uma variável dependente contínua.

Muitas vezes precisamos de técnicas que tolerem varíaveis independentes contínuas. Não conseguimos usar ANOVA pois as variáveis independentes são discretas e representam grupos distintos de observações (uma variável independente – Anova Unidireacional, duas variáveis independentes – Anova Bidirecional, etc.). Muito menos teste \(t\), pois segue o mesmo princípio da ANOVA mas se restringindo a apenas dois grupos, ou seja, apenas variável independente categórica binária. Para isso temos a técnica de Regressão Linear.

Regressão Linear é a técnica preferida do autor 1

Regressão linear permite com que você use uma ou mais variáveis discretas ou contínuas como variáveis independentes e mensurar o poder de associação com a variável dependente, que deve ser contínua¹.

Interpretações

Para compreender regressão linear podemos usar de três interpretações distintas mas complementares:

• Interpretação Geométrica: Regressão como uma reta.
• Interpretação Matemática: Regressão como otimização.
• Interpretação Estatística: Regressão como poder de associação entre variáveis controlando para diversos outros efeitos.

Essas interpretações descrevem a mesma técnica mas sob aspectos diferentes. Lembra um pouco a metáfora dos sete sábios e o elefante (figura 1):

Numa pequena cidade viviam sete sábios cegos. Por conta de sua reconhecida sabedoria, as pessoas os procuravam em busca de conselhos para solução de seus problemas. Apesar de amigos, os sábios mantinham entre si uma competitividade acirrada, discutiam o tempo todo tentando provar quem era o mais sábio. Um dia trouxeram um elefante para a cidade. Os cegos rodearam o elefante para tocá-lo. Cada um pegou em uma parte distinta do animal e o descreve de acordo com aquela parte. Eles estão descrevendo o mesmo animal, mas cada um descrevendo apenas uma parte e pensando que é o todo. Eles estão, ao mesmo tempo, certos e errados².

Figure 1: Os Sete Sábios e o Elefante. Figura de https://nsjour.wordpress.com/2012/10/21/seven-blind-men-and-the-elephant/

Interpretação Geométrica

Imagine que seus dados são pontos que vivem em um espaço multidimensional. A regressão é uma técnica para encontrar a melhor reta³ entre o conjunto de dados levando em conta todas as observações.

Isto é valido para qualquer espaço multidimensional, até para além de 3-D. Vamos mostrar um exemplo em 2-D da relação entre x e y⁴, mas isto poder ser estendido para a relação x1, x2, … e y.

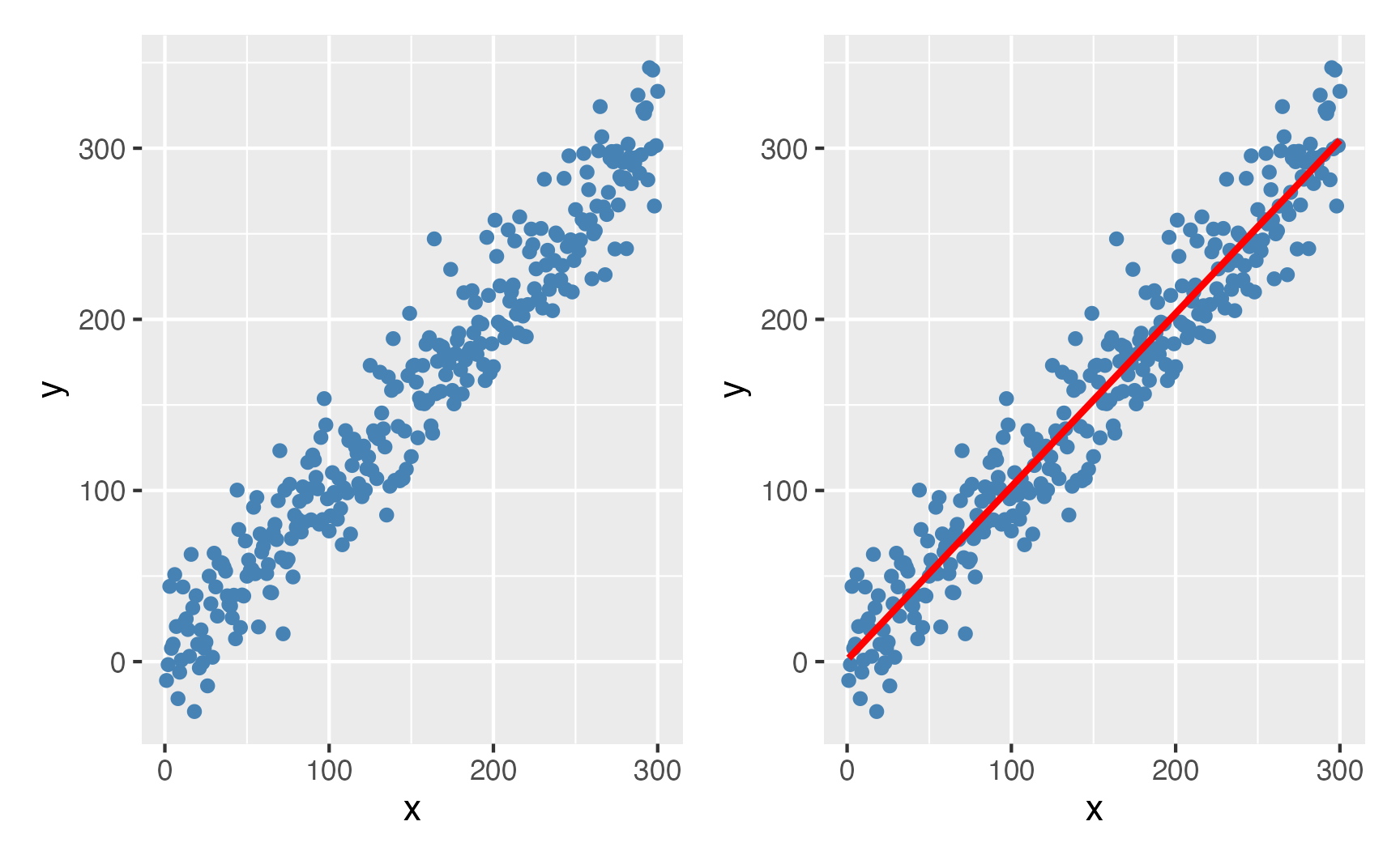
Figure 2: Uma relação entre variáveis representada por uma reta de tendência

Vejam que regressão linear usando apenas uma variável dependente e uma variável independente é a mesma coisa que que correlação⁵.

Interpretação Matemática

A interpretação matemática é vista como uma otimização: encontrar a melhor reta entre os pontos que minimiza o erro quadrático médio (mean squared error – MSE). Ao escolhermos a melhor reta, devemos escolher a melhor reta que minimiza as distâncias entre os pontos, sendo que podemos errar para mais ou para menos. Para evitarmos que os erros se cancelem, precisamos eliminar o sinal negativo de alguns erros e convertê-los para valores positivos. Para isso, pegamos todas os erros (diferenças entre o valor previsto pela reta e o valor verdadeiro) e elevamos ao quadrado (assim todo número negativo se tornará positivo e todo positivo se manterá positivo)⁶. Portanto, a regressão se torna a busca do menor valor de uma função erro (MSE)⁷.

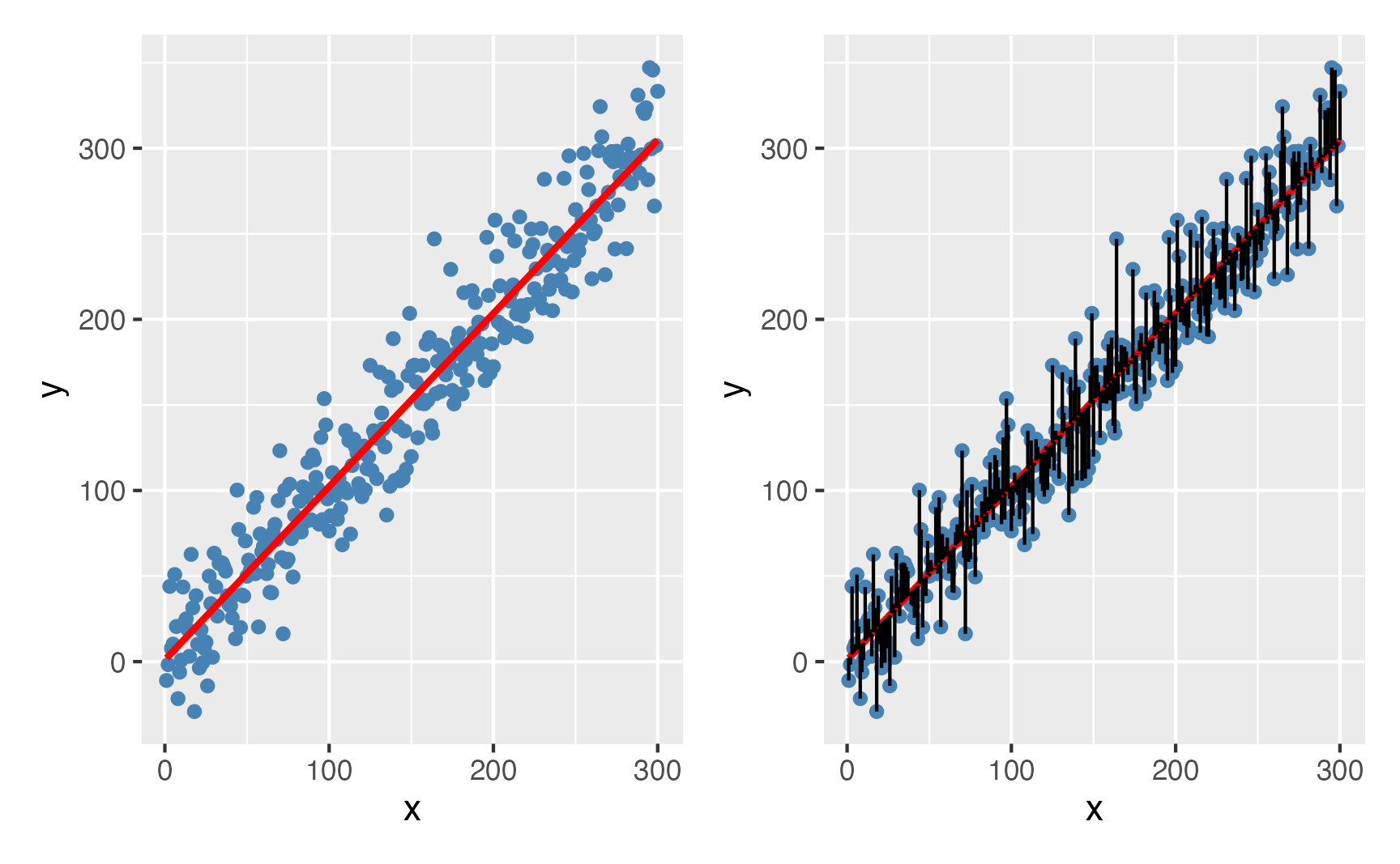
Figure 3: A melhor reta que minimiza a distância dos erros

Interpretação Estatística

A regressão linear usando uma única variável independente contínua se torna exatamente uma correlação⁸. Agora quando empregamos mais de uma variável independente, a interpretação da regressão se torna: “O efeito de X em Y mantendo Z fixo”. Isto quer dizer que a regressão linear controla os efeitos das diferentes variáveis independentes ao calcular o efeito de uma certa variável independente. Esta é o que chamamos de interpretação estatística da regressão linear.

Por exemplo, digamos que você esteja em busca dos fatores que acarretam ataque cardíaco. Você coleta dados de pessoas que quantifiquem as seguintes variáveis: sono, stress, tabagismo, sedentarismo, entre outros… A regressão te permite mensurar o efeito de qualquer uma dessas variáveis na prevalência de ataque cardíaco controlando para outros efeitos. Em outras palavras, é possível mensurar o efeito de stress em ataque cardíaco, mantendo fixo os efeitos de sono, tabagismo, sedentarismo, etc… Isso permite você isolar o efeito de uma variável sem deixar que outras variáveis a influenciem na mensuração da sua relação com a variável dependente (no nosso caso: ataque cardíaco).

História da Regressão

O termo “regressão” foi cunhado por Francis Galton no século XIX para descrever um fenômeno biológico. O fenômeno era que as alturas dos descendentes de ancestrais altos tendem a regredir para uma média normal (um fenômeno também conhecido como regressão em direção à média) (Galton, 1890). Para Galton, a regressão tinha apenas este significado biológico (Galton, 1877), mas seu trabalho foi posteriormente estendido por Udny Yule (Yule, 1897) e Karl Pearson (Pearson, 1903) para um contexto estatístico mais geral.

Figure 4: Da esquerda para direita: Francis Galton, Karl Pearson e Udny Yule – Figuras de https://www.wikipedia.org

Pressupostos da Regressão Linear

Para interpretar os resultados de uma regressão como uma quantidade estatística significativa que mede os relacionamentos do mundo real, precisamos contar com uma série de suposições clássicas. Os quatro principais pressupostos da regressão são:

1. Independência dos Dados: o valor de uma observação não influencia ou afeta o valor de outras observações. Este é o pressuposto clássico de todas as técnicas abordadas até agora.
2. Linearidade dos Dados: a relação entre as variáveis independentes e a variável dependente é considerada linear (quanto mais/menos de uma, mais/menos de outra). Linearidade dos Dados pode ser verificada graficamente observando a dispersão dos resíduos com os valores previstos pela regressão.
3. Independência dos Erros / Resíduos: os erros (também chamados de resíduos) não devem possuir correlação. Este pressuposto pode ser testado pelo teste de Durbin-Watson e observando o gráfico quantil-quantil (Q-Q) dos resíduos padronizados.
4. Homogeneidade de Variância dos Erros / Resíduos: os erros devem ter média zero e desvio padrão constante ao longo das observações. Similar ao teste de Levene, mas aplicado aos resíduos da regressão. Pode ser testado usando o Teste de Breusch-Pagan.
5. Ausência de Multicolinearidade: multicolinearidade é a ocorrência de alta correlação entre duas ou mais variáveis independentes e pode levar a resultados distorcidos. Em geral, a multicolinearidade pode fazer com que os intervalos de confiança se ampliem, ou até mudar o sinal de influência das variáveis independentes (de positivo para negativo, por exemplo). Portanto, as inferências estatísticas de uma regressão com multicolinearidade não são confiáveis. Pode ser testado usando o Fator de Inflação de Variância (Variance Inflation Factor – VIF).

Como aplicar uma Regressão Linear no R

Para exemplificar as regressões nesse tutorial, usaremos o dataset já incluído no R mtcars (Henderson & Velleman, 1981). mtcars é uma base de dados extraída da revista americana sobre carros Motor Trend US de 1974. Possui 32 observações de carros e 11 variáveis:

• mpg: Milhas por Galão (consumo)
• cyl: Número de cilíndros
• disp: Cilindrada (em polegada cúbica)
• hp: Cavalos de Potência (HP)
• drat: Relação do eixo traseiro
• wt: Peso em (1,000 libras)
• qsec: Tempo que atinge 400m (1/4 de milha)
• vs: Motor (0 = Forma em V, 1 = Reto)
• am: Transmissão (0 = Automático, 1 = Manual)
• gear: Número de marchas
• carb: Número de carburadores

library(skimr)
data(mtcars)
skim(mtcars)

Table 1: Data summary

Name	mtcars
Number of rows	32
Number of columns	11
_______________________
Column type frequency:
numeric	11
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
mpg	0	1	20.09	6.03	10.4	15.4	19.2	22.8	33.9	▃▇▅▁▂
cyl	0	1	6.19	1.79	4.0	4.0	6.0	8.0	8.0	▆▁▃▁▇
disp	0	1	230.72	123.94	71.1	120.8	196.3	326.0	472.0	▇▃▃▃▂
hp	0	1	146.69	68.56	52.0	96.5	123.0	180.0	335.0	▇▇▆▃▁
drat	0	1	3.60	0.53	2.8	3.1	3.7	3.9	4.9	▇▃▇▅▁
wt	0	1	3.22	0.98	1.5	2.6	3.3	3.6	5.4	▃▃▇▁▂
qsec	0	1	17.85	1.79	14.5	16.9	17.7	18.9	22.9	▃▇▇▂▁
vs	0	1	0.44	0.50	0.0	0.0	0.0	1.0	1.0	▇▁▁▁▆
am	0	1	0.41	0.50	0.0	0.0	0.0	1.0	1.0	▇▁▁▁▆
gear	0	1	3.69	0.74	3.0	3.0	4.0	4.0	5.0	▇▁▆▁▂
carb	0	1	2.81	1.62	1.0	2.0	2.0	4.0	8.0	▇▂▅▁▁

Para aplicar uma regressão linear no R usamos a função lm() (linear model) padrão do R. Sua funcionalidade é muito similar à outras funções que já vimos de teste de hipótese, sendo que é necessário fornecer dois argumentos:

1. Fórmula designando a variável dependente e a(s) variável(eis) independente(s) designada pela seguinte síntaxe: dependente ~ independente_1 + independente_2 + ....
2. O dataset no qual deverá ser encontradas as variáveis presentes na fórmula.

Começaremos com um exemplo simples de regressão do mtcars usando como variável independente mpg e variáveis independentes hp e wt. Podemos inspecionar o resultado de uma regressão linear com a função summary().

modelo_simples <- lm(mpg ~ hp + wt, data = mtcars)
summary(modelo_simples)

Call:
lm(formula = mpg ~ hp + wt, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-3.941 -1.600 -0.182  1.050  5.854 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept) 37.22727    1.59879   23.28 < 0.0000000000000002 ***
hp          -0.03177    0.00903   -3.52               0.0015 ** 
wt          -3.87783    0.63273   -6.13            0.0000011 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.6 on 29 degrees of freedom
Multiple R-squared:  0.827, Adjusted R-squared:  0.815 
F-statistic: 69.2 on 2 and 29 DF,  p-value: 0.00000000000911

Interpretação dos Coeficientes

Na saída de summary() podemos ver que são produzidos os coeficientes da regressão na coluna Estimate, associados ao respectivos desvio padrão dos resíduos Std. Error e \(p\)-valores Pr(>|t|). Importante destacar que a hipótese nula dos coeficientes da regressão é de que “os coeficientes são nulos/zeros”, então os \(p\)-valores devem ser interpretados como a probabilidade de observamos valores de coeficientes tão extremos dado que a hipótese nula é verdadeira. Para facilitar, o R informa com asteriscos quais variáveis possuem coeficientes estatisticamente significantes: * para \(p < 0.05\), ** para \(p < 0.01\), e *** para \(p < 0.001\).

Os coeficientes de objetos lm devem ser interpretados em escala bruta na qual o acréscimo de 1 unidade da variável independente gera o aumento de <coeficiente> unidade(s) da variável dependente. No nosso exemplo, a cada acréscimo de 1 hp, mpg reduz em -0.03; e a cada acréscimo de 1 wt, mpg reduz em -3.88. Além disso, a regressão linear controla os efeitos de outras variáveis independente. Então o impacto de hp em mpg no nosso exemplo controla o efeito de wt, matendo-o fixo ao calcular o coeficiente de hp.

O coeficiente (Intercept) é o que chamamos de constante (intercept) da regressão. A constante representa o valor médio da variável dependente quando todas as variáveis independentes possuem valor nulo (zero). No nosso exemplo, as observações possuem em média 37.23 mpg quando tanto hp e wt são 0.

Note que podemos produzir intervalos de confiança usando a função padrão do R confint() inserindo como argumento um objeto lm. confint() como padrão produz intervalos de confiança 95%.

confint(modelo_simples)

            2.5 % 97.5 %
(Intercept) 33.96 40.497
hp          -0.05 -0.013
wt          -5.17 -2.584

Variáveis Qualitativas

Além de variáveis independentes quantitativas, regressão linear também permite utilizarmos variáveis qualitativas (discretas) como variáveis independentes.

Vamos estender o nosso modelo simples adicionando a variável am. Note que vamos convertê-la para qualitativa (factor) usando a função padrão do R as.factor(), Isto é necessário para que o R interprete am como fator (nomenclatura do R para variáveis qualitativas).

modelo_quali <- mtcars %>%
  mutate(am = as.factor(am)) %>%
  lm(mpg ~ hp + wt + am, data = .)
summary(modelo_quali)

Call:
lm(formula = mpg ~ hp + wt + am, data = .)

Residuals:
   Min     1Q Median     3Q    Max 
-3.422 -1.792 -0.379  1.225  5.532 

Coefficients:
            Estimate Std. Error t value         Pr(>|t|)    
(Intercept) 34.00288    2.64266   12.87 0.00000000000028 ***
hp          -0.03748    0.00961   -3.90          0.00055 ***
wt          -2.87858    0.90497   -3.18          0.00357 ** 
am1          2.08371    1.37642    1.51          0.14127    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.5 on 28 degrees of freedom
Multiple R-squared:  0.84,  Adjusted R-squared:  0.823 
F-statistic:   49 on 3 and 28 DF,  p-value: 0.0000000000291

Quando convertemos uma variável para fator, o R rotula os diferentes níveis (levels) conforme ordem alfabética. Portanto, no nosso exemplo, am possui 2 níveis: 0 e 1 (apesar de serem números, na conversão o R usa uma ordem crescente para dígitos). Numa regressão linear que possua variáveis qualitativas codificadas como fatores, o R usará o primeiro nível do fator (no nosso caso am0) como referência. Portanto a interpretação do coeficiente am1 deve ser a seguinte: observações com am = 1 possuem um acréscimo em média de 2.08 mpg. Note também que a variável am não possui significância estatística para a diferença entre o nível de referência am0 e o nível am1 com \(p = 0.14\). É possível verificar os diferentes níveis das variáveis qualitativas de um objeto lm acessando seu atributo xlevels.

modelo_quali$xlevels

$am
[1] "0" "1"

Efeitos Principais e Efeitos de Interação

Todos os modelos de regressão que mostramos até aqui usaram apenas efeitos principais. Mas podemos também mostrar efeitos de interação (também chamados de efeitos de moderação) entre duas variáveis. Similar ao exposto no tutorial sobre ANOVA, podemos incluir dois tipos de efeitos na regressão linear:

• Efeitos principais: efeito de uma (ou mais) variável(is) independente(s) em uma variável dependente. Chamamos esses efeitos de aditivos pois podem ser quebrados em dois efeitos distintos e únicos que estão influenciando a variável dependente.
• Efeitos de interações: quando o efeito de uma (ou mais) variável(is) independente(s) em uma variável dependente é afetado pelo nível de outras variável(is) independente(s). Efeitos de interação não são aditivos pois podem ser quebrados em dois efeitos distintos e únicos que estão influenciando a variável dependente. Há uma interação entre as variáveis independentes.

Veja na figura 5 uma representação gráfica da interação entre am e cyl. Note que a interação é observada pela diferença de inclinações entre as linhas coloridas que representam os diferentes valores de cyl⁹.

mtcars %>%
  mutate(across(c(am, cyl), as.factor)) %>%
  group_by(am, cyl) %>%
  summarise(mpg = mean(mpg)) %>%
  ggplot(aes(x = am, y = mpg, color = cyl)) +
  geom_line(aes(group = cyl)) +
  geom_point() +
  scale_colour_brewer(palette = "Set1")

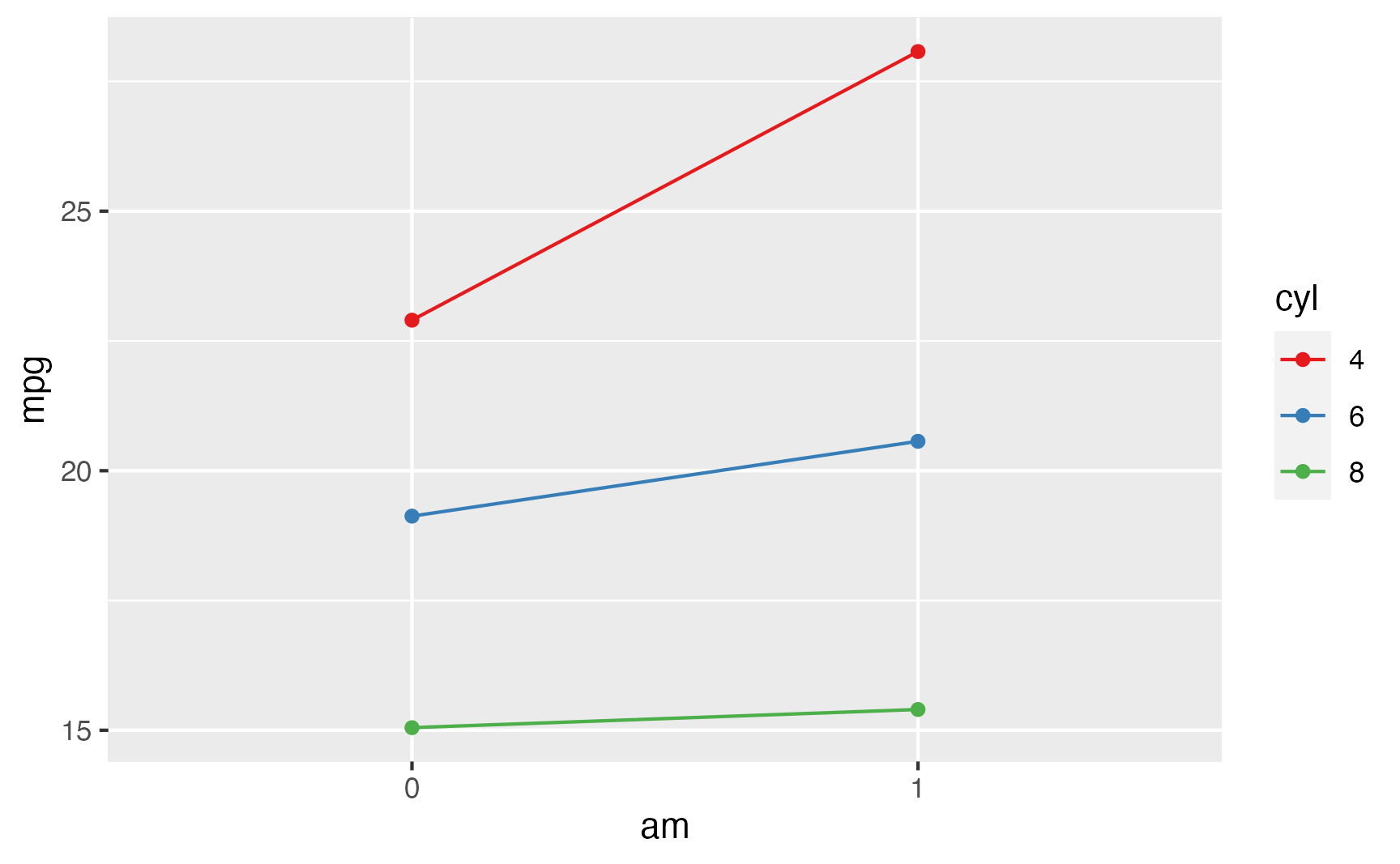
Figure 5: Interação entre am e cyl do dataset mtcars

Para incluirmos efeitos de interações entre duas variáveis independentes em regressões lineares, incluímos na fórmula entre as duas variáveis um sinal de multiplicação¹⁰ * indicando que as duas variáveis devem ser usadas como efeitos principais e também de interação na análise.

modelo_interacao <- lm(mpg ~ hp + wt + cyl * am, data = mtcars)
summary(modelo_interacao)

Call:
lm(formula = mpg ~ hp + wt + cyl * am, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-4.080 -1.481 -0.769  1.368  5.240 

Coefficients:
            Estimate Std. Error t value       Pr(>|t|)    
(Intercept)  34.6530     3.2428   10.69 0.000000000052 ***
hp           -0.0164     0.0148   -1.11          0.278    
wt           -2.7220     0.9090   -2.99          0.006 ** 
cyl          -0.6646     0.5764   -1.15          0.259    
am            6.3264     3.8041    1.66          0.108    
cyl:am       -0.9000     0.6552   -1.37          0.181    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.5 on 26 degrees of freedom
Multiple R-squared:  0.859, Adjusted R-squared:  0.832 
F-statistic: 31.7 on 5 and 26 DF,  p-value: 0.000000000279

A interpretação do coeficiente cyl:am é a seguinte: cyl (ou am) modera positivamente a relação entre am (ou cyl) e mpg. Note que o \(p\)-valor de cyl:am não possui significância estatística (\(p = 0.181\)).

Efeitos Não-Lineares

Podemos também incluir efeitos não-lineares em modelos de regressão linear. Uma relação não-linear é aquela que a representação entre as variáveis não pode ser representada de maneira fidedigna de maneira linear (com uma reta, mas sim com uma curva). Na ciência, há diversos fenômenos que não podem ser representados linearmente. Na figura @(fig:mtcars-poly) é possível ver a relação entre hp e mpg: a linha vermelha mostra uma tendência linear e a linha azul uma tendência não-linear.

mtcars %>%
  ggplot(aes(hp, mpg)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, color = "Red") +
  geom_smooth(method = "lm", formula = y ~ poly(x, 2), se = FALSE, color = "Blue")

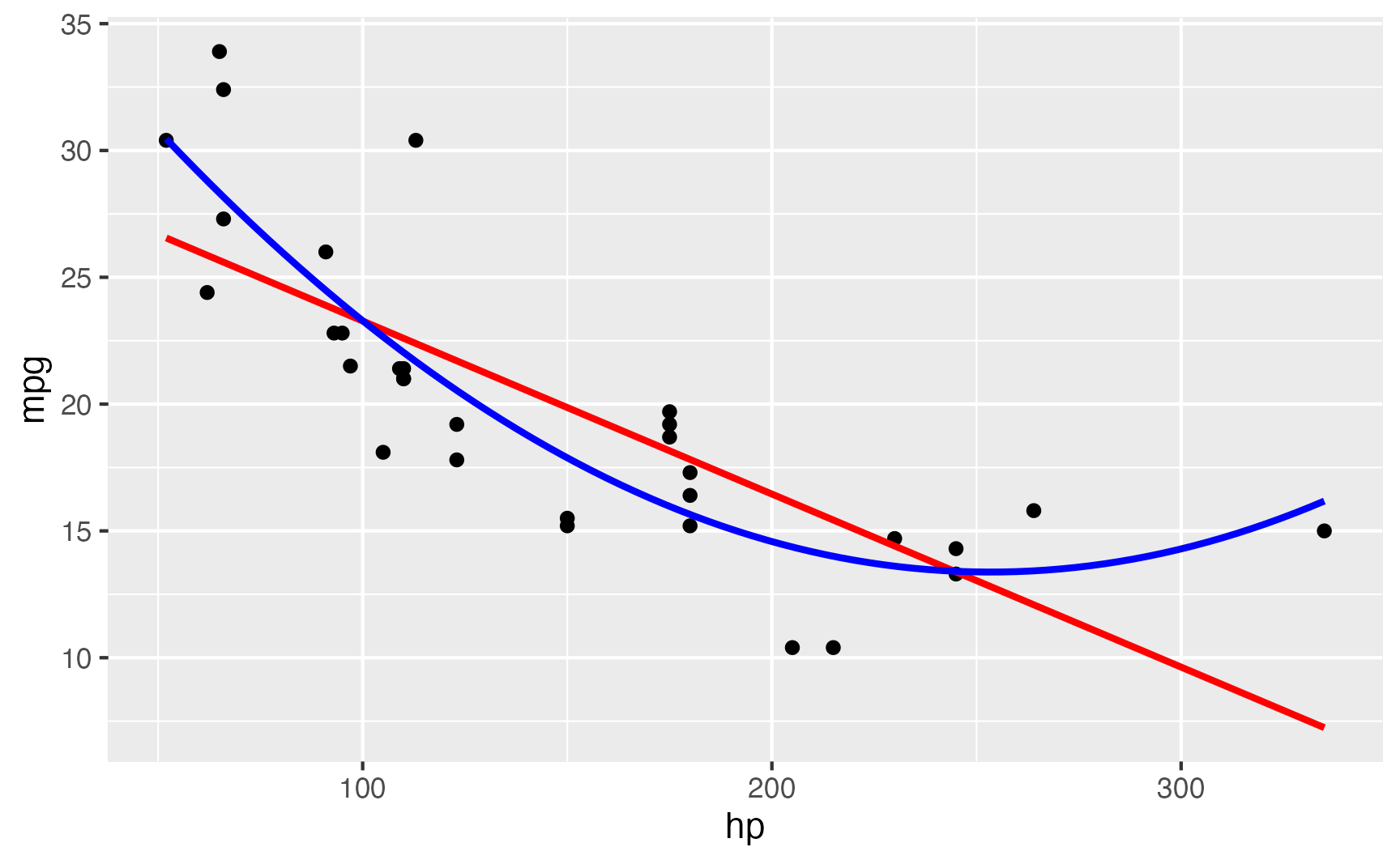
Figure 6: Relação Não-Linear entre hp e mpg do dataset mtcars

Para inserirmos efeitos não-lineares, incluímos na fórmula a função poly() com as variáveis que desejamos efeitos não-linares. A função poly() gera polinômios das variáveis conforme o grau especificado. No nosso exemplo abaixo, usaremos um polinômio de grau 2 (efeito quadrático).

modelo_naolinear <- lm(mpg ~ poly(hp, 2) + wt, data = mtcars)
summary(modelo_naolinear)

Call:
lm(formula = mpg ~ poly(hp, 2) + wt, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-3.059 -1.260 -0.509  0.703  4.980 

Coefficients:
             Estimate Std. Error t value          Pr(>|t|)    
(Intercept)    29.839      2.209   13.51 0.000000000000087 ***
poly(hp, 2)1  -15.172      3.398   -4.46           0.00012 ***
poly(hp, 2)2    6.900      2.763    2.50           0.01867 *  
wt             -3.030      0.674   -4.50           0.00011 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.4 on 28 degrees of freedom
Multiple R-squared:  0.858, Adjusted R-squared:  0.843 
F-statistic: 56.6 on 3 and 28 DF,  p-value: 0.00000000000529

Veja que ambos os coeficientes poly(hp, 2)1 (que deve ser interpretado como \(\text{hp}^1\)) e poly(hp, 2)2 (que deve ser interpretado como \(\text{hp}^2\)) possuem significância estatística (\(p < 0.05\)).

Visualização de Regressão Linear

Uma vez que as variáveis dos modelos de regressão começam a ficar numerosas, as visualizações podem ajudar. Em especial, gostamos bastante da biblioteca {sjPlot} (Lüdecke, 2020) e sua função plot_model(). Como padrão, a função plot_model() produz um gráfico de floresta (forest plot) e também conhecido como blobograma no qual podemos visualizar as variáveis no eixo vertical e o tamanho do efeito, os coeficientes, no eixo horizontal. Além disso, coeficientes positivos são representados com a cor azul e negativos em vermelho; e os intervalos de confiança 95% como uma linha ao redor do valor médio do coeficiente (ponto). Ao especificarmos o tipo como "std" em plot_model(), o gráfico de floresta produzido utiliza os valores padronizados em desvios padrões. Veja um exemplo na figura 7: no lado esquerdo temos o gráfico de floresta para coeficientes brutos e no lado direto para coeficientes padrões.

library(sjPlot)
forest_raw <- plot_model(modelo_quali)
forest_std <- plot_model(modelo_quali, type = "std")
forest_raw + forest_std + plot_layout(nrow = 1, widths = 1)

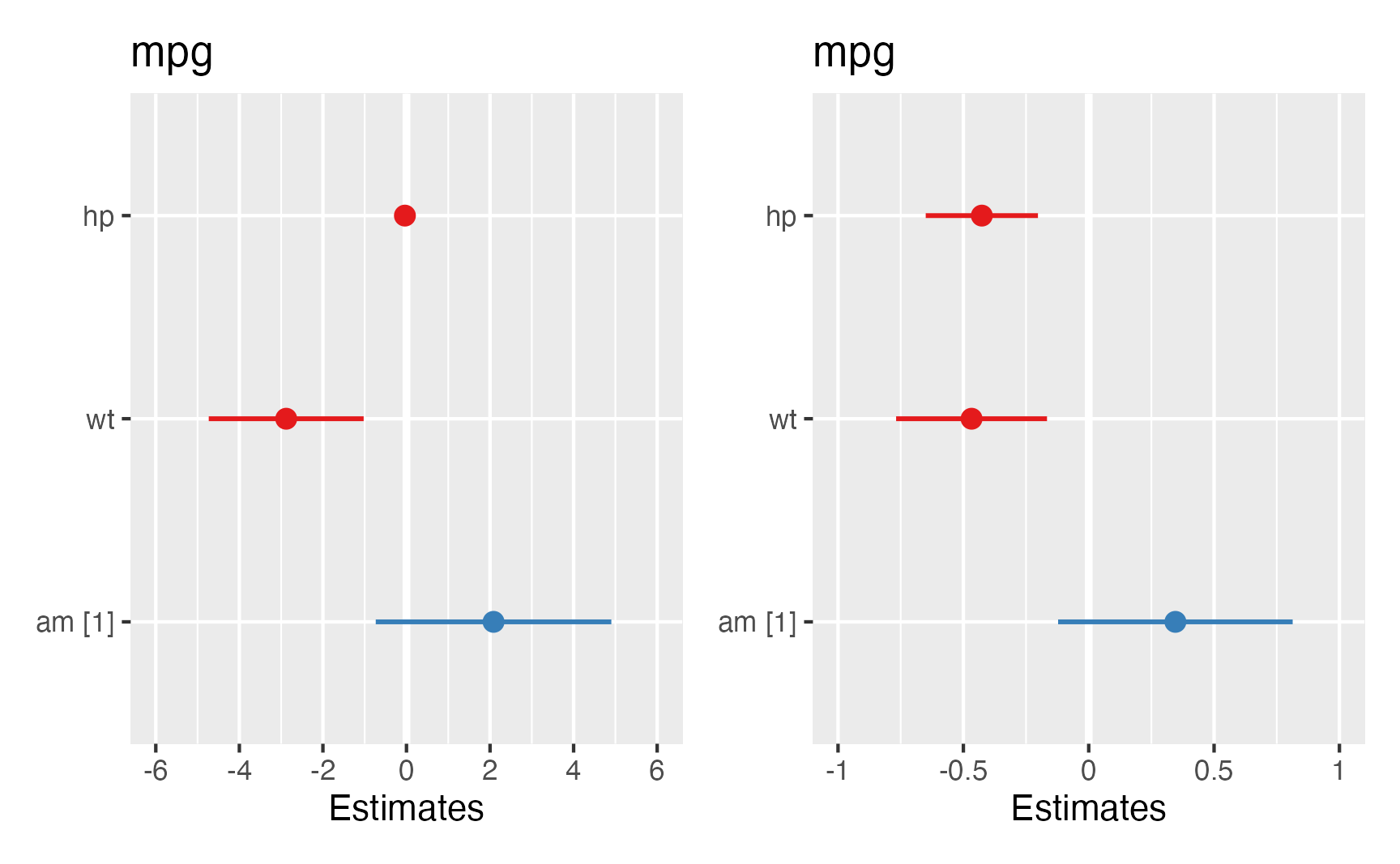
Figure 7: Gráfico de Floresta dos Coeficientes de uma Regressão Linear

Caso queira mais opções de visualizações para modelos de regressão não deixe de conferir o site da biblioteca {sfPlot}.

Verificação de Pressupostos

A verificação de pressupostos se divide em visualizações e testes estatísticos.

Visualizações

Para visualização diagnóstica de modelos de regressão linear temos a opção plot() padrão do R para modelos lm. Mas essa visualização não é interessante pois usa o sistema padrão do R para visualizações ao invés do sistema {ggplot2} (Wickham, 2016) que permite maiores configurações e controle. Para visualizar diagnósticos de objetos lm usando o sistema {ggplot2} recomendamos a biblioteca {ggfortify} (Horikoshi & Tang, 2018).

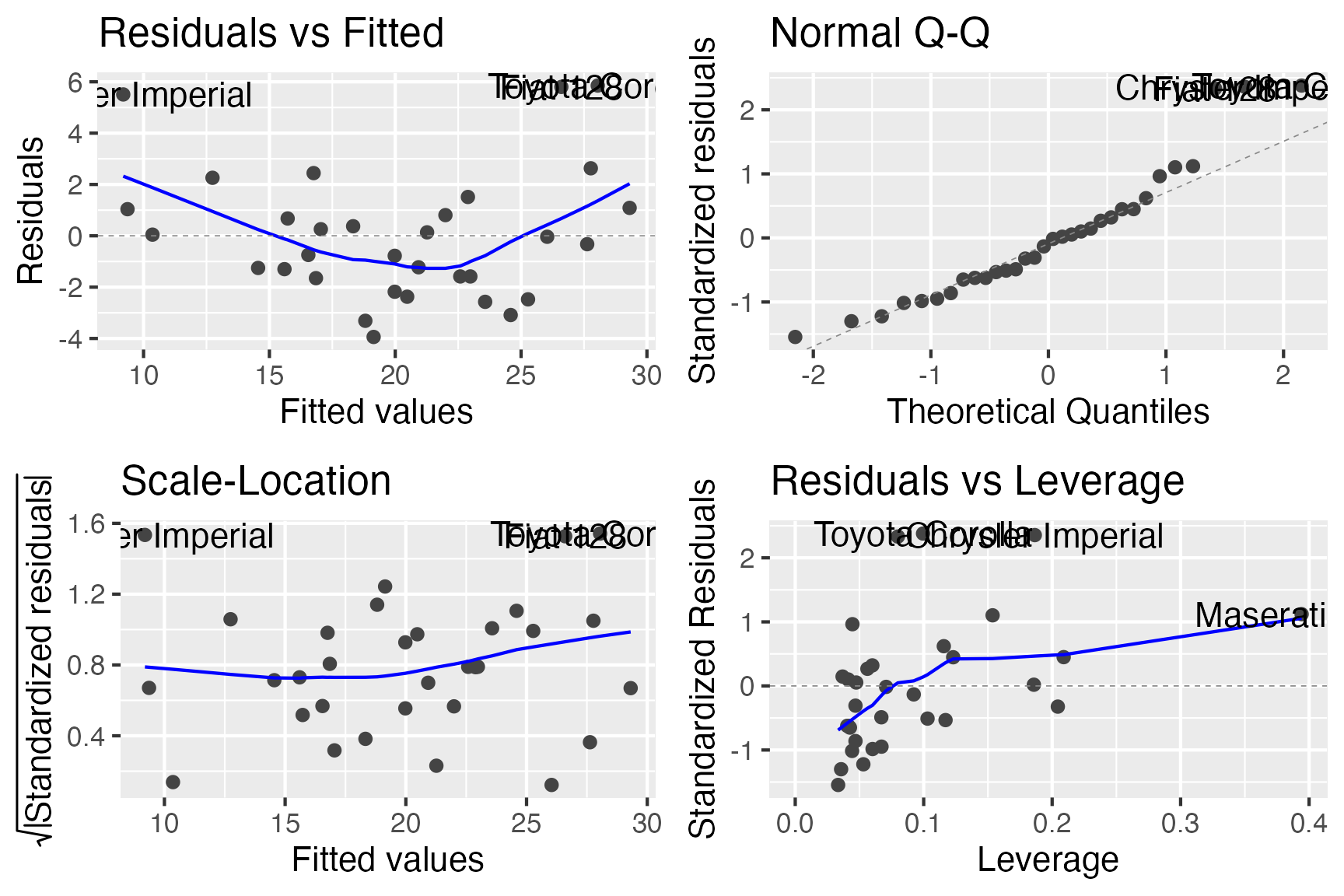
A a função autoplot() da biblioteca {ggfortify} mostra os resíduos em quatro gráficos diferentes:

1. Residuals vs Fitted (Resíduos vs Valores Previstos): utilizado para verificar os pressupostos de linearidade. Uma linha horizontal, sem padrões distintos é um indicativo de uma relação linear, o que indica que o pressuposto não foi violado.
2. Normal Q-Q (Q-Q dos Resíduos): utilizado para verificar se os resíduos estão normalmente distribuídos. Se os pontos residuais seguirem a linha reta tracejada, indica que o pressuposto de independência dos resíduos não foi violado.
3. Scale-Location (Resíduos “Studentizados” vs Valores Previstos): utilizado para verificar a homogeneidade da variância dos resíduos (homocedasticidade). Uma linha horizontal com pontos igualmente espalhados é uma boa indicação que o pressuposto não foi violado. Usa o formato “Studentizado” dos resíduos que é o quociente resultante da divisão de um resíduo por uma estimativa de seu desvio padrão. É uma forma de estatística \(t\) de Student, com a estimativa de erro variando entre os pontos.
4. Residuals vs Leverage (Resíduos vs Influências): Utilizado para identificar casos influentes, ou seja, valores extremos que podem influenciar os resultados da regressão quando incluídos ou excluídos da análise.

Veja um exemplo de visualização diagnóstica do modelo_simples na figura 8. É um bom exemplo que demonstra diversas patologias (problemas) do modelo. Os resíduos (gráfico superior esquerdo) possui um padrão evidente, o gráfico Q-Q dos resíduos (gráfico superior direito) evidencia algumas observações com resíduos que ferem o pressuposto de independência dos resíduos, e por fim possuímos uma observação extremamente influente (gráfico inferior direito – Maserati B) que talvez prejudique as inferências do modelo.

library(ggfortify)
autoplot(modelo_simples)

Figure 8: Diagnósticos de Regressão Linear

Testes Estatísticos

Além de visualizações diagnóstica, podemos realizar diversos testes estatísticos de hipótese nula para verificar se o modelo de regressão linear possui pressupostos violados ou não. Para isso recomendamos a biblioteca {lmtest} (Zeileis & Hothorn, 2002).

Teste de Breusch-Pagan

O teste de Breusch-Pagan(Breusch & Pagan, 1979; Cook & Weisberg, 1983) usado para testar o pressuposto da independência dos resíduos possui como hipótese nula que “as variâncias de erro são todas iguais” e como hipótese alternativa que “as variâncias de erro são uma função multiplicativa de uma ou mais variáveis.” Recomendamos que usem os resíduos “Studentizados” (quociente resultante da divisão de um resíduo por uma estimativa de seu desvio padrão – uma forma de estatística \(t\) de Student, com a estimativa de erro variando entre os pontos) no teste de Breusch-Pagan (Koenker, 1981). A função bptest() da biblioteca {lmtest} aceita como argumento um modelo de regressão linear (objeto lm) e já possui como padrão resíduos “Studentizados.” Caso queira usar resíduos brutos indique o argumento studentize como FALSE.

library(lmtest)
bptest(modelo_simples)

    studentized Breusch-Pagan test

data:  modelo_simples
BP = 0.9, df = 2, p-value = 0.6

Note que o \(p\)-valor do Teste de Breusch-Pagan para o modelo_simples é 0.6, demonstrando fortes evidências em favor da não-rejeição da hipótese nula de dependência dos resíduos.

Teste de Durbin-Watson

O teste de Durbin-Watson (Durbin & Watson, 1950, 1951) é um teste estatístico usado para detectar a presença de autocorrelação dos resíduos de um modelo de regressão e testa o pressuposto da homogeneidade de variância dos resíduos. Possui como hipótese nula que os “erros são serialmente não correlacionados.” A função dwtest() da biblioteca {lmtest} aceita como argumento um modelo de regressão linear (objeto lm).

dwtest(modelo_simples)

    Durbin-Watson test

data:  modelo_simples
DW = 1, p-value = 0.02
alternative hypothesis: true autocorrelation is greater than 0

Note que o \(p\)-valor do Teste de Durbin-Watson para o modelo_simples é menor que 0.05, indicando a rejeição da hipótese nula de não-correlação entre os resíduos, violando o pressuposto da homogeneidade de variância dos resíduos.

Multicolinearidade

Multicolinearidade é a ocorrência de alta correlação entre duas ou mais variáveis independentes e pode levar a resultados distorcidos. Em geral, a multicolinearidade pode fazer com que os intervalos de confiança se ampliem, ou até mudar o sinal de influência das variáveis independentes (de positivo para negativo, por exemplo). Portanto, as inferências estatísticas de uma regressão com multicolinearidade não são confiáveis. Pode ser testado usando o Fator de Inflação de Variância (Variance Inflation Factor – VIF).

Os VIFs medem o quanto da variância de cada coeficiente de regressão do modelo estatístico se encontra inflado em relação à situação em que as variáveis independentes não estão correlacionadas. Valores aceitáveis de VIF são menores que 10 (Hair et al., 1998). Para calcular os VIFs de uma modelo lm use a função vif() da biblioteca {car} (Fox & Weisberg, 2019).

library(car)
vif(modelo_simples)

 hp  wt 
1.8 1.8 

Note que os valores de VIFs para as variáveis independentes do modelo_simples estão todos dentro do limite aceitável (\(<10\)), demonstrando ausência de multicolinearidade e evidenciando que o pressuposto não foi violado.

\(R^2\) e \(R^2\) ajustado

O leitor curioso e atencioso talvez tenha percebido que não comentamos uma métrica dos modelos de regressão: R-quadrado (\(R^2\)) e R-quadrado ajustado (\(R^2\) ajustado).

O \(R^2\) também conhecido como coeficiente de determinação representa a proporção da variabilidade na variável dependente prevista¹¹ pelas variáveis independentes. É uma métrica que quantifica o poder preditivo de um modelo de regressão.

Já o \(R^2\) ajustado inclui uma pequena penalidade pelo número de variáveis independentes usada no modelo de regressão. Conforme você adiciona variáveis independentes à um modelo de regressão, o seu \(R^2\) sempre aumentará, mas o \(R^2\) ajustado somente aumentará se você adicionar variáveis independentes úteis ao modelo (variáveis que aumentem o \(R^2\) um valor maior que a penalidade pela sua inclusão).

summary(modelo_simples)

Call:
lm(formula = mpg ~ hp + wt, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-3.941 -1.600 -0.182  1.050  5.854 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept) 37.22727    1.59879   23.28 < 0.0000000000000002 ***
hp          -0.03177    0.00903   -3.52               0.0015 ** 
wt          -3.87783    0.63273   -6.13            0.0000011 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.6 on 29 degrees of freedom
Multiple R-squared:  0.827, Adjusted R-squared:  0.815 
F-statistic: 69.2 on 2 and 29 DF,  p-value: 0.00000000000911

Veja que o modelo_simples possui como \(R^2\) um valor de 0.83: isto quer dizer que o modelo_simples possui um poder preditivo de 83% da variância de mpg. Além disso seu \(R^2\) ajustado é que pode ser útil na hora de comparar diferentes modelos que usem o mesmo conjunto de dados mtcars e a mesma variável dependente mpg.

Coeficientes Brutos versus Padronizados

Além de coeficientes brutos, podemos também obter coeficientes padronizados por desvios padrões de regressão linear usando a biblioteca {lm.beta} (Behrendt, 2014). Tal interpretação é vantajosa quando temos variáveis na regressão que possuem medidas diversas e que a comparação não seria tão simples. Os coeficientes padronizados são disponibilizados na coluna Standardized.

library(lm.beta)
modelo_simples_padronizado <- lm.beta(modelo_simples)
summary(modelo_simples_padronizado)

Call:
lm(formula = mpg ~ hp + wt, data = mtcars)

Residuals:
   Min     1Q Median     3Q    Max 
-3.941 -1.600 -0.182  1.050  5.854 

Coefficients:
            Estimate Standardized Std. Error t value
(Intercept) 37.22727      0.00000    1.59879   23.28
hp          -0.03177     -0.36145    0.00903   -3.52
wt          -3.87783     -0.62955    0.63273   -6.13
                        Pr(>|t|)    
(Intercept) < 0.0000000000000002 ***
hp                        0.0015 ** 
wt                     0.0000011 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.6 on 29 degrees of freedom
Multiple R-squared:  0.827, Adjusted R-squared:  0.815 
F-statistic: 69.2 on 2 and 29 DF,  p-value: 0.00000000000911

A interpretação de coeficientes padronizados é quase a mesma que coeficientes padrões, apenas mudando a escala de comparação, que deve ser interpretada em escala padronizada em desvios padrões: o acréscimo de 1 unidade de desvio padrão variável independente gera o aumento de <coeficiente> unidade(s) de desvio padrão(ões) da variável dependente. No nosso exemplo, a cada acréscimo de 1 desvio padrão de hp, mpg reduz em -0.36 desvio padrão; e a cada acréscimo de 1 desvio padrão wt, mpg reduz em -0.63 desvio padrão.

Note que a constante (Intercept) não deve ser usada em escalas padronizada por desvio padrão, por isso que a saída de objetos lm.beta possui valor 0 para a constante (Intercept).

Para gerar intervalos de confiança podemos usar a função confint() para objetos lm.beta da mesma maneira que usamos para objetos lm:

confint(modelo_simples_padronizado)

            2.5 % 97.5 %
(Intercept) -3.27   3.27
hp          -0.38  -0.34
wt          -1.92   0.66

Conexões com o Teste \(t\), ANOVA e Correlações

Todos as técnicas estatísticas que vimos até agora (teste \(t\), ANOVA e correlação) são casos especiais de regressão linear¹². Caso o leitor se interesse aconselhamos a leitura do capítulo 5 de Poldrack (2018) e o excelente tutorial de Lindelov (2019). Caso o leitor queira substituir todos os testes estatísticos pela função lm() veja a tabela abaixo:

Conforme o autor 2, regressão linear é pizza e “tudo acaba em pizza.”

Nome do Teste1	função do R	Modelo de Regressão equivalente no R
P: teste t para Amostras Independentes	t.test(y)	lm(y ~ 1)
N: Teste de Wilcoxon	wilcox.test(y)	lm(signed_rank(y) ~ 1)
P: Teste t para duas Amostras Pareadas	t.test(y1, y2, paired=TRUE)	lm(y2 - y1 ~ 1)
N: Teste de Wilcoxon para duas Amostras Pareadaspairs	wilcox.test(y1, y2, paired=TRUE)	lm(signed_rank(y2 - y1) ~ 1)
P: Correlação de Pearson	cor.test(x, y, method=’Pearson’)	lm(y ~ 1 + x)
N: Correlação de Spearman	cor.test(x, y, method=’Spearman’)	lm(rank(y) ~ 1 + rank(x))
P: Teste t para Duas Amostras não-Pareadas	t.test(y1, y2, var.equal=TRUE)	lm(y ~ 1 + G2)
N: Teste de Mann-Whitney	wilcox.test(y1, y2)	lm(signed_rank(y) ~ 1 + G2)
P: ANOVA Unidirecional	aov(y ~ group)	lm(y ~ 1 + G2 + G3 +…+ GN)
N: Teste de Kruskal-Wallis	kruskal.test(y ~ group)	lm(rank(y) ~ 1 + G2 + G3 +…+ GN)
P: ANOVA Bidirecional com efeitos principais	aov(y ~ group + x)	lm(y ~ 1 + G2 + G3 +…+ GN + x)
P: ANOVA Bidirecional com efeitos de interação	aov(y ~ group * sex)	lm(y ~ 1 + G2 + G3 +…+ GN + S2 + S3 +…+ SK + G2*S2 + G3*S3 + … + GN*SK)
Fonte: adaptado de Lindelov (2019).
1 P: paramétrico - N: não-paramétrico

Técnicas Avançadas de Regressão Linear

Nesta seção apenas apresentaremos alternativas avançadas, não é o foco desse conteúdo introdutório apresentar de maneira detalhada, mas sim de apontar o leitor na direção correta.

• Regressão Robusta
• Regressão Regularizada
• Regressão Aditiva - Modelos Aditivos Generalizados
• Regressão Multinível

Regressão Robusta

Regressão linear não é uma boa alternativa na presença de observações extremas (também chamadas de outliers). O pressuposto de que os erros (ou resíduos) são distribuidos conforme uma distribuição Normal com média 0 faz com que as estimativas de uma regressão linear fiquem instáveis. Para exemplificar isso, vamos fazer uma simulação com 50 observações sendo que 40 observações são distribuídas como uma distribuição Normal e 10 observações são extremas (estão além de dois desvios padrões – \(\pm 2 \times \sigma\)).

library(dplyr)

n_sims <- 50

sims <- tibble(
  x = 1:n_sims,
  y = c(rnorm(floor(4 * n_sims / 5)), sample(c(-4:-3, 3:4), ceiling(n_sims / 5), 1)),
  tipo = c(rep("normal", floor(4 * n_sims / 5)), rep("extrema", ceiling(n_sims / 5)))
) %>%
  sample_frac(1L)  ## Randomize!

A figura 9 mostra um diagrama de pontos (dotplot) da simulação e duas distribuições estimadas com os dados: Normal e \(t\) de Student (graus de liberdade = 3). Devido às observações extremas, a distribuição Normal, para comportar todas as observações, se alarga e achata. Tal achatamento e alargamento não ocorrem na distribuição \(t\) de Student. Isto se traduz em estimativas mais estáveis dos coeficientes da regressão na presença de observações extremas. Por esses motivos, para nós, a melhor a maneira de aplicar um modelo de regressão na presença de observações extremas é por meio de Estatística Bayesiana usando uma distribuição \(t\) de Student como o “motor” de inferência.

O primeiro autor possui um tutorial de Estatística Bayesiana com R e um dos tutoriais é sobre regressão robusta usando distribuição \(t\) de Student.

library(ggplot2)
sims %>%
  ggplot(aes(y, fill = tipo)) +
  geom_dotplot(alpha = 0.5) +
  stat_function(fun = dnorm,
                args = list(mean = mean(sims$y), sd = sd(sims$y)),
                aes(color = "Distribuição\nNormal"), size = 3) +
  stat_function(fun = dt,
                args = list(df = 3),
                aes(color = "Distribuição t\nde Student"), size = 3) +
  scale_fill_brewer("Tipo de Observação", palette = "Set1",
                    guide = guide_legend(ncol = 1, nrow = 2, byrow = TRUE)) +
  scale_colour_brewer("Tipo de Distribuição", palette = "Set3",
                      guide = guide_legend(ncol = 1, nrow = 2, byrow = TRUE)) +
  theme(legend.position = "bottom") +
  ylim(c(0, 0.4))

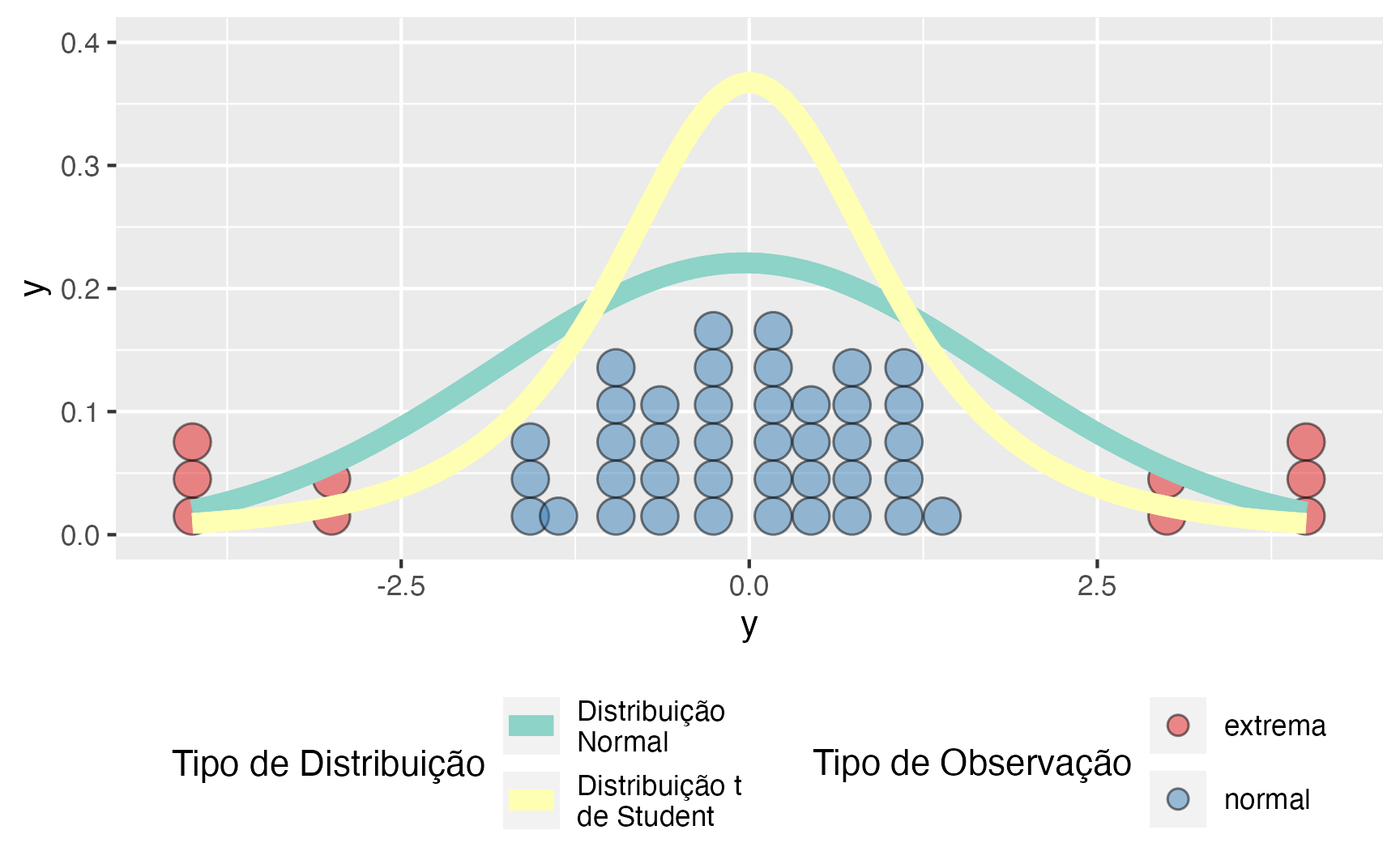
Figure 9: Simulação com Observações Normais e Extremas – Distribuição Normal vs t de Student

Caso o leitor não queria sair do paradigma NHST (afinal em Estatística Bayesiana não temos \(H_0\) nem \(p\)-valores), há duas alternativas de regressão robusta:

1. M-estimação¹³ (Huber, 1964): robusta à observações extremas na variável dependentes, mas não nas independentes.
2. Mínimos quadrados aparados¹⁴ (Rousseeuw, 1984): robusto tanto à observações extremas na variável dependente quanto nas independentes. O método recomendado atualmente por diversas fontes (Rousseeuw & Van Driessen, 2006; Ryan, 2008)

Regressão Regularizada

A regressão regularizada é um tipo de regressão em que as estimativas dos coeficientes são restritas a zero. A magnitude (tamanho) dos coeficientes, bem como a magnitude do termo de erro, são penalizados. Modelos complexos são desencorajados, principalmente para evitar overfitting.

Tipos de regressão regularizada

Dois tipos comumente usados de métodos de regressão regularizados são regressão Ridge e regressão de Lasso.

A regressão de Ridge(Tikhonov, 1943) é uma forma de criar um modelo parcimonioso quando o número de variáveis preditoras em um conjunto excede o número de observações (\(m > p\)) ou quando um conjunto de dados tem forte multicolinearidade (correlações entre variáveis preditoras). A regressão Ridge pertence ao conjunto de ferramentas de regularização L2. A regularização L2 adiciona uma penalidade chamada penalidade L2, que é igual ao quadrado da magnitude dos coeficientes. Todos os coeficientes são reduzidos pelo mesmo fator, de modo que todos os coeficientes permanecem no modelo. A força do termo de penalidade é controlada por um parâmetro de ajuste. Quando este parâmetro de ajuste (\(\lambda\)) é definido como zero, a regressão Ridge é igual à regressão linear. Se \(\lambda = \infty\), todos os coeficientes são reduzidos a zero. A penalidade ideal é, portanto, algo entre \(0\) e \(\infty\).

A regressão Lasso (least absolute shrinkage and selection operator – Lasso) (Efron & Hastie, 2016; Tibshirani, 1996) é um tipo de regressão linear que usa encolhimento (shrinkage). Encolhimento faz com os valores dos coeficientes sejam reduzidos em direção a um ponto central, como a média. Este tipo de redução é muito útil quando você tem altos níveis de muticolinearidade ou quando deseja automatizar certas partes da seleção de modelo, como seleção de variável / eliminação de parâmetro. Lasso usa a regularização L1 que limita o tamanho dos coeficientes adicionando uma penalidade L1 igual ao valor absoluto, ao invés do valor quadrado como L2, da magnitude dos coeficientes. Isso às vezes resulta na eliminação de alguns coeficientes completamente, o que pode resultar em modelos esparsos e seleção de variáveis.

Para usar modelos de regressão regularizada use a biblioteca {glmnet} (Simon, Friedman, Hastie, & Tibshirani, 2011).

Regressão Aditiva - Modelos Aditivos Generalizados

Em estatística, um modelo aditivo generalizado (generalized additive model – GAM) é um modelo linear generalizado no qual a variável de resposta depende linearmente de funções suaves (chamadas de splines) desconhecidas de algumas variáveis preditoras, e o interesse se concentra na inferência sobre essas funções suaves. Os GAMs foram desenvolvidos originalmente por Trevor Hastie e Robert Tibshirani (Hastie, Tibshirani, & others, 1986). Para usar GAMs no R use a biblioteca {gam} (Hastie, 2020).

Regressão Multinível

Modelos multiníveis (também conhecidos como modelos lineares hierárquicos, modelo linear de efeitos mistos, modelos mistos, modelos de dados aninhados, coeficiente aleatório, modelos de efeitos aleatórios, modelos de parâmetros aleatórios ou designs de gráfico dividido) são modelos estatísticos de parâmetros que variam em mais de um nível (Luke, 2019).

Modelos multiníveis são particularmente apropriados para projetos de pesquisa onde os dados dos participantes são organizados em mais de um nível (ou seja, dados aninhados). As unidades de análise geralmente são indivíduos (em um nível inferior) que estão aninhados em unidades contextuais / agregadas (em um nível superior).

Modelos multiníveis geralmente se dividem em três abordagens:

1. Random intercept model: Modelo no qual cada grupo recebe uma constante (intercept) diferente
2. Random slope model: Modelo no qual cada grupo recebe um coeficiente diferente para cada variável independente
3. Random intercept-slope model: Modelo no qual cada grupo recebe tanto uma constante (intercept) quanto um coeficiente diferente para cada variável independente

O primeiro autor possui um tutorial de Estatística Bayesiana com R e um dos tutoriais é sobre regressão multinível.

Para usar modelos multiníveis em R use a biblioteca {lme4} (Bates, Mächler, Bolker, & Walker, 2015).

Comentários Finais

Regressão Linear é a porta de entrada para os modelos lineares. Tais modelos são o “pão-com-manteiga” das ciências sociais aplicadas, usado extensamente tanto em relatórios técnicos quanto na literatura científica, assim como tanto em contextos profissionais quanto acadêmicos. Acreditamos que regressão linear é o conteúdo mais importante (logo atrás de \(p\)-valores) desse conjunto de tutoriais. Tal importância se dá por dois fatores. Primeiro, todas as técnicas estatística que vimos até agora (teste \(t\), ANOVA e correlação) podem ser substituídas por casos especiais de regressão linear. Segundo, eles são a base de entendimento para todos os modelos de regressão existentes (alguns listados na seção de “Técnicas Avançadas”).

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Big Sur 11.4

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1-arm64/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] gt_0.3.0         lm.beta_1.5-1    car_3.0-11      
 [4] carData_3.0-4    lmtest_0.9-38    zoo_1.8-9       
 [7] ggfortify_0.4.11 sjPlot_2.8.8     skimr_2.1.3     
[10] cowplot_1.1.1    broom_0.7.8      patchwork_1.1.1 
[13] dplyr_1.0.7      ggplot2_3.3.5   

loaded via a namespace (and not attached):
 [1] nlme_3.1-152       insight_0.14.2     RColorBrewer_1.1-2
 [4] repr_1.1.3         tools_4.1.0        backports_1.2.1   
 [7] bslib_0.2.5.1      utf8_1.2.1         R6_2.5.0          
[10] sjlabelled_1.1.8   DBI_1.1.1          mgcv_1.8-35       
[13] colorspace_2.0-2   withr_2.4.2        tidyselect_1.1.1  
[16] gridExtra_2.3      emmeans_1.6.1      downlit_0.2.1     
[19] curl_4.3.2         compiler_4.1.0     performance_0.7.2 
[22] textshaping_0.3.5  labeling_0.4.2     bayestestR_0.10.0 
[25] sass_0.4.0         checkmate_2.0.0    scales_1.1.1      
[28] mvtnorm_1.1-2      commonmark_1.7     systemfonts_1.0.2 
[31] stringr_1.4.0      digest_0.6.27      foreign_0.8-81    
[34] minqa_1.2.4        rmarkdown_2.9      rio_0.5.27        
[37] base64enc_0.1-3    pkgconfig_2.0.3    htmltools_0.5.1.1 
[40] lme4_1.1-27.1      highr_0.9          readxl_1.3.1      
[43] rlang_0.4.11       jquerylib_0.1.4    farver_2.1.0      
[46] generics_0.1.0     jsonlite_1.7.2     zip_2.2.0         
[49] distill_1.2        magrittr_2.0.1     parameters_0.14.0 
[52] Matrix_1.3-4       Rcpp_1.0.6         munsell_0.5.0     
[55] fansi_0.5.0        abind_1.4-5        lifecycle_1.0.0   
[58] stringi_1.6.2      yaml_2.2.1         snakecase_0.11.0  
[61] MASS_7.3-54        grid_4.1.0         forcats_0.5.1     
[64] sjmisc_2.8.7       crayon_1.4.1       lattice_0.20-44   
[67] haven_2.4.1        ggeffects_1.1.0    splines_4.1.0     
[70] hms_1.1.0          sjstats_0.18.1     magick_2.7.2      
[73] knitr_1.33         pillar_1.6.1       boot_1.3-28       
[76] estimability_1.3   effectsize_0.4.5   glue_1.4.2        
[79] evaluate_0.14      data.table_1.14.0  modelr_0.1.8      
[82] vctrs_0.3.8        nloptr_1.2.2.2     cellranger_1.1.0  
[85] gtable_0.3.0       purrr_0.3.4        tidyr_1.1.3       
[88] assertthat_0.2.1   openxlsx_4.2.4     xfun_0.24         
[91] xtable_1.8-4       coda_0.19-4        ragg_1.1.3        
[94] tibble_3.1.2       ellipsis_0.3.2    

---

1. variáveis dependentes binárias ou discretas serão apresentadas na tutorial de Regressão Logística↩︎

2. regressão também é o motor que tem por de trás de quase todos os algoritmos e modelos de machine learning.↩︎

3. tecnicamente reta aqui se refere um hiperplano que é subespaço de dimensão \(n-1\) de um espaço de dimensão \(n\). Por exemplo, uma reta é um hiperplano 1-D de uma plano 2-D; um plano 2-D é um hiperplano de um plano 3-D; e assim por diante…↩︎

4. acreditamos que visualizações 3-D de dados somente são aplicáveis em dois contextos: se você está usando mapas nas suas visualizações ou se você possui uma impressora 3D. Como não estamos fazendo nenhum dos dois, não nos aventuraremos em imagens 3D (#ficaadica).↩︎

5. usando a técnica de Pearson.↩︎

6. tecnicamente podemos também pegar o valor absoluto de cada erro. Isto se chama erro absoluto médio (mean absolute error – MAE). Mas não possui as mesmas propriedades analíticas que o MSE e é computacionalmente menos estável.↩︎

7. Para os que tenham tido a oportunidade de estudar cálculo: estamos falando em achar o valor de x quando a derivada do MSE é zero (\(\text{MSE}^{\prime} = 0\)).↩︎

8. usando a técnica de Pearson.↩︎

9. convertemos cyl em fator para que, no gráfico cyl seja representado como quantidades discretas ao invés de contínuas.↩︎

10. matematicamente falando interação é uma multiplicação entre as duas variáveis independentes↩︎

11. muitas definições usam o termo “explicada” o que evitamos pois implica intuitivamente em uma relação causal.↩︎

12. inclusive a função aov() de ANOVA por de baixo dos panos faz um chamado à função lm(). Ou seja é um wrapper, também chamado de açúcar sintático (syntactic sugar), da função lm().↩︎

13. Termo inglês: M-estimation↩︎

14. Termo inglês: least trimmed squares – LTS↩︎