Regressão Logística

Regressão para o caso de uma variável dependente binária.

A regressão linear é uma técnica tão ampla que originou diversas gambiarras extensões para acomodar os mais diferentes tipos de variáveis dependentes para além de apenas contínuas. Essas extensões da regressão linear são chamadas de modelos lineares generalizados e a sua lógica se baseia em transformar a variável dependente de alguma maneira para que ela se torne “linear” e “contínua”. Nesse tutorial vamos focar no caso da regressão logística que usa uma transformação logística de variáveis binárias (também chamadas de dicotômicas ou dummy) – que tomam apenas dois valores discretos¹. Antes de continuar, recomendamos fortemente que leia o tutorial nosso de regressão linear, pois muitos conceitos serão abordados novamente.

O foco em variáveis binárias (logo, em regressão logística) se dá pela quantidade de dados e modelos que são usados para modelar resultados binários. Por exemplo:

• Como a probabilidade de desenvolver câncer de pulmão (sim vs. não) muda para cada quilo adicional que uma pessoa está acima do peso e para cada maço de cigarros fumado por dia?
• O peso corporal, a ingestão de calorias, a ingestão de gordura e a idade influenciam a probabilidade de um ataque cardíaco (sim x não)?
• Quais palavras, qual hora do dia, quais assuntos e qual domínio do remetentem influenciam a probabilidade de um e-mail ser spam (sim x não)?

Todos esses exemplos são questões que a regressão logística pode responder. Toda vez que precisamos responder uma pergunta na qual pode ser reduzida a uma pergunta de sim/não ou esse/aquele, regressão logística é a principal técnica a ser empregada.

Função Logística

Uma regressão logística se comporta exatamente como um modelo linear: faz uma predição simplesmente computando uma soma ponderada das variáveis independentes, mais uma constante. Porém ao invés de retornar um valor contínuo, como a regressão linear, retorna a função logística desse valor.

\[\operatorname{Logística}(x) = \frac{1}{1 + e^{(-x)}}\]

A função logística é uma gambiarra transformação que pega qualquer valor entre menos infinito \(-\infty\) e mais infinito \(+\infty\) e transforma em um valor entre 0 e 1. Veja na figura 1 uma representação gráfica da função logística.

library(dplyr)
library(ggplot2)
tibble(
  x = seq(-10, 10, length.out = 100),
  logit = 1 / (1 + exp(-x))) %>%
  ggplot(aes(x, logit)) +
  geom_line()

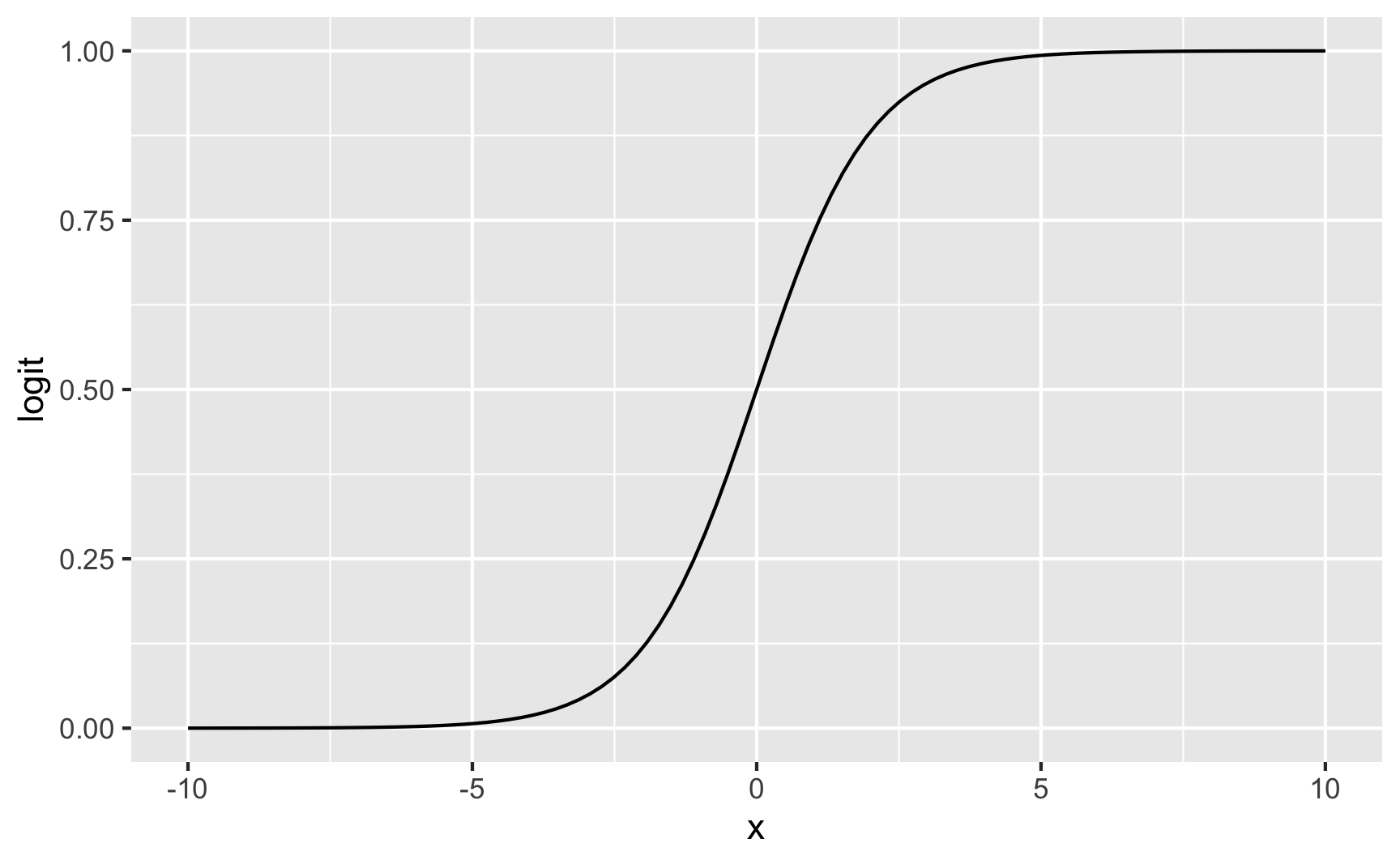
Figure 1: Função Logística

A função logística foi desenvolvida como modelo de crescimento populacional e denominada “logística” por Pierre François Verhulst nas décadas de 1830 e 1840, sob a orientação de Adolphe Quetelet. Regressão Logística como a empregamos hoje passou por vários refinamentos até Cox (1958) que é mais ou menos a versão atual que usamos.

Figure 2: Da esquerda para direita: Pierre François Verhuls, Adolphe Quetelet e David Cox – Figuras de https://www.wikipedia.org

Por que não usar Regressão Linear?

Para responder essa pergunta recorreremos mais uma vez à simulações. Vamos gerar um dataset com 30 observações com duas variáveis: uma variável contínua idade e uma variável binária comprado. Para ilustrar o primeiro cenário, imagine que somente as pessoas com menos de 20 anos compraram algum produto, comprado = 1, e as pessoas com 20 anos ou mais não compraram o produto, comprado = 0. Veja na figura 3 o que acontece se usarmos uma regressão linear (em vermelho) ou uma regressão logística (em azul) neste cenário. Qual modelo explica melhor a relação entre os dados é evidente: regressão logística.

sim1 <- tibble(
  idade = 10:29,
  comprado = c(rep(1, 10), rep(0, 10))
)

sim1 %>% ggplot(aes(idade, comprado)) +
  geom_point() +
  geom_smooth(method = "lm", se =  FALSE, color = "Red") +
  geom_smooth(method = "glm",
              method.args = list(family = "binomial"),
              se = FALSE, color = "Blue") +
  scale_y_continuous(breaks = c(0, 1))

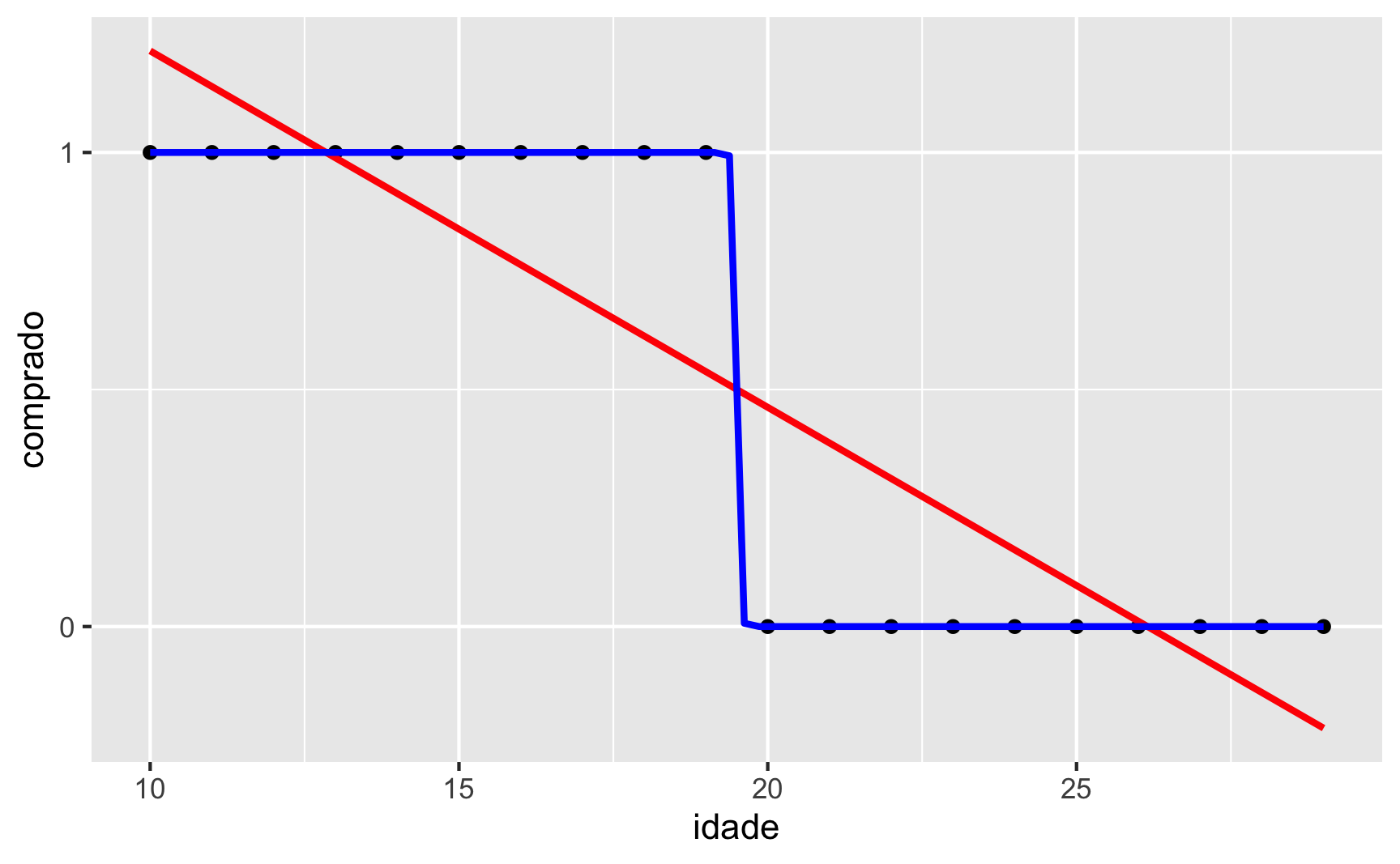
Figure 3: Reta vs Curva Logística

Vamos para uma segunda simulação, agora com dados desbalanceados. Vamos adicionar à nossa simulação mais 10 clientes com idades entre 60 e 69 que não comparam o produto comprado = 0. Nesse cenário, figura 4, a desvantagem da regressão linear (cor vermelha) comparada com a regressão logística (cor azul) é ainda mais evidente.

sim2 <- tibble(
  idade = c(10:29, 60:69),
  comprado = c(rep(1, 10), rep(0, 20))
)

sim2 %>% ggplot(aes(idade, comprado)) +
  geom_point() +
  geom_smooth(method = "lm", se =  FALSE, color = "Red") +
  geom_smooth(method = "glm",
              method.args = list(family = "binomial"),
              se= FALSE, color = "Blue") +
  scale_y_continuous(breaks = c(0, 1))

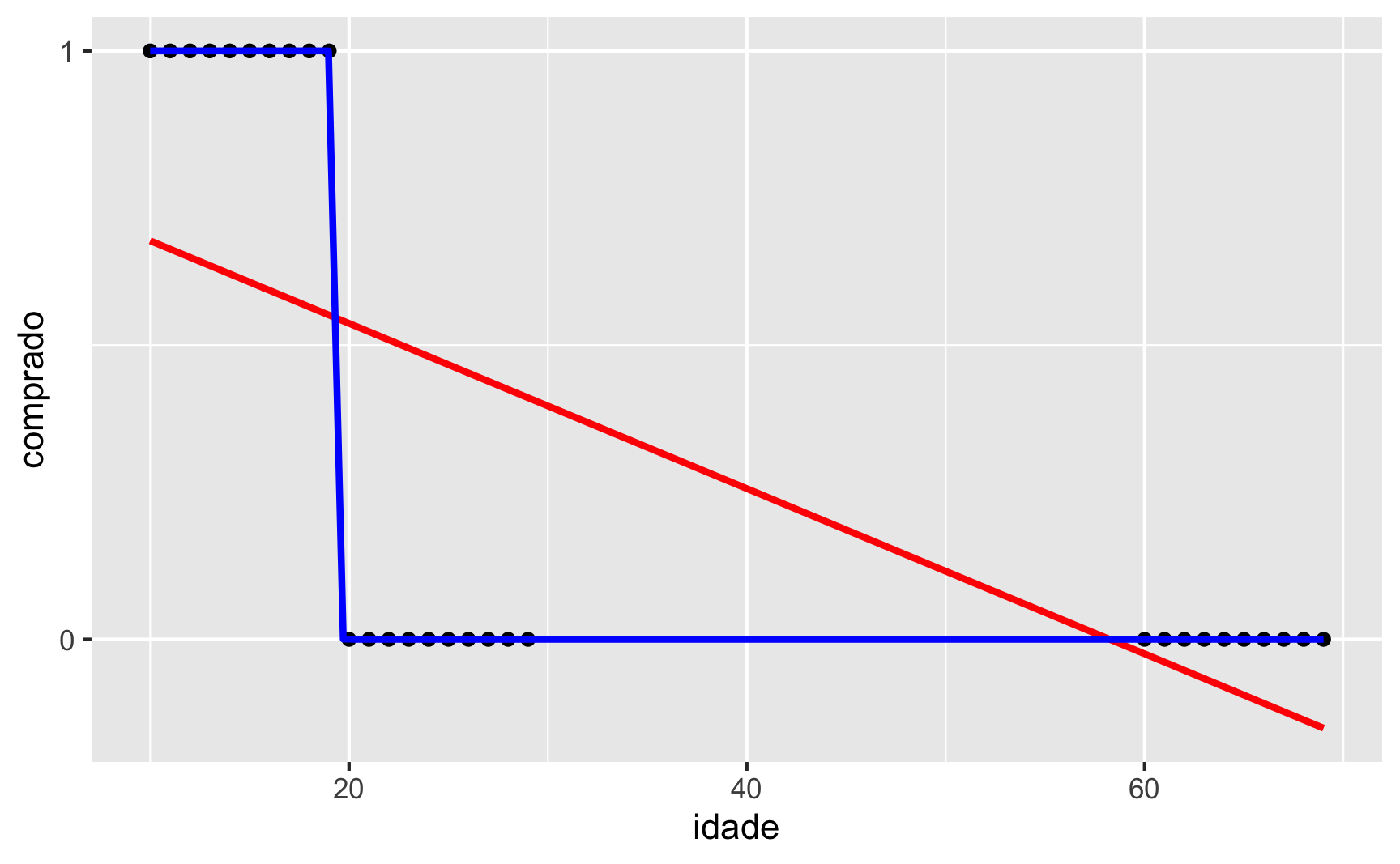
Figure 4: Reta vs Curva Logística – Dados Desbalanceados

Acreditamos que com essas duas simulações o argumento a favor de regressão logística tenha sido aceito incondicionalmente.

Pressupostos da Regressão Logística

Para interpretar os resultados de uma regressão logística como uma quantidade estatística significativa que mede os relacionamentos do mundo real, precisamos contar com uma série de suposições clássicas. Os quatro principais pressupostos da regressão logística são:

1. Independência dos Dados: o valor de uma observação não influencia ou afeta o valor de outras observações. Este é o pressuposto clássico de todas as técnicas abordadas até agora.
2. Linearidade dos Dados: a relação entre as variáveis independentes e a curva logística da variável dependente é considerada linear (quanto mais/menos de uma, mais/menos de outra). Linearidade dos Dados pode ser verificada graficamente observando a dispersão dos resíduos com os valores previstos pela regressão.
3. Independência dos Erros / Resíduos: os erros (também chamados de resíduos) não devem possuir correlação. Este pressuposto pode ser testado pelo teste de Durbin-Watson e observando o gráfico quantil-quantil (Q-Q) dos resíduos padronizados.
4. Homogeneidade de Variância dos Erros / Resíduos: os erros devem ter média zero e desvio padrão constante ao longo das observações. Similar ao teste de Levene, mas aplicado aos resíduos da regressão. Pode ser testado usando o Teste de Breusch-Pagan.
5. Ausência de Multicolinearidade: multicolinearidade é a ocorrência de alta correlação entre duas ou mais variáveis independentes e pode levar a resultados distorcidos. Em geral, a multicolinearidade pode fazer com que os intervalos de confiança se ampliem, ou até mudar o sinal de influência das variáveis independentes (de positivo para negativo, por exemplo). Portanto, as inferências estatísticas de uma regressão com multicolinearidade não são confiáveis. Pode ser testado usando o Fator de Inflação de Variância (Variance Inflation Factor – VIF).

Os pressupostos de regressão logística são os mesmos da regressão linear, com a exceção de que o pressuposto de linearidade é aplicado à curva logística da variável dependente.

Como aplicar uma Regressão Logística no R

Para exemplificar as regressões nesse tutorial, usaremos o dataset TitanicSurvival da biblioteca {carData} (Fox & Weisberg, 2019). TitanicSurvival é uma base de dados com os tripulantes e passageiros do Titanic que afundou em 15 de Abril de 1912. Possui 1309 observações e 4 variáveis:

• survived – sobreviveu (binária qualitativa): 0 não sobreviveu, 1 sobreviveu
• sex – gênero (binária qualitativa): female feminino, male masculino
• age – idade (contínua)
• passengerClass – classe do passageiro (qualitativa): 1st primeira classe, 2nd segunda classe e 3rd terceira classe

library(skimr)
library(carData)
data("TitanicSurvival", package = "carData")
skim(TitanicSurvival)

Table 1: Data summary

Name	TitanicSurvival
Number of rows	1309
Number of columns	4
_______________________
Column type frequency:
factor	3
numeric	1
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
survived	0	1	FALSE	2	no: 809, yes: 500
sex	0	1	FALSE	2	mal: 843, fem: 466
passengerClass	0	1	FALSE	3	3rd: 709, 1st: 323, 2nd: 277

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
age	263	0.8	29.88	14.41	0.17	21	28	39	80	▂▇▅▂▁

Para aplicar uma regressão logística no R usamos a função glm() (generalized linear model) padrão do R. Sua funcionalidade é idêntica à função lm() de regressão linear, sendo que, além de fórmula e dataset, é necessário fornecer um argumento extra family:

1. Fórmula designando a variável dependente e a(s) variável(eis) independente(s) designada pela seguinte síntaxe: dependente ~ independente_1 + independente_2 + ....
2. O dataset no qual deverá ser encontradas as variáveis presentes na fórmula.
3. family: tipo de modelo linear generalizado que deseja utilizar. Para regressão logística usamos family = binomial.

Começaremos com um exemplo simples de regressão logística do TitanicSurvival usando como variável independente survived e variáveis independentes age e sex. Podemos inspecionar o resultado de uma regressão logística com a função summary().

modelo_simples <- glm(survived ~ age + sex,
                      data = TitanicSurvival, family = binomial)
summary(modelo_simples)

Call:
glm(formula = survived ~ age + sex, family = binomial, data = TitanicSurvival)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.7247  -0.6859  -0.6603   0.7555   1.8737  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  1.235414   0.192032   6.433 1.25e-10 ***
age         -0.004254   0.005207  -0.817    0.414    
sexmale     -2.460689   0.152315 -16.155  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1414.6  on 1045  degrees of freedom
Residual deviance: 1101.3  on 1043  degrees of freedom
  (263 observations deleted due to missingness)
AIC: 1107.3

Number of Fisher Scoring iterations: 4

Interpretação dos Coeficientes

Na saída de summary() podemos ver que são produzidos os coeficientes da regressão na coluna Estimate, associados ao respectivos desvio padrão dos resíduos Std. Error e \(p\)-valores Pr(>|t|). Importante destacar que a hipótese nula dos coeficientes da regressão é de que “os coeficientes são nulos/zeros”, então os \(p\)-valores devem ser interpretados como a probabilidade de observamos valores de coeficientes tão extremos dado que a hipótese nula é verdadeira. Para facilitar, o R informa com asteriscos quais variáveis possuem coeficientes estatisticamente significantes: * para \(p < 0.05\), ** para \(p < 0.01\), e *** para \(p < 0.001\).

Os coeficientes de regressão logística não são interpretáveis em escala bruta². É necessário inverter a transformação logística exponenciando os coeficientes – \(e^x\). Isso faz com que os coeficientes se transformem em razões de chance (odds ratio – OR) que permite uma melhor interpretabilidade.

Razões de chance funcionam muito similar com as chances de uma aposta. Quando a chance é justa tanto para a variável dependente ser 0 quanto 1 ela é expressada como uma chance 1 para 1 (1:1) – \(\frac{1}{1}\). Qualquer valor abaixo de 0 faz com que a chance da variável dependente ser 0 aumentar, e qualquer valor acima de 1 a chance da variável dependente ser 1 aumenta. Para transformar os coeficientes de um modelo de regressão logística em OR, usamos a função exp() base do R nos coeficientes coef() do modelo.

exp(coef(modelo_simples))

(Intercept)         age     sexmale 
 3.43980286  0.99575479  0.08537609 

A interpretação dessa saída de OR é a seguinte:

• age – A cada aumento de uma unidade de idade, há uma diminuição da chance de sobrevivência (variável dependente survived igual a 1) em 0.424521% (\(1 - \text{OR}_\text{age}\)).
• sexmale – A cada aumento de uma unidade de sexmal (ou seja sexomale é igual 1, em outras palavras sexo masculino), há uma diminuição da chance de sobrevivência (variável dependente survived igual a 1) em 91.4623909% (\(1 - \text{OR}_\text{sexmale}\)).

Para produzir intervalos de confiança precisamos usar a função confint() do pacote MASS (Venables & Ripley, 2002), uma vez que a função confint() base do R não dá suporte à OR. Como padrão, MASS::confint(), assim como confint() base do R, produz intervalos de confiança 95%.

confint(modelo_simples)

                  2.5 %      97.5 %
(Intercept)  0.86469239  1.61820670
age         -0.01450821  0.00592225
sexmale     -2.76348286 -2.16607599

Variáveis Qualitativas

Além de variáveis independentes quantitativas, regressão logística, assim como a linear, também permite utilizarmos variáveis qualitativas (discretas) como variáveis independentes.

Vamos estender o nosso modelo simples adicionando a variável passengerClass. Note que, no dataset TitanicSurvival, passengerClass já está convertida para qualitativa (factor), não sendo necessário usar a função padrão do R as.factor().

modelo_quali <- glm(survived ~ age + sex + passengerClass,
                    data = TitanicSurvival, family = binomial)
summary(modelo_quali)

Call:
glm(formula = survived ~ age + sex + passengerClass, family = binomial, 
    data = TitanicSurvival)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.6399  -0.6979  -0.4336   0.6688   2.3964  

Coefficients:
                   Estimate Std. Error z value Pr(>|z|)    
(Intercept)        3.522074   0.326702  10.781  < 2e-16 ***
age               -0.034393   0.006331  -5.433 5.56e-08 ***
sexmale           -2.497845   0.166037 -15.044  < 2e-16 ***
passengerClass2nd -1.280570   0.225538  -5.678 1.36e-08 ***
passengerClass3rd -2.289661   0.225802 -10.140  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1414.62  on 1045  degrees of freedom
Residual deviance:  982.45  on 1041  degrees of freedom
  (263 observations deleted due to missingness)
AIC: 992.45

Number of Fisher Scoring iterations: 4

Quando uma variável é convertida para fator, o R rotula os diferentes níveis (levels) conforme ordem alfabética. Portanto, no nosso exemplo, passengerClass possui 3 níveis: 1st, 2nd e 3rd (apesar de serem números, na conversão o R usa uma ordem crescente para dígitos). Numa regressão logística que possua variáveis qualitativas codificadas como fatores, o R usará o primeiro nível do fator (no nosso caso 1st) como referência. Portanto a interpretações de passengerClass devem se atentar que a referência é passengerClass = 1st. É possível verificar os diferentes níveis das variáveis qualitativas de um objeto glm acessando seu atributo xlevels.

modelo_quali$xlevels

$sex
[1] "female" "male"  

$passengerClass
[1] "1st" "2nd" "3rd"

Efeitos Principais e Efeitos de Interação

Todos os modelos de regressão logística que mostramos até aqui usaram apenas efeitos principais. Mas podemos também mostrar efeitos de interação (também chamados de efeitos de moderação) entre duas variáveis. Similar ao exposto no tutorial sobre regressão linear, podemos incluir dois tipos de efeitos na regressão logística:

• Efeitos principais: efeito de uma (ou mais) variável(is) independente(s) em uma variável dependente. Chamamos esses efeitos de aditivos pois podem ser quebrados em dois efeitos distintos e únicos que estão influenciando a variável dependente.
• Efeitos de interações: quando o efeito de uma (ou mais) variável(is) independente(s) em uma variável dependente é afetado pelo nível de outras variável(is) independente(s). Efeitos de interação não são aditivos pois podem ser quebrados em dois efeitos distintos e únicos que estão influenciando a variável dependente. Há uma interação entre as variáveis independentes.

Veja na figura 5 uma representação gráfica da interação entre sex e passengerClass. Note que a interação é observada pela diferença de inclinações entre as linhas coloridas que representam os diferentes valores de passengerClass.

TitanicSurvival %>%
  mutate(survived = ifelse(survived == "yes", 1, 0),
         sex = forcats::fct_rev(sex)) %>%
  group_by(sex, passengerClass) %>%
  summarise(survived = mean(survived)) %>%
  ggplot(aes(x = sex, y = survived, color = passengerClass)) +
  geom_line(aes(group = passengerClass)) +
  geom_point() +
  scale_colour_brewer(palette = "Set1")

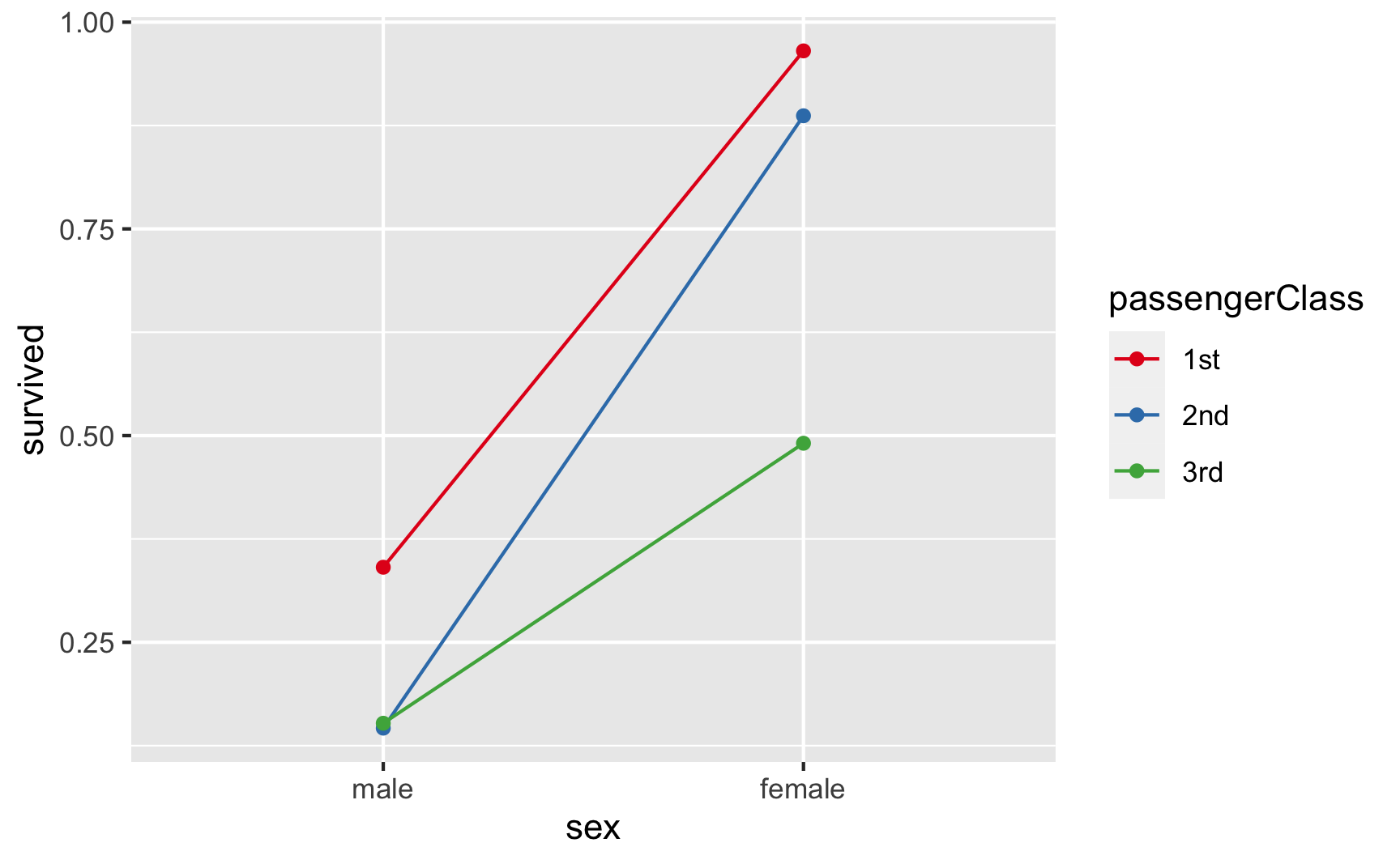
Figure 5: Interação entre sex e passengerClass do dataset mtcars

Para incluirmos efeitos de interações entre duas variáveis independentes em regressões logísticas, incluímos na fórmula entre as duas variáveis um sinal de multiplicação³ * indicando que as duas variáveis devem ser usadas como efeitos principais e também de interação na análise.

modelo_interacao <- glm(survived ~ age + sex * passengerClass,
                        data = TitanicSurvival, family = binomial)
summary(modelo_interacao)

Call:
glm(formula = survived ~ age + sex * passengerClass, family = binomial, 
    data = TitanicSurvival)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.0778  -0.6604  -0.4943   0.4263   2.4935  

Coefficients:
                           Estimate Std. Error z value Pr(>|z|)    
(Intercept)                4.804345   0.546937   8.784  < 2e-16 ***
age                       -0.038401   0.006743  -5.695 1.23e-08 ***
sexmale                   -3.886389   0.492375  -7.893 2.95e-15 ***
passengerClass2nd         -1.529875   0.566481  -2.701  0.00692 ** 
passengerClass3rd         -4.064965   0.510661  -7.960 1.72e-15 ***
sexmale:passengerClass2nd -0.070404   0.630978  -0.112  0.91116    
sexmale:passengerClass3rd  2.488808   0.540042   4.609 4.05e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1414.62  on 1045  degrees of freedom
Residual deviance:  931.99  on 1039  degrees of freedom
  (263 observations deleted due to missingness)
AIC: 945.99

Number of Fisher Scoring iterations: 5

A interpretação de interações de regressão logística é a mesma da interpretação de interações da regressão linear. Por exemplo, a interpretação do coeficiente sexmale:passengerClass3rd é a seguinte: ser um passageiros da terceira classe modera positivamente a relação entre sexo masculino e survived. Note que o \(p\)-valor de sexmale:passengerClass3rd possui significância estatística (\(p < 0.001\)).

Visualização de Regressão Logística

Uma vez que as variáveis dos modelos de regressão começam a ficar numerosas, as visualizações podem ajudar. Em especial, gostamos bastante da biblioteca {sjPlot} (Lüdecke, 2020) e sua função plot_model(). Como padrão, a função plot_model() produz um gráfico de floresta (forest plot) e também conhecido como blobograma no qual podemos visualizar as variáveis no eixo vertical e o tamanho do efeito, os coeficientes, no eixo horizontal. Além disso, coeficientes positivos são representados com a cor azul e negativos em vermelho; e os intervalos de confiança 95% como uma linha ao redor do valor médio do coeficiente (ponto). Ao especificarmos o tipo como "std" em plot_model(), o gráfico de floresta produzido utiliza os valores padronizados em desvios padrões. Já mostramos a função plot_model() no tutorial de regressão linear e ela funciona de maneira idêntica à modelos de regressão logística, com uma exceção que os coeficientes já são apresentados em formato OR. Veja um exemplo na figura 6: na parte superior temos o gráfico de floresta para coeficientes brutos e na parte inferior para coeficientes padrões.

library(sjPlot)
forest_raw <- plot_model(modelo_quali)
forest_std <- plot_model(modelo_quali, type = "std")
forest_raw + forest_std + plot_layout(nrow = 2, widths = 1)

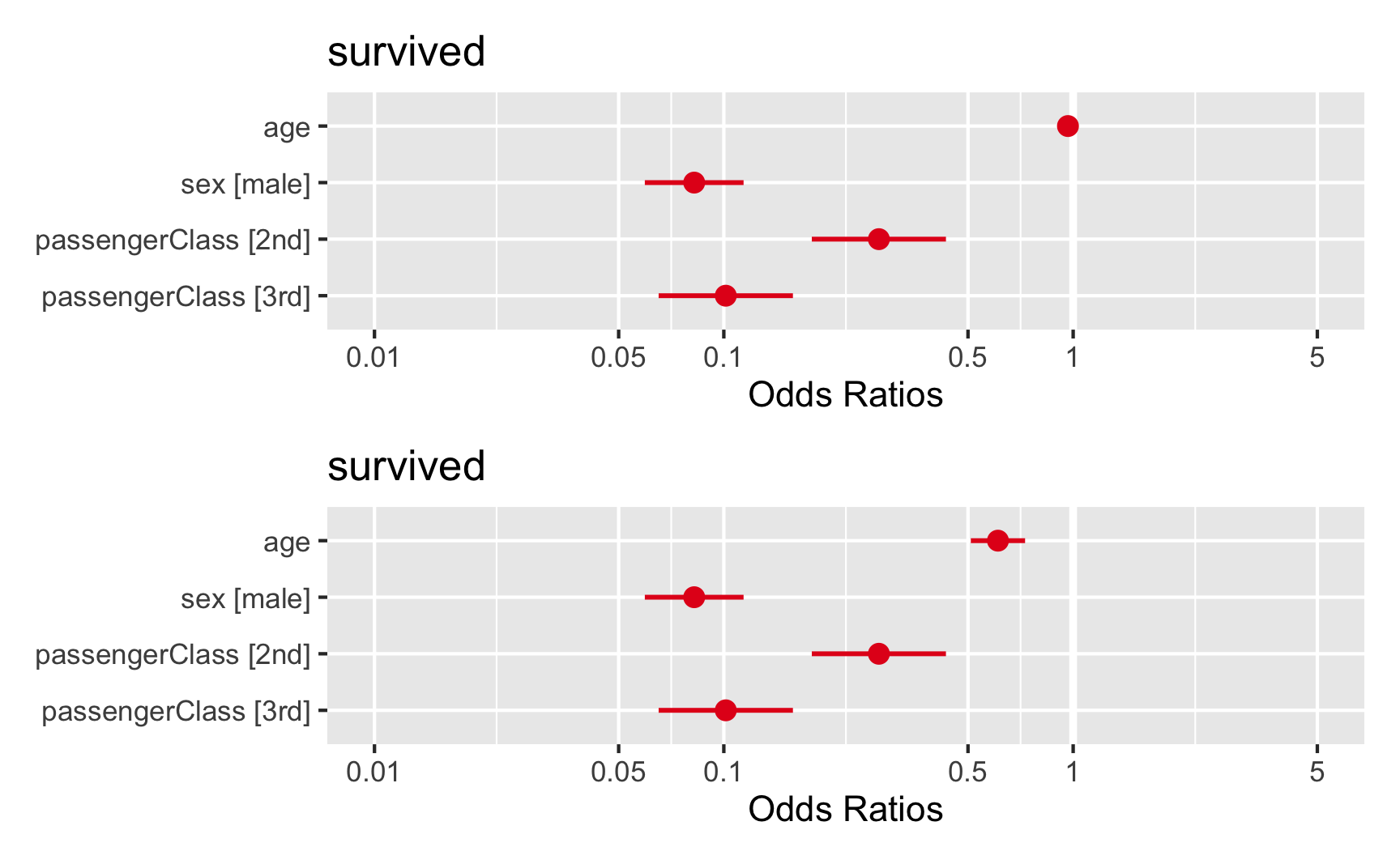
Figure 6: Gráfico de Floresta dos Coeficientes de uma Regressão Logística em formato Odds Ratio – OR

Caso queira mais opções de visualizações para modelos de regressão não deixe de conferir o site da biblioteca {sfPlot}.

Verificação de Pressupostos

Podemos realizar diversos testes estatísticos de hipótese nula para verificar se o modelo de regressão logística possui pressupostos violados ou não. Para isso recomendamos a biblioteca {lmtest} (Zeileis & Hothorn, 2002).

Os pressupostos de regressão logística são os mesmos da regressão linear, com a exceção de que o pressuposto de linearidade é aplicado à curva logística da variável dependente.

Teste de Breusch-Pagan

O teste de Breusch-Pagan(Breusch & Pagan, 1979; Cook & Weisberg, 1983) usado para testar o pressuposto da independência dos resíduos possui como hipótese nula que “as variâncias de erro são todas iguais” e como hipótese alternativa que “as variâncias de erro são uma função multiplicativa de uma ou mais variáveis.” Recomendamos que usem os resíduos “Studentizados” (quociente resultante da divisão de um resíduo por uma estimativa de seu desvio padrão – uma forma de estatística \(t\) de Student, com a estimativa de erro variando entre os pontos) no teste de Breusch-Pagan (Koenker, 1981). A função bptest() da biblioteca {lmtest} aceita como argumento um modelo de regressão logística (objeto glm) e já possui como padrão resíduos “Studentizados.” Caso queira usar resíduos brutos indique o argumento studentize como FALSE.

library(lmtest)
bptest(modelo_simples)

    studentized Breusch-Pagan test

data:  modelo_simples
BP = 19.793, df = 2, p-value = 5.035e-05

Note que o \(p\)-valor do Teste de Breusch-Pagan para o modelo_simples é menor que 0.05, demonstrando fortes evidências em favor da não rejeição da hipótese nula de dependência dos resíduos.

Teste de Durbin-Watson

O teste de Durbin-Watson (Durbin & Watson, 1950, 1951) é um teste estatístico usado para detectar a presença de autocorrelação dos resíduos de um modelo de regressão e testa o pressuposto da homogeneidade de variância dos resíduos. Possui como hipótese nula que os “erros são serialmente não correlacionados.” A função dwtest() da biblioteca {lmtest} aceita como argumento um modelo de regressão logística (objeto glm).

dwtest(modelo_simples)

    Durbin-Watson test

data:  modelo_simples
DW = 1.7134, p-value = 1.678e-06
alternative hypothesis: true autocorrelation is greater than 0

Note que o \(p\)-valor do Teste de Durbin-Watson para o modelo_simples é menor que 0.05, indicando a rejeição da hipótese nula de não-correlação, violando o pressuposto da homogeneidade de variância dos resíduos.

Multicolinearidade

Multicolinearidade é a ocorrência de alta correlação entre duas ou mais variáveis independentes e pode levar a resultados distorcidos. Em geral, a multicolinearidade pode fazer com que os intervalos de confiança se ampliem, ou até mudar o sinal de influência das variáveis independentes (de positivo para negativo, por exemplo). Portanto, as inferências estatísticas de uma regressão com multicolinearidade não são confiáveis. Pode ser testado usando o Fator de Inflação de Variância (Variance Inflation Factor – VIF).

Os VIFs medem o quanto da variância de cada coeficiente de regressão do modelo estatístico se encontra inflado em relação à situação em que as variáveis independentes não estão correlacionadas. Valores aceitáveis de VIF são menores que 10 (Hair et al., 1998). Para calcular os VIFs de uma modelo de regressão logística glm use a função vif() da biblioteca {car} (Fox & Weisberg, 2019).

library(car)
vif(modelo_simples)

     age      sex 
1.001022 1.001022 

Note que os valores de VIFs para as variáveis independentes do modelo_simples estão todos dentro do limite aceitável (\(<10\)), demonstrando ausência de multicolinearidade e evidenciando que o pressuposto não foi violado.

Pseudo-\(R^2\)

Observe que, embora muitos softwares estatísticos computem um pseudo-\(R^2\) para modelos de regressão logística, essa medida de determinação não é diretamente comparável ao \(R^2\) calculado para modelos de regressão linear. Na verdade, alguns estatísticos recomendam evitar a publicação de \(R^2\) (Harrell Jr, 2015; Hosmer Jr, Lemeshow, & Sturdivant, 2013), uma vez que pode ser mal interpretado em um contexto de regressão logística.

Há várias técnicas de como calcular um pseudo-\(R^2\) propostas na literatura sendo que a principal é o pseudo-\(R^2\) e pseudo-\(R^2\) ajustado de McFadden (McFadden & others, 1973).

A função PseudoR2() da biblioteca {DescTools} (Andri et mult. al., 2020) possui todas as principais técnicas de cálculo de pseudo-\(R^2\) podendo ser especificadas com o argumento which⁴.

library(DescTools)
PseudoR2(modelo_simples, which = c("McFadden", "McFaddenAdj"))

   McFadden McFaddenAdj 
  0.2214598   0.2172183 

Técnicas Avançadas de Modelos Lineares Generalizados.

Assim como no tutorial de Regressão Linear, nesta seção apenas apresentaremos alternativas avançadas, não é o foco desse conteúdo introdutório apresentar de maneira detalhada, mas sim de apontar o leitor na direção correta.⁵

• Modelos Lineares Generalizados Regularizados
• Modelos Aditivos Generalizados
• Modelos Lineares Generalizados Multiníveis

Modelos Lineares Generalizados Regularizados

Modelos lineares generalizados regularizados são um tipo de modelos lineares generalizados em que as estimativas dos coeficientes são restritas a zero. A magnitude (tamanho) dos coeficientes, bem como a magnitude do termo de erro, são penalizados. Modelos complexos são desencorajados, principalmente para evitar overfitting.

Tipos de Modelos Lineares Generalizados Regularizados

Dois tipos comumente usados de métodos de modelos lineares generalizados regularizados são Ridge e Lasso.

Ridge(Tikhonov, 1943) é uma forma de criar um modelo parcimonioso quando o número de variáveis preditoras em um conjunto excede o número de observações (\(m > p\)) ou quando um conjunto de dados tem forte multicolinearidade (correlações entre variáveis preditoras). A regressão Ridge pertence ao conjunto de ferramentas de regularização L2. A regularização L2 adiciona uma penalidade chamada penalidade L2, que é igual ao quadrado da magnitude dos coeficientes. Todos os coeficientes são reduzidos pelo mesmo fator, de modo que todos os coeficientes permanecem no modelo. A força do termo de penalidade é controlada por um parâmetro de ajuste. Quando este parâmetro de ajuste (\(\lambda\)) é definido como zero, a regressão Ridge é igual à um modelo linear generalizado. Se \(\lambda = \infty\), todos os coeficientes são reduzidos a zero. A penalidade ideal é, portanto, algo entre \(0\) e \(\infty\).

Lasso (least absolute shrinkage and selection operator – Lasso) (Efron & Hastie, 2016; Tibshirani, 1996) é um tipo de modelo linear generalizado que usa encolhimento (shrinkage). Encolhimento faz com os valores dos coeficientes sejam reduzidos em direção a um ponto central, como a média. Este tipo de redução é muito útil quando você tem altos níveis de muticolinearidade ou quando deseja automatizar certas partes da seleção de modelo, como seleção de variável / eliminação de parâmetro. Lasso usa a regularização L1 que limita o tamanho dos coeficientes adicionando uma penalidade L1 igual ao valor absoluto, ao invés do valor quadrado como L2, da magnitude dos coeficientes. Isso às vezes resulta na eliminação de alguns coeficientes completamente, o que pode resultar em modelos esparsos e seleção de variáveis.

Para usar modelos lineares generalizados regularizados use a biblioteca {glmnet} (Simon, Friedman, Hastie, & Tibshirani, 2011).

Regressão Aditiva - Modelos Aditivos Generalizados

Em estatística, um modelo aditivo generalizado (generalized additive model – GAM) é um modelo linear generalizado no qual a variável de resposta depende linearmente de funções suaves (chamadas de splines) desconhecidas de algumas variáveis preditoras, e o interesse se concentra na inferência sobre essas funções suaves. Os GAMs foram desenvolvidos originalmente por Trevor Hastie e Robert Tibshirani (Hastie, Tibshirani, & others, 1986). Para usar GAMs no R use a biblioteca {gam} (Hastie, 2020).

Regressão Multinível

Modelos multiníveis (também conhecidos como modelos lineares hierárquicos, modelo linear de efeitos mistos, modelos mistos, modelos de dados aninhados, coeficiente aleatório, modelos de efeitos aleatórios, modelos de parâmetros aleatórios ou designs de gráfico dividido) são modelos estatísticos de parâmetros que variam em mais de um nível (Luke, 2019).

Modelos multiníveis são particularmente apropriados para projetos de pesquisa onde os dados dos participantes são organizados em mais de um nível (ou seja, dados aninhados). As unidades de análise geralmente são indivíduos (em um nível inferior) que estão aninhados em unidades contextuais / agregadas (em um nível superior).

Modelos multiníveis geralmente se dividem em três abordagens:

1. Random intercept model: Modelo no qual cada grupo recebe uma constante (intercept) diferente
2. Random slope model: Modelo no qual cada grupo recebe um coeficiente diferente para cada variável independente
3. Random intercept-slope model: Modelo no qual cada grupo recebe tanto uma constante (intercept) quanto um coeficiente diferente para cada variável independente

O primeiro autor possui um tutorial de Estatística Bayesiana com R e uma dos tutoriais é sobre regressão multinível.

Para usar modelos multiníveis em R use a biblioteca {lme4} (Bates, Mächler, Bolker, & Walker, 2015).

Comentários Finais

Regressão logística é a principal técnica de modelos lineares generalizados – extensão da regressão linear, sendo usada amplamente tanto em relatórios técnicos quanto na literatura científica, assim como tanto em contextos profissionais quanto acadêmicos. Caso o leitor tenha se interessado, convidamos à conhecer as outras técnicas de modelos lineares generalizados (Nelder & Wedderburn, 1972), como regressão de Poisson, regressão Binomial negativa, entre outros…

Ambiente

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] gt_0.2.2             lm.beta_1.5-1        lmtest_0.9-38       
 [4] zoo_1.8-8            ggfortify_0.4.11     sjPlot_2.8.7        
 [7] broom_0.7.4          palmerpenguins_0.1.0 magrittr_2.0.1      
[10] mnormt_2.0.2         cowplot_1.1.1        tidyr_1.1.2         
[13] DescTools_0.99.40    skimr_2.1.2          ggpubr_0.4.0        
[16] car_3.0-10           carData_3.0-4        patchwork_1.1.1     
[19] dplyr_1.0.4          ggplot2_3.3.3        DiagrammeR_1.0.6.1  
[22] readxl_1.3.1        

loaded via a namespace (and not attached):
  [1] minqa_1.2.4        colorspace_2.0-0   ggsignif_0.6.0    
  [4] ellipsis_0.3.1     class_7.3-17       rio_0.5.16        
  [7] sjlabelled_1.1.7   rprojroot_2.0.2    estimability_1.3  
 [10] parameters_0.11.0  base64enc_0.1-3    gld_2.6.2         
 [13] rstudioapi_0.13    farver_2.0.3       fansi_0.4.2       
 [16] mvtnorm_1.1-1      lubridate_1.7.9.2  xml2_1.3.2        
 [19] splines_4.0.3      downlit_0.2.1      rootSolve_1.8.2.1 
 [22] knitr_1.31         sjmisc_2.8.6       jsonlite_1.7.2    
 [25] nloptr_1.2.2.2     ggeffects_1.0.1    effectsize_0.4.3  
 [28] compiler_4.0.3     emmeans_1.5.4      sjstats_0.18.1    
 [31] backports_1.2.1    assertthat_0.2.1   Matrix_1.2-18     
 [34] cli_2.3.0          visNetwork_2.0.9   htmltools_0.5.1.1 
 [37] tools_4.0.3        gtable_0.3.0       glue_1.4.2        
 [40] lmom_2.8           Rcpp_1.0.6         cellranger_1.1.0  
 [43] vctrs_0.3.6        nlme_3.1-149       insight_0.12.0    
 [46] xfun_0.21          stringr_1.4.0      lme4_1.1-26       
 [49] openxlsx_4.2.3     lifecycle_0.2.0    statmod_1.4.35    
 [52] rstatix_0.6.0      MASS_7.3-53        scales_1.1.1      
 [55] hms_1.0.0          expm_0.999-6       RColorBrewer_1.1-2
 [58] yaml_2.2.1         curl_4.3           Exact_2.1         
 [61] gridExtra_2.3      reticulate_1.18    sass_0.3.1        
 [64] distill_1.2        stringi_1.5.3      highr_0.8         
 [67] bayestestR_0.8.2   checkmate_2.0.0    e1071_1.7-4       
 [70] boot_1.3-25        zip_2.1.1          repr_1.1.3        
 [73] commonmark_1.7     rlang_0.4.10       pkgconfig_2.0.3   
 [76] evaluate_0.14      lattice_0.20-41    purrr_0.3.4       
 [79] htmlwidgets_1.5.3  labeling_0.4.2     tidyselect_1.1.0  
 [82] ggsci_2.9          bookdown_0.21      R6_2.5.0          
 [85] magick_2.6.0       generics_0.1.0     DBI_1.1.1         
 [88] pillar_1.4.7       haven_2.3.1        foreign_0.8-80    
 [91] withr_2.4.1        mgcv_1.8-33        abind_1.4-5       
 [94] tibble_3.0.6       performance_0.7.0  modelr_0.1.8      
 [97] crayon_1.4.1       utf8_1.1.4         tmvnsim_1.0-2     
[100] rmarkdown_2.6      grid_4.0.3         data.table_1.13.6 
[103] forcats_0.5.1      digest_0.6.27      xtable_1.8-4      
[106] munsell_0.5.0     

---

1. caso o leitor se interesse existe diversas outras transformações que dão origens a diferentes modelos lineares generalizados, veja Nelder & Wedderburn (1972).↩︎

2. em sua escala bruta os coeficientes de uma regressão logística estão representados como o logaritmo da chance (log odds).↩︎

3. matematicamente falando interação é uma multiplicação entre as duas variáveis independentes↩︎

4. podem ser escolhidas dentre as técnicas: "McFadden", "McFaddenAdj", "CoxSnell", "Nagelkerke", "AldrichNelson", "VeallZimmermann", "Efron", "McKelveyZavoina", "Tjur"; ou todas "all".↩︎

5. Note que todas as técnicas avançadas listadas aqui são as mesmas listadas no tutorial de Regressão Linear apenas com a nomenclatura de “modelos lineares generalizados” ao invés de “regressão linear.”↩︎