Teste de Médias – ANOVA Paramétrica e Não-Paramétrica

Como comparar as diferenças de uma variável para mais de dois grupos.

O teste \(t\) verifica a diferença de média entre dois grupos. E se eu tenho mais de dois grupos? A resposta mais inocente seria realizar múltiplos testes \(t\) entre os diversos grupos e comparar o tamanho de efeito e \(p\)-valor dos testes. Porém essa abordagem possui uma falha: conforme aumenta o número de testes¹ a taxa de falsos positivos (erros tipo I) aumentam quase na mesma proporção.

A fórmula para determinar a nova taxa de erro para múltiplos testes \(t\) não é tão simples quanto multiplicar 5% pelo número de testes. No entanto, se você estiver fazendo apenas algumas comparações múltiplas, os resultados serão muito semelhantes se você fizer isso. Como tal, três testes \(t\) seriam 15% (na verdade, 14.3%) e assim por diante.

A taxa de erro para múltiplos testes de \(t\) é chamada de taxa de erro familiar² e é definida como:

a probabilidade máxima de que um procedimento consistindo de mais de uma comparação conclua incorretamente que pelo menos uma das diferenças observadas é significativamente diferente da hipótese nula.

Para controlar a taxa de erro familiar, temos um conjunto de técnicas chamada análise de variância, conhecida como Analysis of Variance (ANOVA). A ANOVA controla esses erros para que os falsos positivos (erros tipo I) permaneçam em 5% na comparação de média entre dois ou mais grupos. A ANOVA não irá dizer com precisão como que as médias dos grupos diferem, mas o seu resultado indica fortes evidências de que a diferença entre as médias dos grupos difere. Sua hipótese nula é que não há diferença entre as médias dos grupos. A ANOVA tradicional é uma técnica paramétrica (quando a variável dependente é distribuída conforme uma distribuição Normal), mas há também uma versão não-paramétrica (quando não temos pressupostos sobre de que distribuição probabilística a variável dependente é distribuída) chamada teste de Kruskal-Wallis.

Após analisar os resultados de uma ANOVA, é muito comum realizar uma comparação post-hoc usando um conjunto de técnicas comparativas de média entre grupos que controlam a taxa de erro familiar. A principal técnica paramétrica é o teste de Tukey e a principal técnica não-paramétrica é o teste de Dunn.

História da ANOVA

A ANOVA foi primeira proposta por Ronald Fisher³ em 1921 (R. Fisher, 1921) e foi incluída no seu livro de 1925 que popularizou as técnicas de Estatística inferencial (R. A. Fisher, 1925). A estatística que a ANOVA calcula para testar sua hipótese nula é chamada de Estatística F, em homenagem à Fisher. Em 1919 Fisher foi trabalhar em um instituto de pesquisa agrícola chamado Rothamsted Experimental Station na Inglaterra, onde ficou até 1933. Foi nesse instituto que Fisher, ao ter acesso a uma vasta quantidade de dados sobre dados de safra agrícola acumulados desde 1842, desenvolveu e fez as primeiras aplicações de ANOVA.

Figure 1: Ronald Fisher. Figura de https://www.wikipedia.org

Dataset ToothGrowth

Dessa vez não vamos simular dados, mas vamos usar um dataset que vem padrão com o R chamado ToothGrowth (Crampton, 1947), que examina os efeitos da vitamina C no crescimento dos dentes em porquinhos da índia. Cada animal foi atribuído a um de seis grupos de 10 sujeitos cada (\(n = 10\)) para um total de 60 cobaias ao todo (\(N = 60\)). As duas variáveis que foram manipuladas neste estudo foram o nível de dosagem de vitamina C dose (0.5, 1.0 ou 2.0 mg / dia) e o método de entrega da dosagem supp (suco de laranja OJ ou ácido absorvico VC). A variável dependente é o comprimento dos denteslen dos porquinhos da índia.

Nós, sempre que carregamos um dataset no R, temos o costume de usar a biblioteca {skimr} (Waring et al., 2020) para produzir um sumário dos dados.

library(skimr)
data("ToothGrowth")
ToothGrowth$dose <- as.factor(ToothGrowth$dose)
skim(ToothGrowth)

Table 1: Data summary

Name	ToothGrowth
Number of rows	60
Number of columns	3
_______________________
Column type frequency:
factor	2
numeric	1
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
supp	0	1	FALSE	2	OJ: 30, VC: 30
dose	0	1	FALSE	3	0.5: 20, 1: 20, 2: 20

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
len	0	1	18.81	7.65	4.2	13.07	19.25	25.27	33.9	▅▃▅▇▂

Além disso é interessante computar uma tabela de frequência com a função padrão do R table() das duas variáveis independentes supp e dose:

table(ToothGrowth$supp, ToothGrowth$dose)

    
     0.5  1  2
  OJ  10 10 10
  VC  10 10 10

ANOVA

A ANOVA é uma técnica paramétrica e seus pressupostos são similares ao teste \(t\) de Student:

• Independência das observações: o valor de uma observação não influencia ou afeta o valor de outras observações.
• Normalidade: variável dependente distribuída conforme uma distribuição Normal.
• Homogeneidade das Variâncias: variável dependente possui homogeneidade de variância dentre os grupos.

Além disso, a ANOVA é utilizada apenas quando as variáveis independentes são categóricas (discretas, como por exemplo grupos diferentes).

O pressuposto da normalidade, já coberto na tutorial de \(p\)-valores, pode ser testado com o teste de Shapiro-Wilk usando a função shapiro.test().

shapiro.test(ToothGrowth$len)

    Shapiro-Wilk normality test

data:  ToothGrowth$len
W = 0.96743, p-value = 0.1091

O \(p\)-valor do teste é 0.1091005 e com isso falhamos em rejeitar a hipótese nula de que len é distribuída conforma uma distribuição Normal. Ou seja, pressuposto de normalidade não violado.

Avançando para o pressuposto de homogeneidade de variâncias, também já coberto na tutorial de \(p\)-valores, pode ser testado com o teste de Levene usando a função leveneTest() da biblioteca {car}.

library(car)
leveneTest(len ~ supp, data = ToothGrowth)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1  1.2136 0.2752
      58               

leveneTest(len ~ dose, data = ToothGrowth)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2  0.6457 0.5281
      57               

O \(p\)-valor de ambos testes para a homogeneidade de variâncias de len nos grupos de supp e dose são respectivamente 0.28 e 0.53. Com isso falhamos em rejeitar a hipótese nula de que len possui variâncias homogêneas nos grupos tanto de supp quanto de dose. Ou seja, pressuposto de homogeneidade de variâncias não violado.

ANOVA Unidirecional⁴

A ANOVA mais simples é chamada de ANOVA Unidirecional que examina a influência de uma variável independente categórica em uma variável contínua dependente.

O R possui uma função padrão para calcular ANOVAs aov() e sua funcionalidade é muito similar à outras funções que já vimos de teste de hipótese, sendo que é necessário fornecer dois argumentos:

1. Fórmula designando a variável cuja média deve ser analisada e os grupos em relação aos quais as médias serão analisadas. A fórmula é designada pela seguinte síntaxe: variavel ~ grupo.
2. O dataset no qual deverá ser encontrados tanto a varíavel quanto os grupos.

aov() quer dizer Analysis of Variance.

A saída da função aov() é um objeto aov que pode ser passado para uma função summary() eu nos trás os resultados da ANOVA.

fit1 <- aov(len ~ supp, data = ToothGrowth)
summary(fit1)

            Df Sum Sq Mean Sq F value Pr(>F)  
supp         1    205  205.35   3.668 0.0604 .
Residuals   58   3247   55.98                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Podemos ver que a diferença do comprimento dos dentes len conforme o método de dosagem supp (suco de laranja vs ácido ascórbico) não é estatisticamente significante (\(p>0.06\)). Ao comparar o nível de significância do teste (\(p=0.06\)) com o limiar estabelecido (\(p<0.05\)) não conseguimos rejeitar a hipótese nula de que não há diferença no comprimento dos dentes.

fit2 <- aov(len ~ dose, data = ToothGrowth)
summary(fit2)

            Df Sum Sq Mean Sq F value   Pr(>F)    
dose         2   2426    1213   67.42 9.53e-16 ***
Residuals   57   1026      18                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Porém, o comprimento dos dentes len muda conforme o tamanho da dose dose (0.5, 1.0 ou 2.0 mg) (\(p<0.05\)). Ao comparar o nível de significância do teste (\(p=0.00000000000000095\)) com o limiar estabelecido (\(p<0.05\)) conseguimos rejeitar a hipótese nula de que não há diferença no comprimento dos dentes.

ANOVA Bidirecional⁵

A ANOVA Bidirecional é uma extensão da ANOVA Unidirecional que examina a influência de duas variáveis independentes categóricas em uma variável contínua dependente. Há duas maneiras de analisarmos essa influência:

• Efeitos principais: efeito de uma (ou mais) variável(is) independente(s) em uma variável dependente. Chamamos esses efeitos de aditivos pois podem ser quebrados em dois efeitos distintos e únicos que estão influenciando a variável dependente.
• Efeitos de interações: quando o efeito de uma (ou mais) variável(is) independente(s) em uma variável dependente é afetado pelo nível de outras variável(is) independente(s). Efeitos de interação não são aditivos pois podem ser quebrados em dois efeitos distintos e únicos que estão influenciando a variável dependente. Há uma interação entre as variáveis independentes.

ANOVA Bidirecional com efeitos principais⁶

Primeiro vamos executar uma ANOVA bidirecional com apenas efeitos principais. Usamos a mesma função aov() do R que gerará o mesmo objeto aov, porém agora precisamos incluir uma segunda variável independente. Fazemos isso incluindo na fórmula a segunda variável junto com a primeira e um sinal positivo de adição + indicando que as duas variáveis devem ser usadas como efeitos principais na análise:

fit3 <- aov(len ~ supp + dose, data = ToothGrowth)
summary(fit3)

            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4   14.02 0.000429 ***
dose         2 2426.4  1213.2   82.81  < 2e-16 ***
Residuals   56  820.4    14.7                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pelos resultados, podemos ver que tanto supp e dose são estatisticamente significantes. Sendo que dose possui o maior tamanho de efeito (F value) 124.0 contra 11.4 de supp.

ANOVA Bidirecional com efeitos de interação⁷

Para executarmos uma ANOVA bidirecional com efeitos de interações. Usamos novamente função aov() do R que gerará o mesmo objeto aov, porém agora precisamos incluir uma segunda variável independente e especificar a interação. Fazemos isso incluindo na fórmula a segunda variável junto com a primeira e um sinal de multiplicação⁸ * indicando que as duas variáveis devem ser usadas como efeitos principais e também de interação na análise:

fit4 <- aov(len ~ supp * dose, data = ToothGrowth)
summary(fit4)

            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4  15.572 0.000231 ***
dose         2 2426.4  1213.2  92.000  < 2e-16 ***
supp:dose    2  108.3    54.2   4.107 0.021860 *  
Residuals   54  712.1    13.2                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Como resultado vemos que os efeitos principais tanto de supp e dose se mantiveram com \(p\)-valores e tamanho de efeitos similares. Mas a grande novidade agora é que a interação supp:dose também é estatisticamente significante. Nesse caso devemos usar a ANOVA com efeito de interação e não a ANOVA com efeitos principais. Caso a interação supp:dose não fosse estatisticamente significante deveríamos usar a ANOVA com efeitos principais e não a ANOVA com efeito de interação.

ANOVA Não-Paramétrica – Teste Kruskal-Wallis⁹

O que fazer se minha variável dependente viola os pressupostos de normalidade ou de homogeneidade de variâncias? Nesse caso devemos usar uma abordagem não-paramétrica. A ANOVA clássica é uma abordagem paramétrica: depende fortemente da suposição que os dados estejam distribuídos de acordo com uma distribuição específica e que as variâncias entre os grupos é igual. Testes não-paramétricos não fazem suposições sobre a distribuição dos dados e portanto podem ser usados quando os pressupostos dos testes paramétricos são violados.

Atenção: testes não-paramétricos são menos sensíveis em rejeitar a hipótese nula quando ela é verdadeira (erro tipo I) do que testes paramétricos quando o pressuposto de normalidade não é violado (Zimmerman, 1998). Então não pense que deve sempre aplicar um teste não-paramétrico em todas as ocasiões.

A versão não-paramétrica da ANOVA é o teste de Kruskal-Wallis (também chamado de teste de Kruskal-Wallis por postos ou teste H de Kruskal-Wallis) foi desenvolvido em 1952 por William Kruskal e W. Allen Wallis (Kruskal & Wallis, 1952). O teste pode ser encontrada na função padrão que vem com o R kruskal.test() e funciona identicamente a aov(), com a exceção de que aceita somente uma variável independente. kruskal.test() aceita dois argumentos:

Não é recomendado empregar ANOVAS bidirecionais não-paramétricas. Caso o leitor precise usar uma técnica não-paramétrica para mais de duas variáveis independentes, recomendamos um abordagem que empregue algum modelo linear (tutorial 6) ou modelo linear generalizado (tutorial 7).

1. Fórmula designando a variável cuja média deve ser analisada e os grupos em relação aos quais as médias serão analisadas. A fórmula é designada pela seguinte síntaxe: variavel ~ grupo.
2. O dataset no qual deverá ser encontrados tanto a varíavel quanto os grupos.

Aqui vamos fazer apenas o exemplo com supp usando o dataset ToothGrowth:

kruskal.test(len ~ supp, data = ToothGrowth)

    Kruskal-Wallis rank sum test

data:  len by supp
Kruskal-Wallis chi-squared = 3.4454, df = 1, p-value = 0.06343

Como podem ver, o resultado é o mesmo que o da ANOVA paramétrica aov().

ANOVA de Medidas Repetidas¹⁰

Caso você esteja procurando por uma extensão natural ao teste \(t\) para duas amostras pareadas na ANOVA. Sim, ela existe e se chama ANOVA de Medidas Repetidas, mas nós recomendamos fortemente que você não use ANOVA de Medidas Repetidas.

Há bastante evidências que demonstram a inadequação de ANOVAs de medidas repetidas (Camilli & Shepard, 1987; Chang, Pal, Lim, & Lin, 2010; Levy, 1978; Vasey & Thayer, 1987). Diversas referências sugerem trocar a ANOVA de medidas repetidas por um modelo logístico misto (Jaeger, 2008; Kristensen & Hansen, 2004), que se demonstrou mais flexível, acurado e sensível.

Não vamos abordar modelos mistos nos tutoriais. Caso esteja interessado veja a função lme() da biblioteca {nlme}.

Comparações Múltiplas entre Grupos

Embora ANOVA seja uma abordagem paramétrica poderosa e útil para analisar dados aproximadamente normalmente distribuídos com mais de dois grupos, ela não fornece nenhuma visão mais profunda dos padrões ou comparações entre grupos específicos.

Após analisar os resultados de uma ANOVA, é muito comum realizar uma comparação post-hoc usando um conjunto de técnicas comparativas de média entre grupos que controlam a taxa de erro familiar. A principal técnica paramétrica é o teste de Tukey e a principal técnica não-paramétrica é o teste de Dunn.

Teste de Tukey¹¹

Um método comum e popular de análise post-hoc é o Teste de Tukey. O teste é conhecido por vários nomes diferentes: teste de Tukey da diferença honestamente significativa, teste de Tukey da diferença totalmente significativa, entre outros… O teste de Tukey compara as médias de todos os grupos entre si e é considerado o melhor método disponível nos casos em que os intervalos de confiança são desejados ou se os tamanhos das amostras são desiguais.

A estatística de teste usada no teste de Tukey é denotada \(q\) e é essencialmente uma estatística \(t\) modificada que corrige múltiplas comparações.

O teste de Tukey pode ser encontrado na função padrão que vem com o R tukeyHSD() e aceita como argumento um objeto aov resultante de uma ANOVA:

TukeyHSD(fit3)

Como resultado temos uma tabela com todos os grupos das variáveis independentes da ANOVA testados entre si:

• diff – diferença entre os grupos.
• lwr – intervalo de confiança 95% inferior da diferença.
• upr – intervalo de confiança 95% superior da diferença.
• p adj – estatística \(q\) do Teste de Tukey, aqui referida como um \(p\)-valor ajustado.

Teste de Dunn¹²

O teste de Tukey assume que a variável dependente é normalmente distribuída e, portanto, não é apropriado como um teste post-hoc após um teste não-paramétrico como Kruskal-Wallis. O único teste post-hoc não paramétrico para esse contexto é o teste de Dunn(Dunn, 1964).

Para executar o teste de Dunn é necessário usar a função DunnTest() da biblioteca {DescTools} (Andri et mult. al., 2020). Ela aceita argumentos similares à função kruskal.test():

1. Fórmula designando a variável cuja média deve ser analisada e os grupos em relação aos quais as médias serão analisadas. A fórmula é designada pela seguinte síntaxe: variavel ~ grupo.
2. O dataset no qual deverá ser encontrados tanto a varíavel quanto os grupos.

library(DescTools)
DunnTest(len ~ dose, data = ToothGrowth)

 Dunn's test of multiple comparisons using rank sums : holm  

      mean.rank.diff    pval    
1-0.5         19.625 0.00076 ***
2-0.5         35.125   6e-10 ***
2-1           15.500 0.00499 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Uma coisa importante de se notar é que não é possível obter um intervalo de confiança de um teste de Dunn.

Como visualizar ANOVAs com R

Mais uma vez vamos recorrer a biblioteca {ggpubr} (Kassambara, 2020) para visualização de testes estatísticos. Veja um exemplo abaixo com o dataset ToothGrowth.

Adicionamos a camada das estatísticas de comparação dos grupos com o stat_compare_means() especificando que tipo de método será utilizado na análise:

• "anova" – ANOVA.
• "kruskal.test" – ANOVA não paramétrica.

library(ggpubr)
ggboxplot(ToothGrowth, x = "dose", y = "len",
                color = "supp", palette = "lancet",
                add = "jitter", shape = "dose") +
  stat_compare_means(method = "anova")

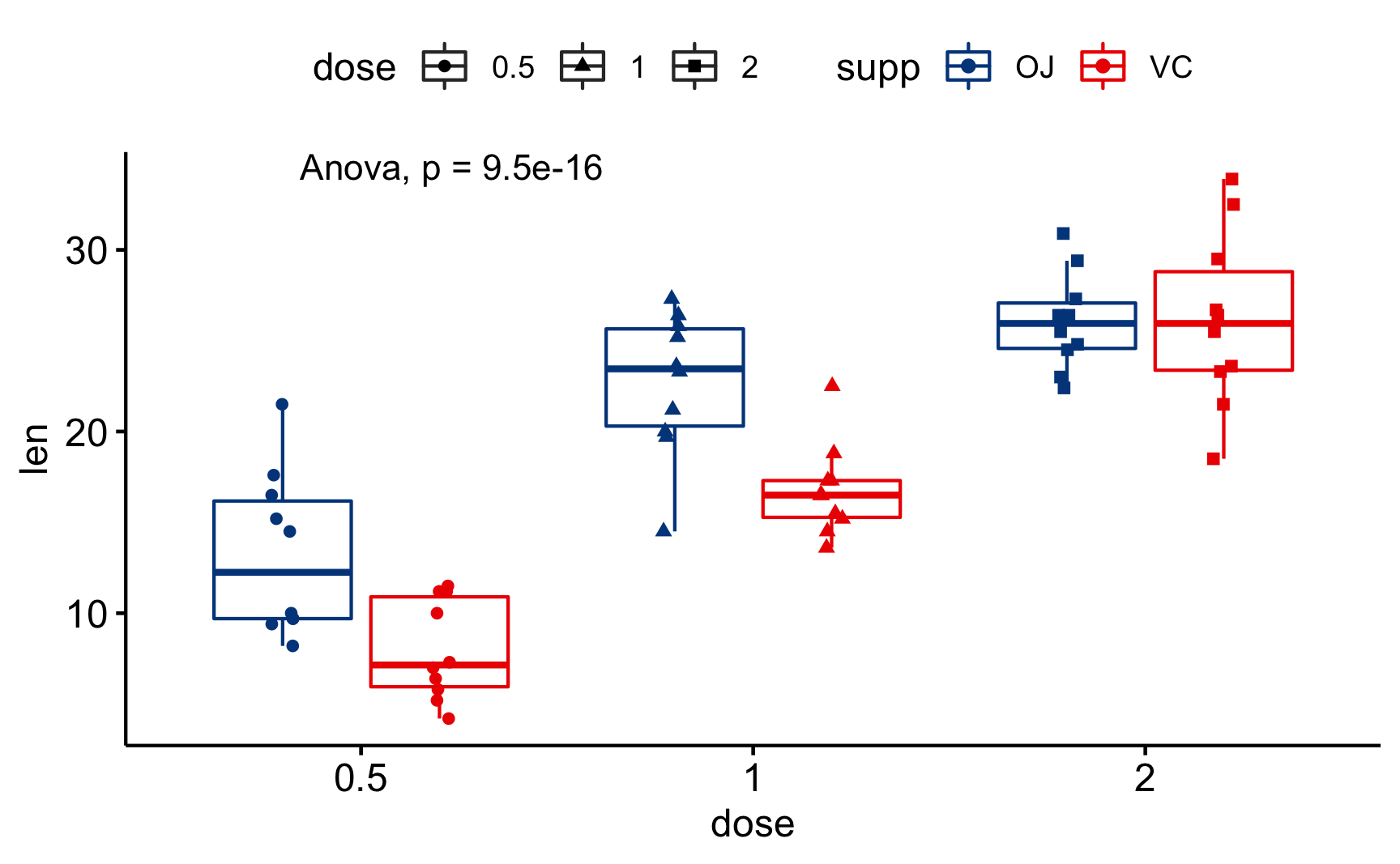
Figure 2: Diagrama de Caixa usando o {ggpubr} – ANOVA

library(ggpubr)
ggboxplot(ToothGrowth, x = "dose", y = "len",
                color = "supp", palette = "lancet",
                add = "jitter", shape = "dose") +
  stat_compare_means(method = "kruskal.test")

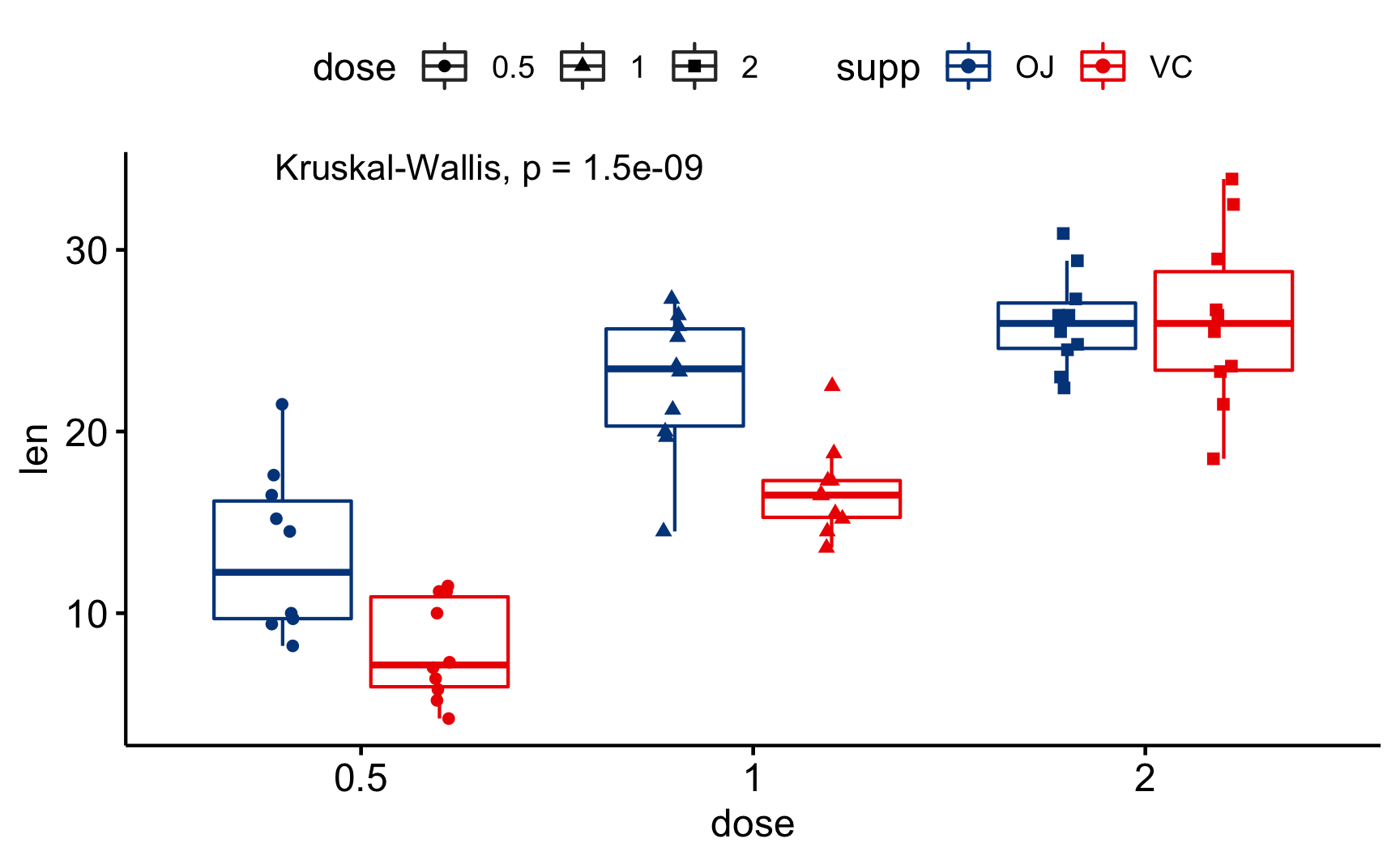
Figure 3: Diagrama de Caixa usando o {ggpubr} – ANOVA Não-Paramétrica

Ambiente

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] DescTools_0.99.40  skimr_2.1.2        ggpubr_0.4.0      
 [4] car_3.0-10         carData_3.0-4      patchwork_1.1.1   
 [7] dplyr_1.0.4        ggplot2_3.3.3      DiagrammeR_1.0.6.1
[10] readxl_1.3.1      

loaded via a namespace (and not attached):
 [1] lubridate_1.7.9.2  RColorBrewer_1.1-2 rprojroot_2.0.2   
 [4] ggsci_2.9          repr_1.1.3         tools_4.0.3       
 [7] backports_1.2.1    utf8_1.1.4         R6_2.5.0          
[10] DBI_1.1.1          colorspace_2.0-0   withr_2.4.1       
[13] tidyselect_1.1.0   Exact_2.1          downlit_0.2.1     
[16] curl_4.3           compiler_4.0.3     cli_2.3.0         
[19] expm_0.999-6       xml2_1.3.2         labeling_0.4.2    
[22] bookdown_0.21      scales_1.1.1       mvtnorm_1.1-1     
[25] stringr_1.4.0      digest_0.6.27      foreign_0.8-80    
[28] rmarkdown_2.6      rio_0.5.16         base64enc_0.1-3   
[31] pkgconfig_2.0.3    htmltools_0.5.1.1  highr_0.8         
[34] htmlwidgets_1.5.3  rlang_0.4.10       rstudioapi_0.13   
[37] visNetwork_2.0.9   farver_2.0.3       generics_0.1.0    
[40] jsonlite_1.7.2     zip_2.1.1          distill_1.2       
[43] magrittr_2.0.1     Matrix_1.2-18      Rcpp_1.0.6        
[46] munsell_0.5.0      fansi_0.4.2        abind_1.4-5       
[49] reticulate_1.18    lifecycle_0.2.0    stringi_1.5.3     
[52] yaml_2.2.1         rootSolve_1.8.2.1  MASS_7.3-53       
[55] grid_4.0.3         forcats_0.5.1      crayon_1.4.1      
[58] lmom_2.8           lattice_0.20-41    haven_2.3.1       
[61] hms_1.0.0          knitr_1.31         pillar_1.4.7      
[64] boot_1.3-25        gld_2.6.2          ggsignif_0.6.0    
[67] glue_1.4.2         evaluate_0.14      data.table_1.13.6 
[70] vctrs_0.3.6        cellranger_1.1.0   gtable_0.3.0      
[73] purrr_0.3.4        tidyr_1.1.2        assertthat_0.2.1  
[76] xfun_0.21          openxlsx_4.2.3     broom_0.7.4       
[79] e1071_1.7-4        rstatix_0.6.0      class_7.3-17      
[82] tibble_3.0.6       ellipsis_0.3.1    

---

1. O número de testes pode ser calculado pela combinação de \(n\) grupos tomados 2 a 2 \({n \choose 2}\), então para 3 grupos temos 3 testes, para 4 grupos 6 testes e assim por diante…↩︎

2. Termo inglês: Family-wise error rate – FWER.↩︎

3. Sim, o mesmo Fisher da tutorial de \(p\)-valores. Mais uma contribuição crucial para a ciência e Estatística. Lembrando que Fisher possuía uma visão muito forte sobre etnia e raça preconizando a superioridade de certas etnias.↩︎

4. Termo inglês: One-Way ANOVA.↩︎

5. Termo inglês: Two-Way ANOVA.↩︎

6. Termo inglês: Main Effects Two-Way ANOVA.↩︎

7. Termo inglês: Interaction Effects Two-Way ANOVA.↩︎

8. matematicamente falando interação é uma multiplicação entre as duas variáveis independentes↩︎

9. Termos inglês: Kruskal–Wallis test by ranks ou Kruskal–Wallis H test.↩︎

10. Termo inglês: Repeated Measures ANOVA↩︎

11. Termo inglês: Tukey’s HSD (honestly significant difference) test.↩︎

12. Termo inglês: Dunn’s Test.↩︎