Likert e Escalas Ordinais

Como trabalhar com escalas Likert e dados ordinais.

Jose Storopoli https://scholar.google.com/citations?user=xGU7H1QAAAAJ&hl=en (UNINOVE)https://www.uninove.br , Leonardo Vils https://scholar.google.com/citations?user=VO07L9EAAAAJ&hl=en (UNINOVE)https://www.uninove.br
January 11, 2021

Os dados ordinais são frequentemente analisados como se fossem métricos. Porém, a análise de dados ordinais como se fossem métricos pode sistematicamente levar a erros como falsos positivos (ou seja, detectando um efeito onde não existe nenhum, erros Tipo I), falsos negativos (ou seja, perda de poder estatístico, erros Tipo II); e até mesmo uma inversão de efeitos (efeitos positivos podem virar efeitos negativos) (Bürkner & Vuorre, 2019; Liddell & Kruschke, 2018).

Primeiramente apresentaremos o que são dados ordinais e como eles diferem de dados métricos. Na sequência abordaremos a principal origem de dados ordinais em pesquisas (escala Likert). E por fim, mostraremos uma alternativa à regressão linear que é mais indicada para dados ordinais: regressão ordinal.

Dados Ordinais

Dados ordinais são um tipo de dados categóricos e estatísticos em que as variáveis têm categorias naturais ordenadas e as distâncias entre as categorias não são conhecidas. A principal diferença entre os dados métricos e categóricos é justamente a questão da distância. Em dados métricos a distância entre 1 e 2 é a mesma entre 2 e 3. Porém, em dados categóricos tal distância não é assumida como igual ou conhecida. Portanto a distância entre uma categoria \(X_1\) e uma categoria \(X_2\) não é a mesma da distância entre a categoria \(X_2\) e uma categoria \(X_3\).

Para exemplificar a diferença entre dados métricos e ordinais, veja a figura 1 que mostra dados ordinais em uma representação métrica de uma distribuição normal. É possível ver que cada valor de 1 a 5 (items de uma escala Likert, por exemplo) é mapeado para um ponto específico da distribuição normal. Além disso, a distância entre tais mapeamentos é a mesma, ou seja, as mensurações são equidistantes.

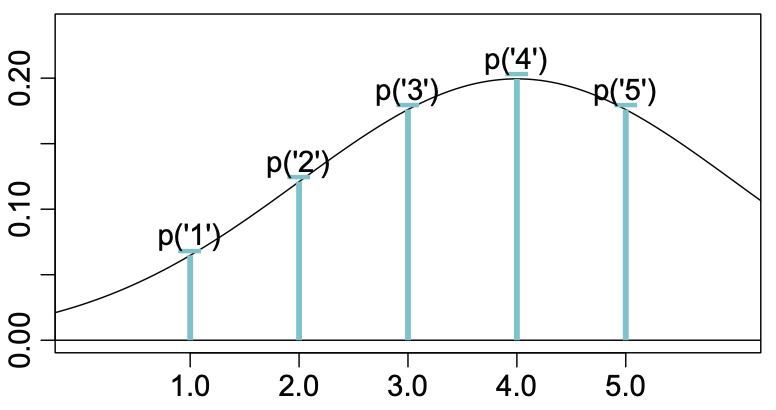
Modelo Métrico. Figura adaptada de @liddellAnalyzingOrdinalData2018

Figure 1: Modelo Métrico. Figura adaptada de Liddell & Kruschke (2018)

Já na figura 2 mostramos o modelo latente ordinal. Neste modelo os dados ordinais são representados de maneira discreta (gráfico de barras na parte superior) e não de maneira contínua como o modelo métrico. Além disso, os valores são mapeados para uma variável latente (não-observada) de uma distribuição normal que é contínua (histograma na parte inferior). Vejam que a direção da seta indica a causalidade dos dados. As opções discretas 1, 2, 3, 4 e 5 são originárias em uma variável latente contínua e se manifestam como opções discretas do respondente. Notem que no modelo latente ordinal as distâncias entre os mapeamentos na variável latente não são equidistantes.

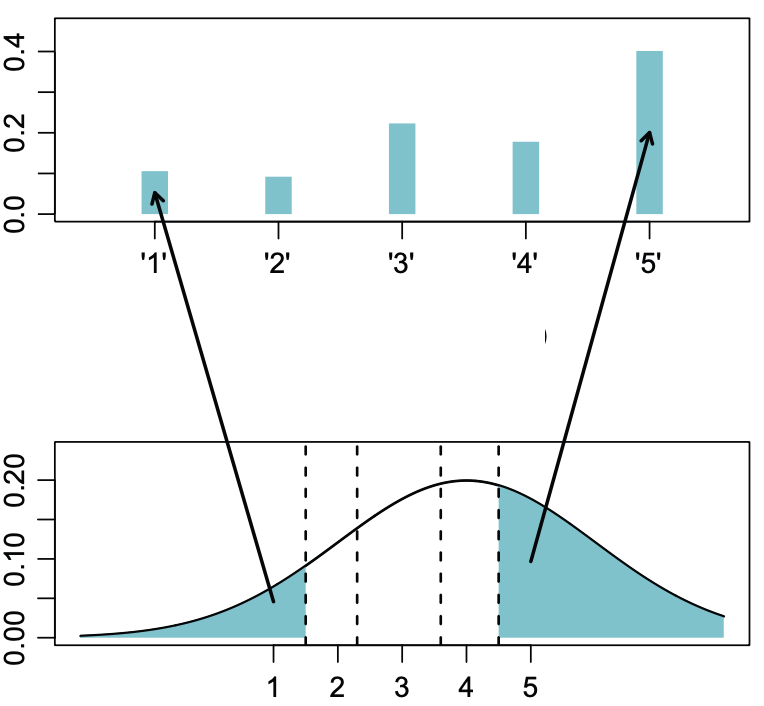
Modelo Latente Ordenado. Figura adaptada de @liddellAnalyzingOrdinalData2018

Figure 2: Modelo Latente Ordenado. Figura adaptada de Liddell & Kruschke (2018)

Escala Likert

Nas ciências sociais temos um predomínio de escalas ordinais como maneiras de mensuração de opinião. Dentre as diversas maneiras de mensurar opiniões, a escala Likert é a escala mais utilizada por pesquisadores e cientistas. A escala Likert foi criada em 1932 por Rensis Likert (figura 3) na sua tese de doutorado como uma forma de identificar a extensão das atitudes e sentimentos de uma pessoa em relação à assuntos internacionais. Após isso, a escala Likert se tornou o principal instrumento quando usamos perguntas para a qual a resposta é indicada em uma escala ordenada discreta que varia de um ponto final qualitativo a outro ponto final qualitativo (por exemplo, discordo totalmente para concordar totalmente).

Rensis Likert. Figura de https://www.wikipedia.org

Figure 3: Rensis Likert. Figura de https://www.wikipedia.org

As escalas Likert normalmente têm de 4 a 7 opções de resposta discretas. Um ponto importante é que escalas Likert ímpares permitem com que o respondente escolha uma opção neutra, em outras palavras, o respondente pode escolher ficar “em cima do muro.” Abaixo um exemplo de uma escala Likert ímpar, de “Discordo Fortemente” até “Concordo Fortemente.” Vejam que há a opção neutra (0) “Não Discordo nem Concordo.”

Discordo Fortemente Discordo Não Discordo nem Concordo Concordo Concordo Fortemente
-2 -1 0 1 2

Já escalas Likert pares não permitem com que respondente escolha uma opção neutra. Elas forçam o respondente a escolher uma polaridade positiva ou negativa. Abaixo um exemplo de uma escala Likert par, de “Discordo Fortemente” até “Concordo Fortemente.” Vejam que há a opção neutra (0) como na escala ímpar.

Discordo Fortemente Discordo Concordo Concordo Fortemente
-2 -1 1 2

Como aplicar uma Regressão Ordinal no R

Para demonstrar dados ordinais, usaremos a biblioteca {likert} (Bryer & Speerschneider, 2016) que possui o dataset pisaitems que contém resultados do Programme of International Student Assessment (PISA) de 2009 para a América do Norte (Estados Unidos, Canadá e México). Vamos apenas utilizar as 11 questões do grupo de perguntas 24 sobre atitudes de alunos:

  1. ST24Q01 I read only if I have to. – Eu leio apenas se for necessário.
  2. ST24Q02 Reading is one of my favorite hobbies. – Ler é um dos meus passatempos favoritos.
  3. ST24Q03 I like talking about books with other people. – Gosto de conversar sobre livros com outras pessoas.
  4. ST24Q04 I find it hard to finish books. – Acho difícil terminar livros.
  5. ST24Q05 I feel happy if I receive a book as a present. – Fico feliz se recebo um livro de presente.
  6. ST24Q06 For me, reading is a waste of time. – Para mim, ler é perda de tempo.
  7. ST24Q07 I enjoy going to a bookstore or a library. – Gosto de ir a uma livraria ou biblioteca.
  8. ST24Q08 I read only to get information that I need. – Eu leio apenas para obter as informações de que preciso.
  9. ST24Q09 I cannot sit still and read for more than a few minutes. – Não consigo ficar parado e ler por mais de alguns minutos.
  10. ST24Q10 I like to express my opinions about books I have read. – Gosto de expressar minhas opiniões sobre os livros que li.
  11. ST24Q11 I like to exchange books with my friends. – Gosto de trocar livros com meus amigos.

Nós, sempre que carregamos um dataset no R, temos o costume de usar a biblioteca {skimr} (Waring et al., 2020) para produzir um sumário dos dados. Como vocês podem ver a escala usada para as perguntas 24 é uma Likert de 4 items: Strongly disagree, Disagree, Agree, Strongly agree.

library(likert)
library(dplyr)
library(skimr)
data(pisaitems)
pisa <- pisaitems %>%
  dplyr::select(starts_with("ST24"))
skim(pisa)
Table 1: Data summary
Name pisa
Number of rows 66690
Number of columns 11
_______________________
Column type frequency:
factor 11
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
ST24Q01 1199 0.98 FALSE 4 Dis: 23515, Agr: 20000, Str: 14947, Str: 7029
ST24Q02 1134 0.98 FALSE 4 Dis: 23811, Agr: 20935, Str: 13323, Str: 7487
ST24Q03 1276 0.98 FALSE 4 Agr: 23525, Dis: 22072, Str: 13900, Str: 5917
ST24Q04 1210 0.98 FALSE 4 Dis: 26449, Agr: 17358, Str: 16343, Str: 5330
ST24Q05 1214 0.98 FALSE 4 Agr: 26304, Dis: 18106, Str: 12625, Str: 8441
ST24Q06 1300 0.98 FALSE 4 Str: 27621, Dis: 26579, Agr: 7177, Str: 4013
ST24Q07 1319 0.98 FALSE 4 Agr: 24111, Dis: 21815, Str: 11663, Str: 7782
ST24Q08 1234 0.98 FALSE 4 Agr: 23407, Dis: 23183, Str: 9806, Str: 9060
ST24Q09 1301 0.98 FALSE 4 Dis: 28201, Str: 21655, Agr: 11063, Str: 4470
ST24Q10 1193 0.98 FALSE 4 Agr: 28702, Dis: 18037, Str: 9892, Str: 8866
ST24Q11 1135 0.98 FALSE 4 Dis: 21648, Agr: 21030, Str: 14762, Str: 8115

A biblioteca {likert} ainda tem uma função bem conveniente para plotar gráficos de dados ordinais que usam escala Likert, veja um exemplo na figura 4.

plot(likert(pisa))
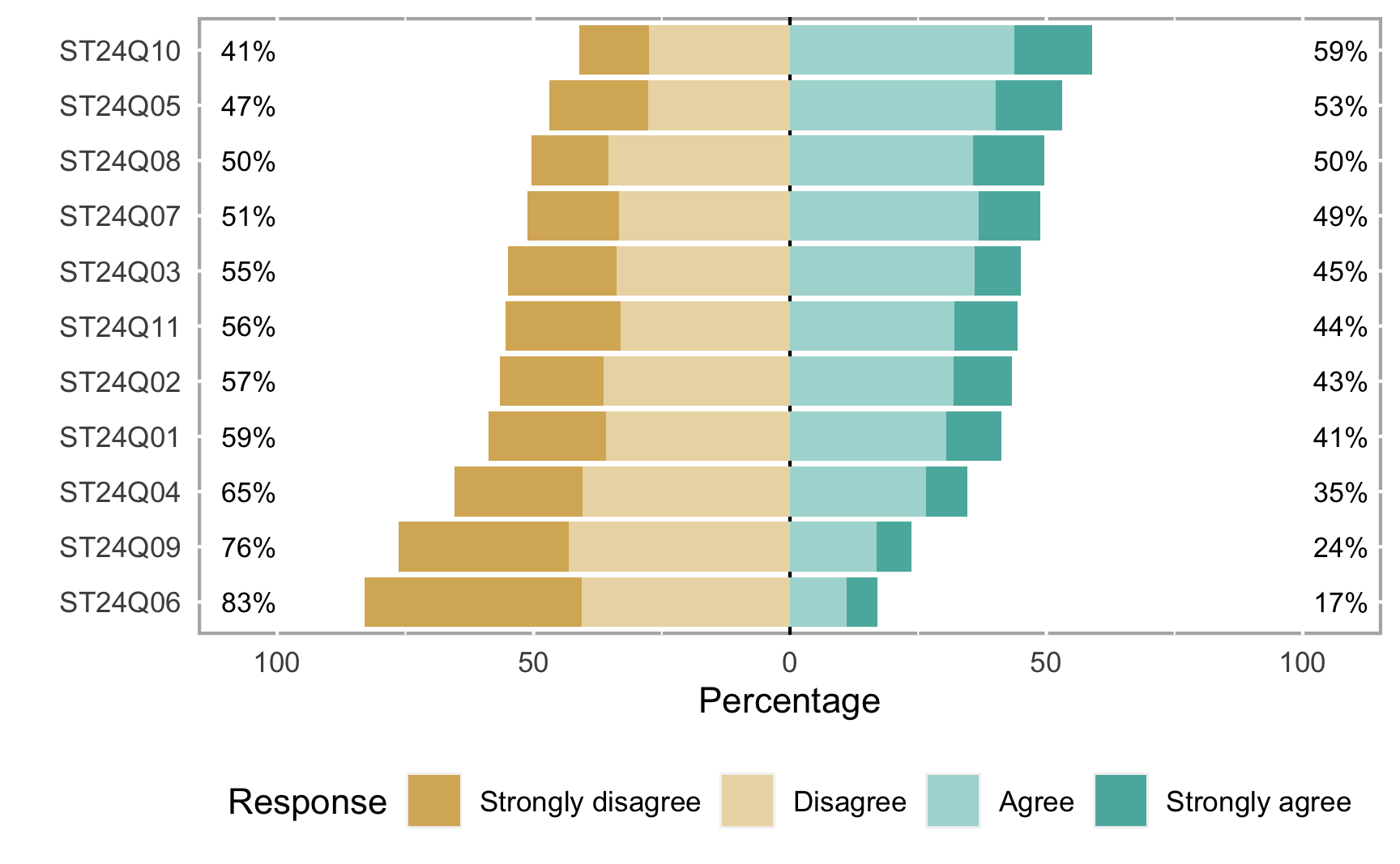
Dados das 11 questões do PISA do grupo de perguntas 24 sobre atitudes de alunos

Figure 4: Dados das 11 questões do PISA do grupo de perguntas 24 sobre atitudes de alunos

Primeiro Cenário – Regressão Linear

Aqui vamos aplicar uma regressão linear para a variável ST24Q02 que é a pergunta Reading is one of my favorite hobbies. (Ler é um dos meus passatempos favoritos). Como variável independente vamos usar o país do aluno CNT (Mexico, EUA ou Canadá). Aqui estamos convertendo a variável ordinal ST24Q02 como numérica (contínua).

linear_reg <- pisaitems %>%
  dplyr::select(CNT, ST24Q02) %>%
  mutate(ST24Q02 = as.numeric(ST24Q02)) %>%
  lm(ST24Q02 ~ CNT, data = .)

summary(linear_reg)


Call:
lm(formula = ST24Q02 ~ CNT, data = .)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.4357 -0.4356 -0.2465  0.5644  1.8932 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       2.246538   0.006126  366.72   <2e-16 ***
CNTMexico         0.189115   0.007744   24.42   <2e-16 ***
CNTUnited States -0.139727   0.014200   -9.84   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.921 on 65553 degrees of freedom
  (1134 observations deleted due to missingness)
Multiple R-squared:  0.01458,   Adjusted R-squared:  0.01455 
F-statistic:   485 on 2 and 65553 DF,  p-value: < 2.2e-16

Como ilustrado no tutorial sobre regressão linear, o resultado pode ser interpretado pela coluna do \(p\)-valor (Pr(>|t|)) e pela coluna do coeficiente estimado (Estimate). Vemos que, na amostra de 2009, alunos do México concordam muito mais com a frase que “Ler é um dos meus passatempos favoritos” do que alunos do Canadá (categoria basal de comparação). E alunos dos Estados Unidos discordam muito mais que alunos do Canadá.

Segundo Cenário – Regressão Ordinal

Para o segundo cenário vamos usar os mesmos dados do primeiro só que agora estamos usando a função polr() da biblioteca {MASS} (Venables & Ripley, 2002) que aplica uma regressão ordinal. Vejam que aqui não precisamos converter a variável ST24Q02 como numérica, pois polr() aceita (e prefere) uma variável ordinal como variável dependente. Além disso precisamos especificar a função de ligação que irá fazer a inferência da regressão com o argumento method. O padrão é a função logit ("logistic") que é o inverso da função logística, mas no nosso caso especificamos a função de ligação probit ("probit") que é o inverso da função de distribuição normal acumulada padrão, pois acreditamos que a variável latente por trás da ST24Q02 segue uma distribuição normal. Uma última observação: o argumento Hess é necessário ser TRUE caso queira extrair um sumário da regressão com summary().

library(MASS)
ordinal_reg <- pisaitems %>%
  dplyr::select(CNT, ST24Q02) %>%
  polr(ST24Q02 ~ CNT, data = ., Hess = TRUE, method = "probit")
summary(ordinal_reg)

Call:
polr(formula = ST24Q02 ~ CNT, data = ., Hess = TRUE, method = "probit")

Coefficients:
                   Value Std. Error t value
CNTMexico         0.2184    0.00902  24.218
CNTUnited States -0.1620    0.01662  -9.743

Intercepts:
                           Value    Std. Error t value 
Strongly disagree|Disagree  -0.7247   0.0079   -91.5349
Disagree|Agree               0.2855   0.0077    37.0243
Agree|Strongly agree         1.3262   0.0088   151.3259

Residual Deviance: 170017.64 
AIC: 170027.64 
(1134 observations deleted due to missingness)

Como vocês podem ver o resultado da regressão ordinal é diferente. A regressão ordinal possui (no nosso caso) três constantes (intercepts) mapeando aonde na variável latente o limiar de cada valor ordinal foi mapeado. Além disso, o valor do coeficiente para México e Estados Unidos são maiores em termos absolutos, demonstrando uma melhor sensibilidade (poder estatístico) da regressão ordinal do que a regressão linear em dados ordinais.

Cenários mais Complexos

Caso o leitor queira experimentar com modelos de regressão ordinais mais complexos sugerimos a biblioteca {ordinal} (Christensen, 2019) que permite modelos ordinais complexos frequentistas e a biblioteca {brms} (Bürkner, 2018) que permite modelos ordinais complexos Bayesianos. Ambas bibliotecas possuem diversas funções de ligação e também é possível especificar modelos multiníveis (também chamados de modelos hierárquicos, modelos mistos, modelos de dois estágios etc.)

Comentários Finais

Dados ordinais, especialmente mensurados por escala Likert, aparecem com muita frequência em pesquisas. Tratar dados ordinais como se fossem métricos (contínuos) não é apropriado e portanto regressão linear não é a técnica correta quando a variável dependente é ordinal. Para isso recomendamos a regressão ordinal.

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] MASS_7.3-53          likert_1.3.5         xtable_1.8-4        
 [4] naniar_0.6.0.9000    purrr_0.3.4          gtsummary_1.3.6     
 [7] gt_0.2.2             lm.beta_1.5-1        lmtest_0.9-38       
[10] zoo_1.8-8            ggfortify_0.4.11     sjPlot_2.8.7        
[13] broom_0.7.4          palmerpenguins_0.1.0 magrittr_2.0.1      
[16] mnormt_2.0.2         cowplot_1.1.1        tidyr_1.1.2         
[19] DescTools_0.99.40    skimr_2.1.2          ggpubr_0.4.0        
[22] car_3.0-10           carData_3.0-4        patchwork_1.1.1     
[25] dplyr_1.0.4          ggplot2_3.3.3        DiagrammeR_1.0.6.1  
[28] readxl_1.3.1        

loaded via a namespace (and not attached):
  [1] backports_1.2.1     plyr_1.8.6          repr_1.1.3         
  [4] splines_4.0.3       usethis_2.0.1       digest_0.6.27      
  [7] htmltools_0.5.1.1   magick_2.6.0        fansi_0.4.2        
 [10] checkmate_2.0.0     openxlsx_4.2.3      modelr_0.1.8       
 [13] colorspace_2.0-0    haven_2.3.1         xfun_0.21          
 [16] crayon_1.4.1        jsonlite_1.7.2      Exact_2.1          
 [19] lme4_1.1-26         survival_3.2-7      glue_1.4.2         
 [22] gtable_0.3.0        emmeans_1.5.4       sjstats_0.18.1     
 [25] sjmisc_2.8.6        abind_1.4-5         scales_1.1.1       
 [28] mvtnorm_1.1-1       DBI_1.1.1           rstatix_0.6.0      
 [31] ggeffects_1.0.1     Rcpp_1.0.6          performance_0.7.0  
 [34] tmvnsim_1.0-2       reticulate_1.18     foreign_0.8-80     
 [37] htmlwidgets_1.5.3   RColorBrewer_1.1-2  ellipsis_0.3.1     
 [40] pkgconfig_2.0.3     farver_2.0.3        sass_0.3.1         
 [43] utf8_1.1.4          reshape2_1.4.4      tidyselect_1.1.0   
 [46] labeling_0.4.2      rlang_0.4.10        effectsize_0.4.3   
 [49] munsell_0.5.0       cellranger_1.1.0    tools_4.0.3        
 [52] visNetwork_2.0.9    cli_2.3.0           generics_0.1.0     
 [55] sjlabelled_1.1.7    evaluate_0.14       stringr_1.4.0      
 [58] yaml_2.2.1          fs_1.5.0            knitr_1.31         
 [61] zip_2.1.1           visdat_0.5.3        rootSolve_1.8.2.1  
 [64] nlme_3.1-149        xml2_1.3.2          compiler_4.0.3     
 [67] rstudioapi_0.13     curl_4.3            e1071_1.7-4        
 [70] ggsignif_0.6.0      tibble_3.0.6        statmod_1.4.35     
 [73] broom.helpers_1.1.0 stringi_1.5.3       highr_0.8          
 [76] parameters_0.11.0   forcats_0.5.1       lattice_0.20-41    
 [79] Matrix_1.2-18       psych_2.0.12        commonmark_1.7     
 [82] nloptr_1.2.2.2      ggsci_2.9           vctrs_0.3.6        
 [85] norm_1.0-9.5        pillar_1.4.7        lifecycle_0.2.0    
 [88] estimability_1.3    data.table_1.13.6   insight_0.12.0     
 [91] lmom_2.8            R6_2.5.0            bookdown_0.21      
 [94] gridExtra_2.3       rio_0.5.16          gld_2.6.2          
 [97] distill_1.2         boot_1.3-25         assertthat_0.2.1   
[100] rprojroot_2.0.2     withr_2.4.1         parallel_4.0.3     
[103] mgcv_1.8-33         bayestestR_0.8.2    expm_0.999-6       
[106] hms_1.0.0           grid_4.0.3          class_7.3-17       
[109] minqa_1.2.4         rmarkdown_2.6       downlit_0.2.1      
[112] lubridate_1.7.9.2   base64enc_0.1-3
Bryer, J., & Speerschneider, K. (2016). Likert: Analysis and visualization likert items. Retrieved from https://CRAN.R-project.org/package=likert
Bürkner, P.-C. (2018). Advanced Bayesian multilevel modeling with the R package brms. The R Journal, 10(1), 395–411. https://doi.org/10.32614/RJ-2018-017
Bürkner, P.-C., & Vuorre, M. (2019). Ordinal Regression Models in Psychology: A Tutorial. Advances in Methods and Practices in Psychological Science, 2(1), 77–101. https://doi.org/10.1177/2515245918823199
Christensen, R. H. B. (2019). Ordinal—regression models for ordinal data.
Liddell, T. M., & Kruschke, J. K. (2018). Analyzing ordinal data with metric models: What could possibly go wrong? Journal of Experimental Social Psychology, 79, 328–348. https://doi.org/10.1016/j.jesp.2018.08.009
Venables, W. N., & Ripley, B. D. (2002). Modern applied statistics with s (Fourth). Retrieved from http://www.stats.ox.ac.uk/pub/MASS4/
Waring, E., Quinn, M., McNamara, A., Arino de la Rubia, E., Zhu, H., & Ellis, S. (2020). Skimr: Compact and flexible summaries of data. Retrieved from https://CRAN.R-project.org/package=skimr

References

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY-SA 4.0. Source code is available at https://github.com/storopoli/Estatistica, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Storopoli & Vils (2021, Jan. 11). Estatística com R: Likert e Escalas Ordinais. Retrieved from https://storopoli.github.io/Estatistica/aux-Likert.html

BibTeX citation

@misc{storopoli2021likertR,
  author = {Storopoli, Jose and Vils, Leonardo},
  title = {Estatística com R: Likert e Escalas Ordinais},
  url = {https://storopoli.github.io/Estatistica/aux-Likert.html},
  year = {2021}
}

© Copyright 2021 Jose Storopoli & Leonardo Vils.

Content licensed under the CC BY-SA 4.0.