Relação entre Variáveis – Correlações

Como que descrevemos a força de associação entre duas variáveis.

Correlações nos indicam a magnitude de associação que duas variáveis possuem. É uma métrica simétrica, isto quer dizer que a correlação entre \(X\) e \(Y\), \(\text{corr}(X,Y)\), é a mesma que a correlação entre \(Y\) e \(X\), \(\text{corr}(Y,X)\). Além disso é uma métrica padronizada entre -1 e +1:

• -1: correlação negativa perfeita.
• +1: correlação positiva perfeita.

Correlações e Desvio Padrão

Desvio padrão é uma métrica descritiva de uma variável que indica a magnitude de variação (dispersão de uma centralidade) que uma variável possui. Veja o exemplo da figura 1, na qual temos três distribuições Normais com a mesma média 0, porém com desvio padrões diferentes. Quanto maior o desvio padrão, maior será a variação de uma variável.

library(ggplot2)
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
  mapply(function(mean, sd, col) {
    stat_function(fun = dnorm,
                  args = list(mean = mean,
                              sd = sd),
                  aes(col = col), size = 3)
  },
  mean = rep(0, 3),
  sd = c(1, .5, 2),
  col = c("1", "0.5", "2")) +
  scale_colour_brewer("Desvio\nPadrão", palette = "Set1",
                      guide = guide_legend(ncol = 1,
                                           nrow = 3,
                                           byrow = TRUE))

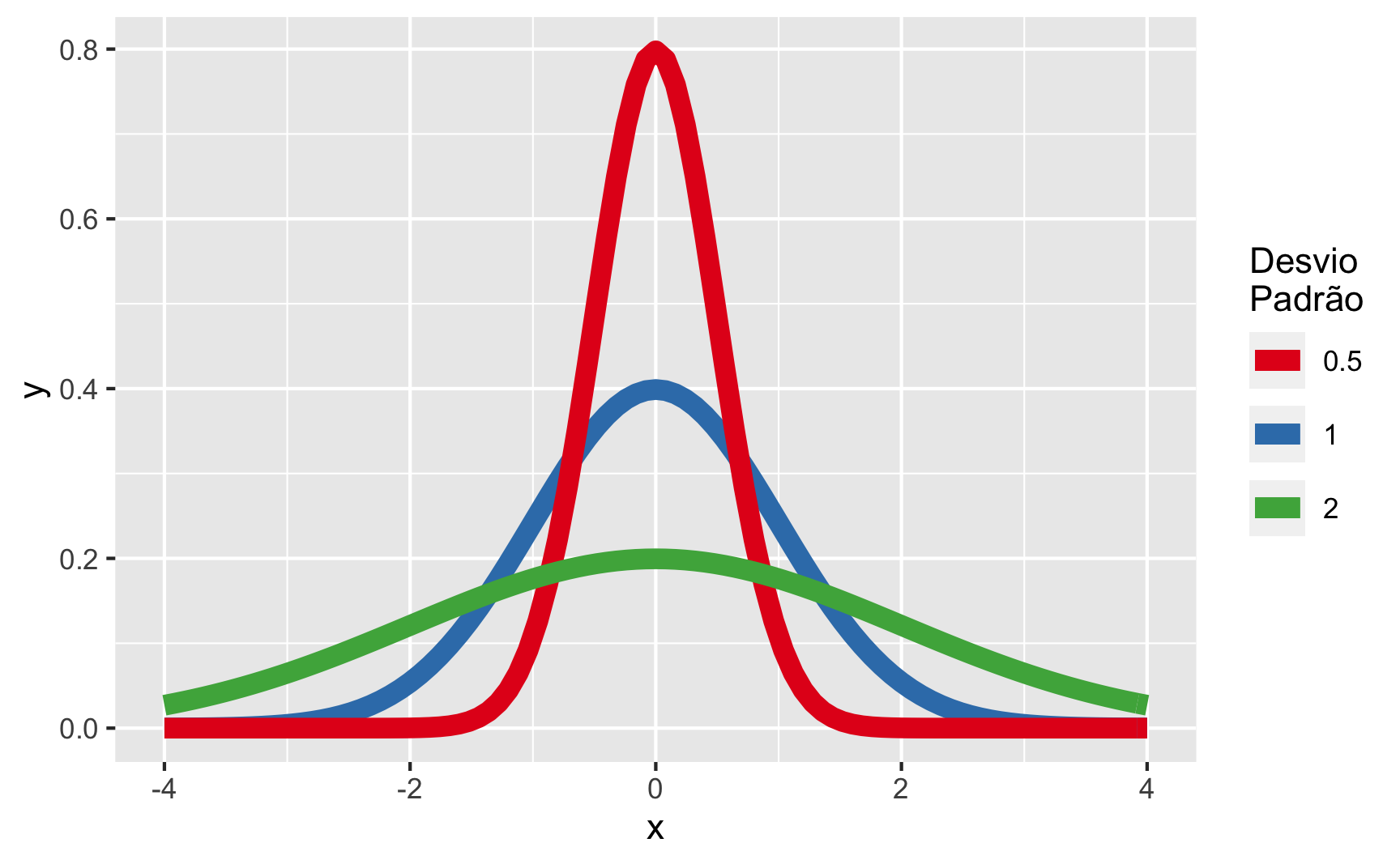
Figure 1: Distribuições Normais com diferentes Desvios Padrões

A correlação mensura o quanto de variação em unidades de desvio padrão duas variáveis estão associadas. Por exemplo, uma correlação de +0.8 indica que conforme \(X\) varia 1 desvio padrão, observa-se uma variação de 0.8 desvio padrão em \(Y\) e vice-versa¹. Na figura 2 é possível visualizar diagramas de dispersão de simulações com 50 observações de diferentes correlações acompanhadas de linhas de tendência em vermelho. No topo de cada diagrama de dispersão é possível ver a magnitude da correlação utilizada na simulação.

correlação <- seq(-1, 1, 0.2)

x <- 1:50
y <- rnorm(50, sd = 10)

complemento <- function(y, correlação, x) {
  y.perp <- residuals(lm(x ~ y))
  correlação * sd(y.perp) * y + y.perp * sd(y) * sqrt(1 - correlação^2)
}

X <- data.frame(z = as.vector(sapply(correlação,
                                     function(correlação) complemento(y, correlação, x))),
                correlação = ordered(rep(signif(correlação, 2),
                                         each = length(y))),
                y = rep(y, length(correlação)))
ggplot(X, aes(y, z, group = correlação)) +
  geom_rug(sides = "b") +
  geom_point(alpha = 0.5) +
  geom_smooth(method = "lm", color = "Red", se = FALSE) +
  facet_wrap(~ correlação, scales = "free", labeller = "label_both", ncol = 4) +
  theme(legend.position = "none")

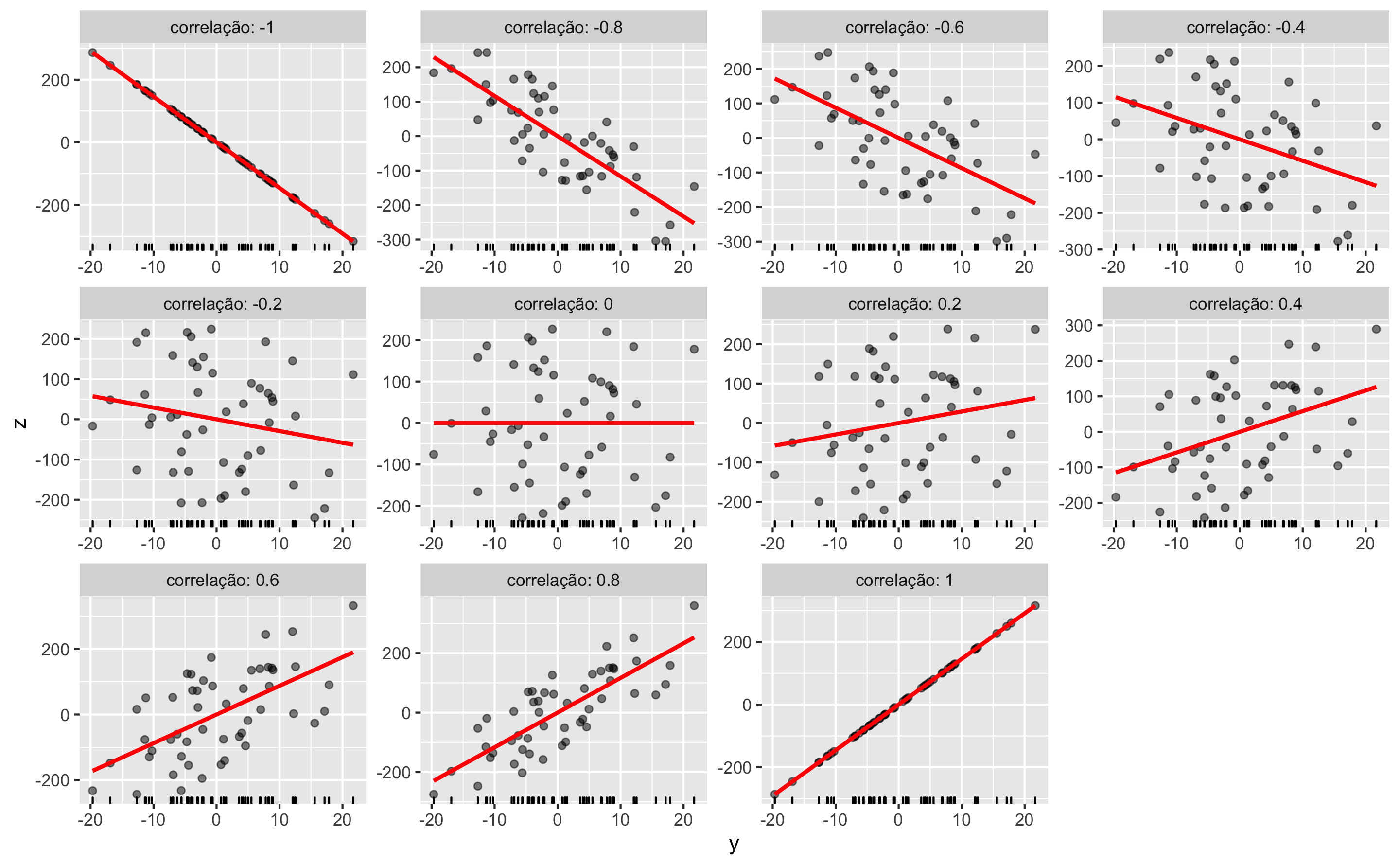
Figure 2: Diagramas de Dispersão com linhas de tendências para as diversas correlações

Pressupostos da Correlação

Correlação deve ser aplicada somente em variáveis contínuas, intervalares ou ordinais. Correlação não podem ser usadas para variáveis nominais (também chamada de categóricas). A lógica por trás desse pressuposto é que magnitudes de associação somente podem ser mensuradas em variáveis que de alguma maneira sejam “mensuráveis e comparáveis numericamente” entre si.

Além disso, as variáveis tem que possuir um critério de linearidade entre elas. Isto quer dizer que quanto mais/menos de x mais/menos de y. Este conceito fica mais claro ao ser visualizado. Na figura 3 é possível ver duas relações entre variáveis x e y: à esquerda, uma relação linear; e à direita, uma relação não-linear.

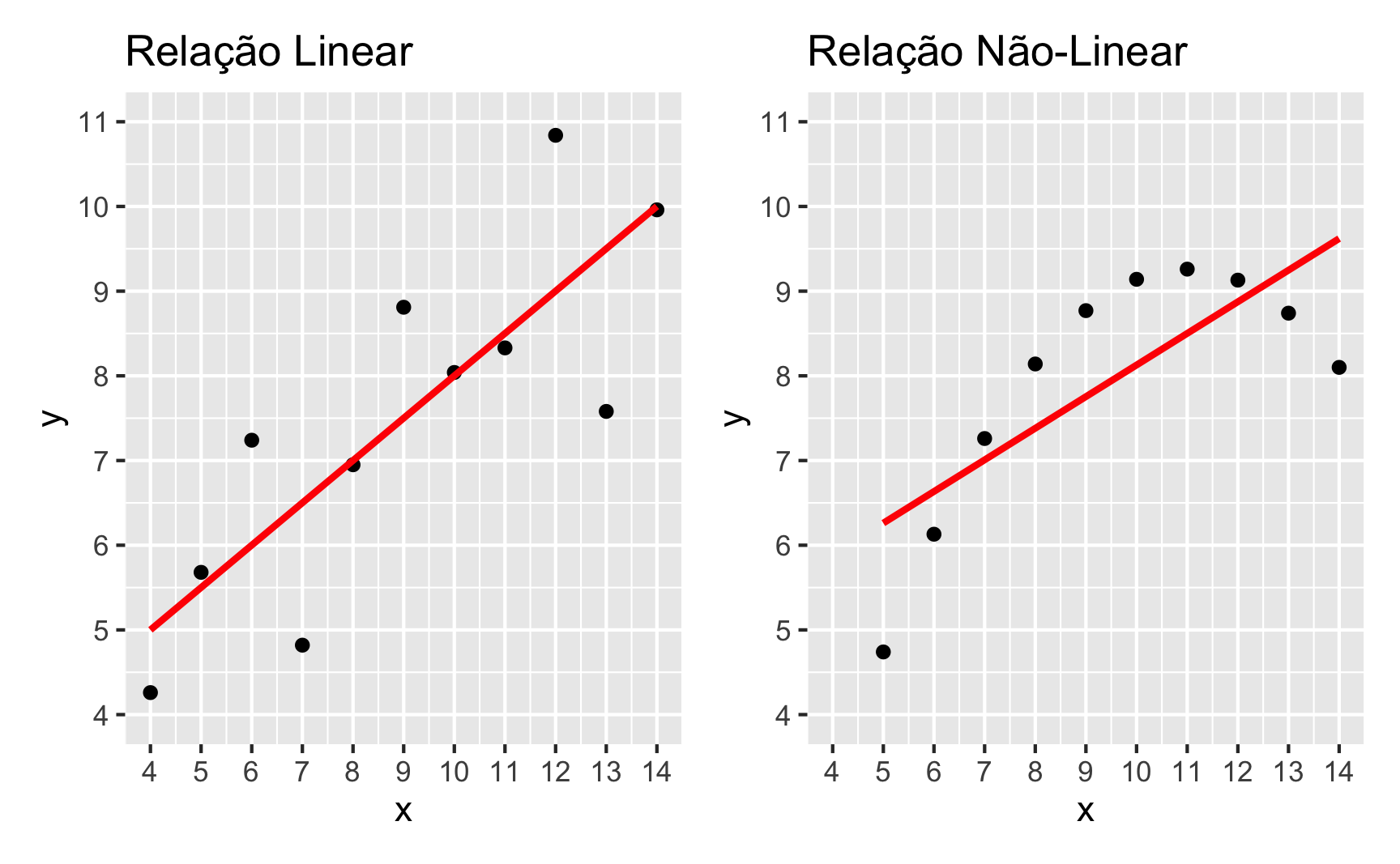
Figure 3: Linearidade vs Não-Linearidade

Tipos de correlação

Até agora todas as correlações que mostramos são correlações de Pearson pois é o tipo de correlação padrão do R. Temos três tipos de correlações que são comumente empregadas:

1. Correlação de Pearson² (Pearson, 1895): a correlação de Pearson é a correlação mais utilizada em análises estatísticas. Ela é uma técnica paramétrica e possui o pressuposto de que ambas as variáveis são distribuídas conforme uma distribuição Normal. Caso tenha dados que violem o pressuposto da normalidade, correlação de Pearson não é o tipo de correlação que você deva usar.
2. Correlação de Spearman³ (Spearman, 1904): a correlação de Spearman é uma técnica não-paramétrica, sendo a alternativa quando os dados violam o pressuposto de normalidade, pois não faz nenhuma suposição que os dados estejam distribuídos de acordo com uma distribuição específica.
3. Correlação de Kendall⁴ (Kendall, 1938): Assim, como a correlação de Spearman, a correlação de Kendall também é uma técnica não-paramétrica. Sendo também uma alternativa viável quando os dados violam o pressuposto de normalidade, pois não faz nenhuma suposição que os dados estejam distribuídos de acordo com uma distribuição específica.

Figure 4: Da esquerda para direita: Karl Pearson, Charles Spearman e Maurice Kendall – Figuras de https://www.wikipedia.org

Quando usar Kendall ou Spearman?

Ambas devem ser usadas quando o pressuposto de normalidade para ambas ou qualquer uma das variáveis que estão sendo correlacionadas for violado.

Sugerimos usar a correlação de Kendall, especialmente quando estamos tratando de amostras pequenas (\(n < 100\)) (Reynolds, 1977). Porém, há alguns cenários que a correlação de Spearman é melhor indicada, conforme Khamis (2008): “Se a variável ordinal, \(Y\), tem um grande número de níveis (digamos, cinco ou seis ou mais), então pode-se usar o coeficiente de correlação de classificação de Spearman para medir a força da associação entre \(X\) e \(Y\)”⁵.

Além disso, as duas divergem em custo computacional. Isto pode ser um critério de decisão caso estejam lidando com um vasto número de observações. O cálculo da correlação de Kendall possui complexidade computacional na ordem de \(O(n^2)\), enquanto que o cálculo da correlação de Spearman possui complexidade computacional na ordem de \(O(n \log n)\), sendo \(n\) o tamanho da amostra.

Como mensurar correlações no R

No R é possível mensurar correlações de duas maneiras:

1. Calculando a medida de correlação entre duas variáveis.
2. Realizando um teste estatístico de hipótese nula sobre a correlação de duas variáveis.

Antes de apresentar os dois métodos, vamos simular⁶ dois cenários de relações bivariadas. O primeiro cenário contém duas distribuições Normais com médias diferentes porém com uma correlação especificada em 0.6. O segundo cenário contém duas distribuições \(t\) de Student⁷ com a mesma correlação especificada em 0.6. Usaremos a biblioteca {mnormt} (Qu, Liu, & Zhang, 2019), que é específica para gerar distribuições multivariadas Normais e não-Normais.

library(mnormt)

medias <- c(0, 10)
covariancias <- matrix(c(1, 0.6, 0.6, 1), 2, 2)

mv_normal <- as.data.frame(rmnorm(50, medias, covariancias))
mv_student <- as.data.frame(rmt(50, medias, covariancias, df = 1))

Para verificar se os pressupostos não serão violados, usaremos o teste de Shapiro-Wilk usando a função shapiro.test() em ambos cenários. Lembrando que a \(H_0\) do teste de Shapiro-Wilk é de que “os dados são distribuídos conforme uma distribuição Normal.”

shapiro.test(mv_normal$V1)

    Shapiro-Wilk normality test

data:  mv_normal$V1
W = 0.97314, p-value = 0.3092

shapiro.test(mv_normal$V2)

    Shapiro-Wilk normality test

data:  mv_normal$V2
W = 0.97163, p-value = 0.2693

Como podem ver, ambos os testes para as distribuições multivariadas Normais geram \(p\)-valores acima de 0.05 o que faz com que falhemos em rejeitar a hipótese nula de que “os dados são distribuídos conforme uma distribuição Normal.”

shapiro.test(mv_student$V1)

    Shapiro-Wilk normality test

data:  mv_student$V1
W = 0.7176, p-value = 1.737e-08

shapiro.test(mv_student$V2)

    Shapiro-Wilk normality test

data:  mv_student$V2
W = 0.4848, p-value = 5.307e-12

Como podem ver, ambos os testes para as distribuições multivariadas \(t\) de Student geram \(p\)-valores abaixo de 0.05 o que faz com que a hipótese nula de que “os dados são distribuídos conforme uma distribuição Normal” é rejeitada.

Calculando a medida de correlação entre duas variáveis

Para calcular a correlação de duas variáveis usamos a função padrão do R cor(). Devemos usar como argumento das duas variáveis que queremos calcular a correlação e como terceiro argumento o tipo de correlação que queremos⁸:

• method = "pearson" – Correlação de Pearson.
• method = "spearman" – Correlação de Spearman.
• method = "kendall" – Correlação de Kendall.

Primeiro cenário, distribuições Normais, técnica paramétrica de correlação de Pearson:

cor(mv_normal$V1, mv_normal$V2, method = "pearson")

[1] 0.6156231

Segundo cenário, distribuições não-Normais, técnica não-paramétrica de correlação de Spearman:

cor(mv_student$V1, mv_student$V2, method = "spearman")

[1] 0.6829772

Segundo cenário, distribuições não-Normais, técnica não-paramétrica de correlação de Kendall:

cor(mv_student$V1, mv_student$V2, method = "kendall")

[1] 0.5036735

Realizando um teste estatístico de hipótese nula sobre a correlação de duas variáveis

Além de computarmos o valor da correlação entre duas variáveis, é possível também realizar um teste estatístico de hipótese nula sobre a correlação de duas variáveis. A hipótese nula \(H_0\) nesse caso é de que “as variáveis possuem correlação igual a zero”.

Para fazermos um teste de hipótese de correlação usamos a função padrão do R cor.test() que funciona similar à cor(). Devemos usar como argumento das duas variáveis que queremos calcular a correlação e como terceiro argumento o tipo de correlação que queremos⁹:

• method = "pearson" – Correlação de Pearson.
• method = "spearman" – Correlação de Spearman.
• method = "kendall" – Correlação de Kendall.

O output de cor.test() inclui um \(p\)-valor, mas somente a correlação de Pearson possui um intervalo de confiança padrão 95% (podendo ser alterado para outras porcentagens caso necessário). Notem que a intuição aqui é que o \(p\)-valor é probabilidade de obter resultados no mínimo tão extremos quanto os que foram observados, dado que a hipótese nula é verdadeira (\(H_0\): correlação entre as variáveis é zero/nula); e o intervalo de confiança expressa a frequência de longo-prazo que você esperaria obter de uma correlação caso replicasse o teste estatístico para diversas amostras da mesma população (nesse caso 95% das amostras de mesmo tamanho que a nossa, \(n = 50\), da mesma população-alvo, aplicando o mesmo teste estatístico de correlação, esperaríamos encontrar uma correlação entre os limites inferiores e superiores do intervalo de confiança).

Primeiro cenário, distribuições Normais, técnica paramétrica de correlação de Pearson:

cor.test(mv_normal$V1, mv_normal$V2, method = "pearson")

    Pearson's product-moment correlation

data:  mv_normal$V1 and mv_normal$V2
t = 5.4124, df = 48, p-value = 1.954e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.4070214 0.7631922
sample estimates:
      cor 
0.6156231 

Note que aqui temos um \(p\)-valor significante e um tamanho de efeito entre 0.4070214 e 0.7631922.

Segundo cenário, distribuições não-Normais, técnica não-paramétrica de correlação de Spearman:

cor.test(mv_student$V1, mv_student$V2, method = "spearman")

    Spearman's rank correlation rho

data:  mv_student$V1 and mv_student$V2
S = 6602, p-value = 1.519e-07
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.6829772 

Aqui também temos um \(p\)-valor significante.

Segundo cenário, distribuições não-Normais, técnica não-paramétrica de correlação de Kendall:

cor.test(mv_student$V1, mv_student$V2, method = "kendall")

    Kendall's rank correlation tau

data:  mv_student$V1 and mv_student$V2
z = 5.1611, p-value = 2.455e-07
alternative hypothesis: true tau is not equal to 0
sample estimates:
      tau 
0.5036735 

Aqui também temos um \(p\)-valor significante.

Paradoxo de Simpson

O paradoxo de Simpson é um fenômeno que surge na análise de dados, que se não for considerado pode levar a conclusões espúrias ou previsões enganosas (Pearl, 2014; Simpson, 1951). A ideia geral do paradoxo é que um conjunto de dados em geral pode parecer uma tendência em uma direção (positiva ou negativa), mas tender na direção oposta quando dividido por subgrupos. Isso é problemático porque olhar para dados agregados pode levar a acreditar que os dados têm uma associação positiva/negativa para todos os grupos, porém ao subdividirmos os dados em subgrupos e analisarmos as associações vemos que a tendência que era positiva/negativa é totalmente revertida.

O paradoxo de Simpson já ocorreu em cenários como: estudo de viés de gênero na entrada de alunos de mestrado e doutorado em UC Berkeley (Bickel, Hammel, & O’Connell, 1975); estudo médico sobre tratamento de pedra de rim (Julious & Mullee, 1994); análise de médias de rebatidas em Baseball (Ross, 2007); análise da disparidade racial em penas de morte (Radelet, 1981); entre outros…

Pinguins de Palmer

Para ilustrar o paradoxo de Simpson, vamos usar o dataset sobre pinguins que foram encontrados próximos da estação de Palmer na Antártica. O dataset pode ser carregado pela biblioteca {palmerpenguins} (Horst, Hill, & Gorman, 2020). Nós, sempre que carregamos um dataset no R, temos o costume de usar a biblioteca {skimr} (Waring et al., 2020) para produzir um sumário dos dados.

library(magrittr)
library(palmerpenguins)
library(skimr)
penguins <- penguins %>% na.omit()
skim(penguins)

Table 1: Data summary

Name	penguins
Number of rows	333
Number of columns	8
_______________________
Column type frequency:
factor	3
numeric	5
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
species	0	1	FALSE	3	Ade: 146, Gen: 119, Chi: 68
island	0	1	FALSE	3	Bis: 163, Dre: 123, Tor: 47
sex	0	1	FALSE	2	mal: 168, fem: 165

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
bill_length_mm	0	1	43.99	5.47	32.1	39.5	44.5	48.6	59.6	▃▇▇▆▁
bill_depth_mm	0	1	17.16	1.97	13.1	15.6	17.3	18.7	21.5	▅▆▇▇▂
flipper_length_mm	0	1	200.97	14.02	172.0	190.0	197.0	213.0	231.0	▂▇▃▅▃
body_mass_g	0	1	4207.06	805.22	2700.0	3550.0	4050.0	4775.0	6300.0	▃▇▅▃▂
year	0	1	2008.04	0.81	2007.0	2007.0	2008.0	2009.0	2009.0	▇▁▇▁▇

Como vocês podem verificar, temos observações de três espécies de pinguins:

• Adelie – 146 observações.
• Chinstrap – 68 observações.
• Gentoo – 119 observações.

Na figura 5 é possível observar duas ilustrações: à esquerda as três diferentes espécies de pinguins observadas no dataset e à direita ilustrando o significado das variáveis comprimento de bico bill_length_mm e altura de bicobill_depth_mm.

Figure 5: Da esquerda para direita: as diferentes espécies de pinguins Palmer e ilustração do bico do pinguim – Figuras de https://allisonhorst.github.io/palmerpenguins

Dados agregados

Para iniciar a exemplificação do paradoxo de Simpson, mostraremos os dados agregados da associação entre o comprimento do bico bill_length_mm e a altura do bico bill_depth_mm dos pinguins, ambos mensurados em milímetros e independente de espécie. Na figura 6 é possível ver um diagrama de dispersão do comprimento e altura dos bicos dos pinguins, independente de espécie, e com uma linha de tendência em azul. A correlação, por esse gráfico de dispersão, mostra uma associação negativa entre comprimento e altura do bico. E, agora, perguntamos: isto faz sentido? Vocês acreditam que essa associação é realmente negativa: quanto maior o comprimento do bico menor a altura do bico?

penguins %>%
  ggplot(aes(bill_length_mm, bill_depth_mm)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, size = 2)  +
  labs(x = "comprimento do bico",
       y = "altura do bico",
       caption = "dados agregados")

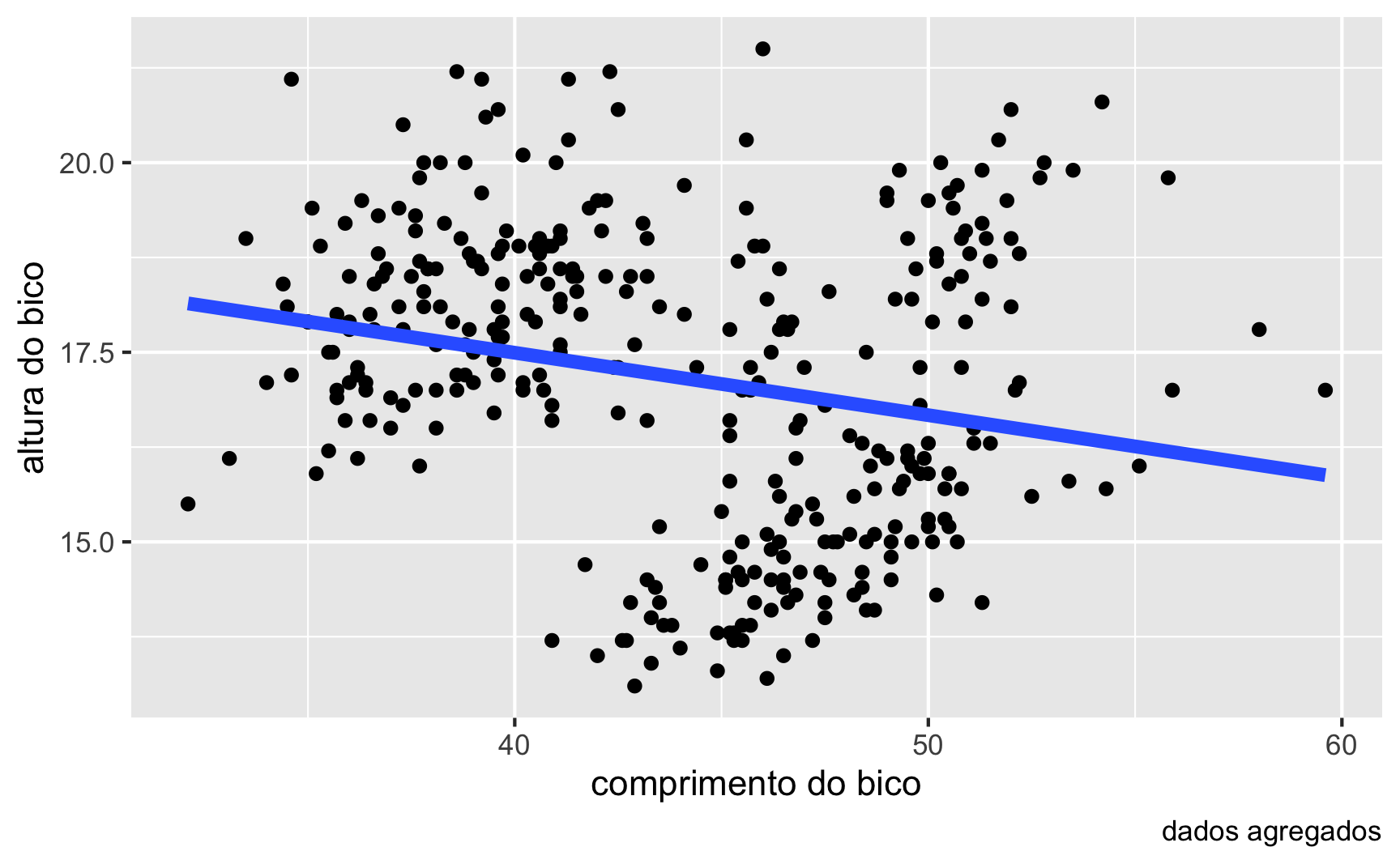
Figure 6: Diagrama de dispersão agregado do comprimento e altura dos bicos dos pinguins

Veja o que acontece quando dividimos os dados por subgrupos (no caso espécies). Na figura 7 é possível ver um diagrama de dispersão do comprimento e altura dos bicos dos pinguins, subdividos em espécie por cor, e com uma linha de tendência na cor de cada espécie. A correlação, por esse gráfico de dispersão, mostra uma associação positiva entre comprimento e altura do bico quando consideramos espécie.

penguins %>%
  ggplot(aes(bill_length_mm, bill_depth_mm, color = species)) +
  geom_point() +
  geom_smooth(aes(group = species), method = "lm", se = FALSE, size = 2)  +
  labs(x = "comprimento do bico",
       y = "altura do bico",
       caption = "dados subdividos por espécie") +
  scale_color_brewer("Espécie", palette = "Set1") +
  theme(legend.position = "bottom")

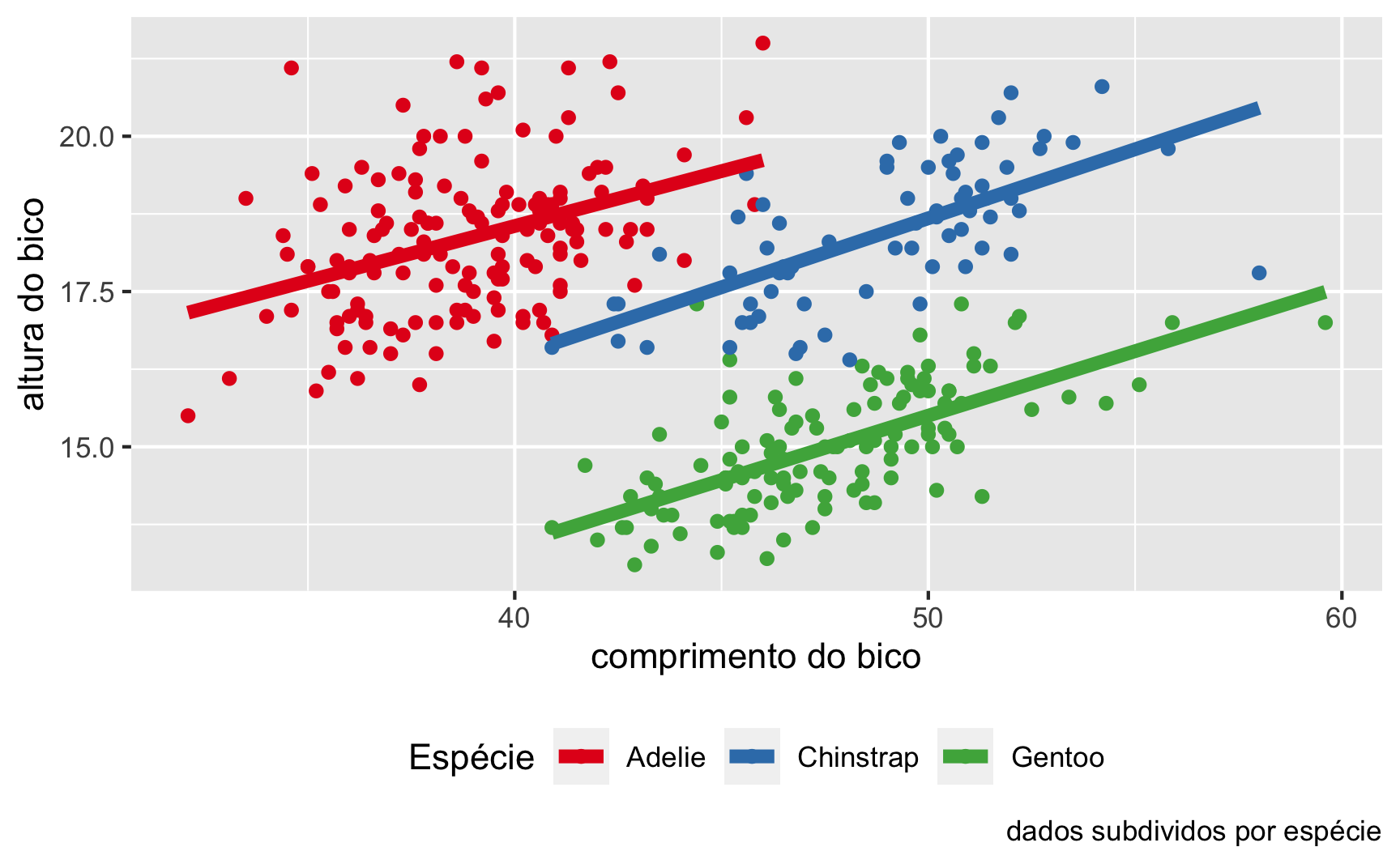
Figure 7: Diagrama de dispersão subdividido em espécies do comprimento e altura dos bicos dos pinguins

Comentários Finais

A correlação é uma métrica extremamente útil para quantificar a magnitude de associação entre duas variáveis. Porém, são necessários alguns cuidados.

Sobre as técnicas de correlação em si, precisamos estar atentos a quais tipos de dados que temos. Caso as variáveis que desejamos correlacionar possuam uma distribuição similar à distribuição Normal (teste de Shapiro-Wilk com \(p\)-valor acima de 0.05) podemos usar a correlação de Pearson; caso contrário teremos que usar uma técnica de correlação não-paramétrica e escolher entre correlação de Spearman ou correlação de Kendall.

Sobre a interpretação das correlações e associações, não se esqueça do mantra da tutorial 2 sobre \(p\)-valores: “correlação não é causalidade.” Além disso, se atentem ao paradoxo de Simpson, especialmente quando estiverem com dados que podem ser subdividos em grupos.

Caso tenha sido intrigado pelo paradoxo de Simpson, não deixe de olhar o nosso conteúdo auxiliar sobre o quarteto de Anscombe.

Ambiente

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.7

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] palmerpenguins_0.1.0 magrittr_2.0.1       mnormt_2.0.2        
 [4] cowplot_1.1.1        tidyr_1.1.2          DescTools_0.99.40   
 [7] skimr_2.1.2          ggpubr_0.4.0         car_3.0-10          
[10] carData_3.0-4        patchwork_1.1.1      dplyr_1.0.4         
[13] ggplot2_3.3.3        DiagrammeR_1.0.6.1   readxl_1.3.1        

loaded via a namespace (and not attached):
 [1] nlme_3.1-149       lubridate_1.7.9.2  RColorBrewer_1.1-2
 [4] rprojroot_2.0.2    ggsci_2.9          repr_1.1.3        
 [7] tools_4.0.3        backports_1.2.1    utf8_1.1.4        
[10] R6_2.5.0           mgcv_1.8-33        DBI_1.1.1         
[13] colorspace_2.0-0   withr_2.4.1        tidyselect_1.1.0  
[16] Exact_2.1          downlit_0.2.1      curl_4.3          
[19] compiler_4.0.3     cli_2.3.0          expm_0.999-6      
[22] xml2_1.3.2         labeling_0.4.2     bookdown_0.21     
[25] scales_1.1.1       mvtnorm_1.1-1      stringr_1.4.0     
[28] digest_0.6.27      foreign_0.8-80     rmarkdown_2.6     
[31] rio_0.5.16         base64enc_0.1-3    pkgconfig_2.0.3   
[34] htmltools_0.5.1.1  highr_0.8          htmlwidgets_1.5.3 
[37] rlang_0.4.10       rstudioapi_0.13    visNetwork_2.0.9  
[40] farver_2.0.3       generics_0.1.0     jsonlite_1.7.2    
[43] zip_2.1.1          distill_1.2        Matrix_1.2-18     
[46] Rcpp_1.0.6         munsell_0.5.0      fansi_0.4.2       
[49] abind_1.4-5        reticulate_1.18    lifecycle_0.2.0   
[52] stringi_1.5.3      yaml_2.2.1         rootSolve_1.8.2.1 
[55] MASS_7.3-53        grid_4.0.3         forcats_0.5.1     
[58] crayon_1.4.1       lmom_2.8           lattice_0.20-41   
[61] splines_4.0.3      haven_2.3.1        hms_1.0.0         
[64] tmvnsim_1.0-2      magick_2.6.0       knitr_1.31        
[67] pillar_1.4.7       boot_1.3-25        gld_2.6.2         
[70] ggsignif_0.6.0     glue_1.4.2         evaluate_0.14     
[73] data.table_1.13.6  vctrs_0.3.6        cellranger_1.1.0  
[76] gtable_0.3.0       purrr_0.3.4        assertthat_0.2.1  
[79] xfun_0.21          openxlsx_4.2.3     broom_0.7.4       
[82] e1071_1.7-4        rstatix_0.6.0      class_7.3-17      
[85] tibble_3.0.6       ellipsis_0.3.1    

---

1. correlação é uma medida simétrica↩︎

2. também chamado de \(r\) de Pearson↩︎

3. também chamado de \(\rho\) (letra grega rho) de Spearman↩︎

4. também chamado de \(\tau\) (letra grega tau) de Kendall↩︎

5. original em inglês: If the ordinal variable, \(Y\), has a large number of levels (say, five or six or more), then one may use the Spearman rank correlation coefficient to measure the strength of association between \(X\) and \(Y\).↩︎

6. sim, adoramos simulações, como vocês já devem ter percebido.↩︎

7. estamos especificando 1 grau de liberdade↩︎

8. esse argumento é opcional e caso não seja especificado cor() usará como padrão method = "pearson"↩︎

9. esse argumento é opcional e caso não seja especificado cor.test() usará como padrão method = "pearson"↩︎